Графический метод решения задач с параметрами
реклама

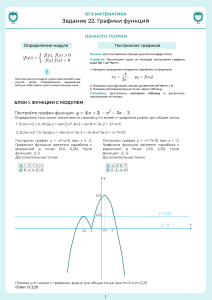
Разбор и решение заданий №23 из сборника типовых тестовых заданий для подготовки к ГИА 2013 под ред. И.В.Ященко Презентация учителя математики МБОУ Щелковская гимназия, 1 Хачунц Гайи Григорьевны Семейство прямых, параллельных оси ОХ î áù èé âèä у=с 3 Семейство прямых, проходящих через начало координат î áù èé âèä у kx 4 5 №23. Вариант 1(3) 6 Рассмотрим два случая: Таким образом, исходная функция есть кусочно-квадратичная 7 График - парабола, ветви которой направлены вверх. Основные точки найдем по таблице 4 2 8 х 2 , если 0 х 2 у 2 х , если х 0 x 0 1 2 3 y 0 1 4 9 y x 2 , если x 0 4 -2 -1 2 -1 -4 9 Определим, при каких значениях с прямая у=с не имеет с графиком ни одной общей точки Нет общих точек 4 Одна общая точка -2 -1 2 -1 Одна общая точка -4 Ответ: при с 4 прямая у с не имеет с графиком функции x -2х x у 2 x2 Однаточки общая точка ни одной общей 10 №23. Вариант 2 (9) 11 Алгебраический метод Найдем, Чтобы полученное при каких значениях квадратное уравнение параметра к уравнение имелоимеет один корень, х2+4=кх один корень. необходимо выполнение Это и будетD=0. искомым условия значением к x 2 4 kx x 2 kx 4 0 D 0 k 2 16 0 k 4 Итак, получены два значения к. Построим параболу у=х2+4 и прямые у=4х и у= - 4х 12 у=х2+4 - парабола у=х2, смещенная на у=4х 4 масштабных Проведем прямые и у=-4х единицы вверх вдоль оси ОУ -2 2 Ответ: при k 4 прямая у kx имеет с графиком функции у х 2 4 ровно одну общую точку 13 Графический метод Примечание: При решении данной задачи графическим методом может создаться ложное впечатление, что таких прямых гораздо больше. 14 Проведем множество прямых вида у=кх -2 2 Выберем среди прямых те, которые имеют одну общую точку с графиком функции у=х2+4 15 При изменении масштаба видно, что «подозрительные» точки не удовлетворяют условию задачи 16 у=- 4х у=4х Ответ: при k 4 прямая у kx имеет с графиком функции у х 2 4 ровно одну общую точку 17 №23. Вариант 4(10) 18 19 20 Определим, при каких значениях с прямая у=с имеет с графиком ровно две общие точки 21 Обобщим полученные результаты 1 общая точка 9 2 общие точки 3 общие точки -7 2 общие точки 1 общая точка 22 Ответ: при с=-7 и с=9 прямая у=с имеет с графиком функции ровно две общие точки 23 №23. Вариант 5 (7) 24 25 Определим, при каких значениях b прямая у=b имеет с графиком ровно одну общую точку 1 общая точка 4 Ответ: при b=0; 4 прямая у=b имеет с графиком ровно одну общую точку 26 №23. Вариант 6(8) 27 -2 28 Проведем множество прямых вида у=кх -2 2 Выберем среди прямых те, которые имеют одну общую точку с графиком функции у=1/х 29 Проверим алгебраически, является ли точка А(-1; -1) Напишем уравнение прямой у=кх,прямой проходящей точку А(-1;-1) единственной общей точкой у= х и через гиперболы у=1/х А(-1;-1) Ответ: при к=1 прямая у=кх имеет с графиком функции ровно одну общую точку 30 31