MS PowerPoint, 1,51 Мб
реклама
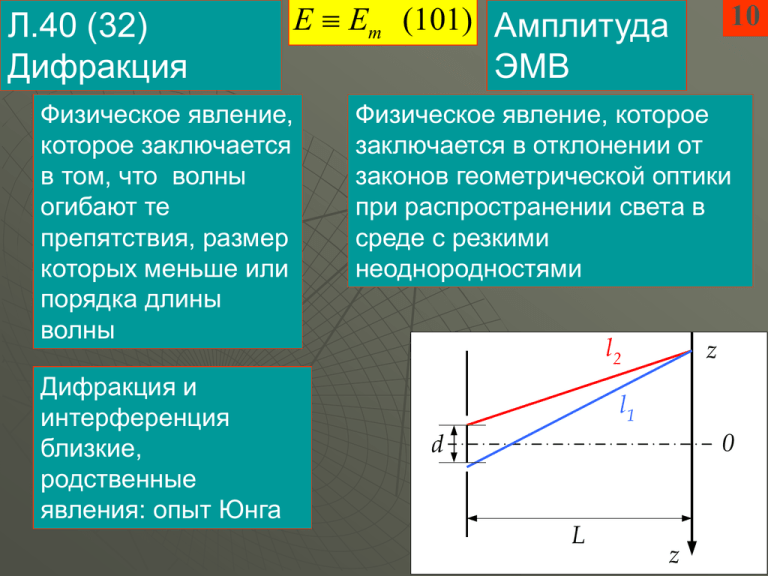
Л.40 (32) Дифракция E Em (101) Амплитуда Физическое явление, которое заключается в том, что волны огибают те препятствия, размер которых меньше или порядка длины волны Дифракция и интерференция близкие, родственные явления: опыт Юнга 10 ЭМВ Физическое явление, которое заключается в отклонении от законов геометрической оптики при распространении света в среде с резкими неоднородностями l2 z l1 0 d L z 11. Дифракция волн. Типичная дифракционная картина. b2 /(l ) 1 Дифракция Френеля b2 /(l ) 1 b /(l ) 1 2 Дифракция Фраунгофера 20 Свойства волн (волновые явления): Дифракция b Нет дифракции – геометрическая оптика b Есть дифракция Огибание волнами препятствий, размер которых меньше или порядка длины волны 30 Работал инженером по ремонту 35 и строительству дорог – дороги во Франции хорошие… Участник боевых действий (Наполеон) Физику изучил самостоятельно!!! Принцип Гюйгенса-Френеля Огюстен Жан Френель (1788-1827) Вся волновая оптика. Образование: Политехническая школа (1806), Школа мостов и дорог (1809) Теория интерференции и дифракции света Формулы Френеля – поляризация света при отражении Зеркала и бипризма Френеля 36 Фонари для маяков, в которых свет усиливается линзами Френеля 37 Молодой дорожный инженер Огюстен Френель (1788—1827), присоединившийся волонтером к роялистским войскам, которые должны были преградить дорогу Наполеону во время его возвращения с острова Эльба, в период Ста дней был уволен со службы и вынужден был удалиться в Матье, близ Казна. Молодой инженер, почти не сведущий в оптике, находясь в Казне, посвятил себя исследованию дифракции, имея в своем распоряжении лишь случайное и примитивное экспериментальное оборудование. Два мемуара, представленных им 15 октября 1815 г. Парижской Академии наук, были первым результатом этих трудов. Араго, которому вместе с Пуаcсоном поручили рассмотреть их и прореферировать, нашел их настолько интересными, что добился для Френеля, который с наступлением реставрации был вновь принят на службу, приглашения в Париж для повторения своих опытов в более благоприятных условиях. (Mathieu, Caen) Открыл спектральные линии в солнечном излучении 38 Впервые применил дифракционную решётку для измерения длин волн спектральных линий Работал в Мюнхене (тогда Королевство Бавария) Йозеф Фраунгофер (1787-1826) Подмастерье и мастер в стекольной и зеркальной мастерской. Образование: математическое самообразование 40 Расчёт распределения интенсивности в дифракционной картине: метод зон Френеля l1 lm Em+1 +Em-1 Em (402) 2 screen E E0 E1 +E2 E3 +... (401) lm ml1l2 rm (403) l1 l2 l2 m l1l2 l1 l2 (404) Метод зон Френеля: открыта одна зона E E0 (501) I I 0 (502) l1 I l2 z 50 60 Метод зон Френеля: открыто две зоны E E0 E1 (601) E0 E0 E2 E2 E E1 + (602) 2 2 2 2 l1 I l2 I0 I (603) 4 z Парадоксы теории Френеля: если закрыть - за экраном светло, если открыть – напротив отверстия темно 65 70 Метод зон Френеля: все зоны открыты E E0 E1 +E2 E3 +... (701) l1 lm screen E0 E0 E2 E2 E4 E E1 + E3 +... (702) 2 2 2 2 2 lm l2 Это в 4 раза меньше, чем если открыта одна зона! I0 I (703) 4 80 Метод зон Френеля: пятно Пуассона Em E 2 Em2 Em2 Em4 Em Em1 + Em3 + +... (801) 2 2 2 2 l1 c 0 E I 2 I 2 (802) Im I (803) 4 l2 z 85 Дифракция Фраунгофера на щели 2m 1 (852) 2 b sin max sin b / sin I ( ) I 0 (851) b / sin 2 0 I b b sin min L (853) z 2m 2 90 Дифракционная решётка sin b / sin I Э ( ) I 0 b / sin d sin max m (902) 2 sin N d / sin sin d / sin 2 (901) Фазированная антенная решётка 93 Дифракция ограничивает разрешающую способность оптических приборов 95


![Контроль успеваемости [DOC, 47 КБ]](http://s1.studylib.ru/store/data/000237842_1-2b5bdb1a697aa000b70cced7d1cb16d0-300x300.png)




