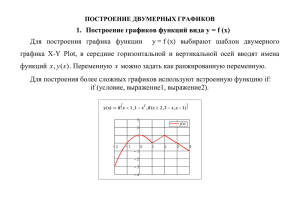
Построить график функции с помощью элементарных

Математика
Построить график функции с помощью элементарных
преобразований графика квадратичной функции
1)
у  х  2х
2)
у  х 2х
3)
1
у 2
1
х 6х 8
2
2
Научно-практическая конференция учащихся Псковской области
«Шаг в будущее»
11 – 13 декабря 2013 года, г. Псков
Построение графиков функций с
помощью
элементарных преобразований.
Шашнев Павел Андреевич
11-а класс
МАОУ «Гуманитарный лицей»
Г. Псков.
Цель исследовательской работы:
Изучение и применение основных
методов построения графиков сложных
функций, как один из факторов развития
исследовательской культуры, а также
расширение представления о
возможном использовании известных
сведений (свойств объектов) в новых
ситуациях.
Поставлены задачи:
1. Изучить теоретические сведения для построения графиков
функций , методы построения графиков сложных функций.
2. Научиться строить графики функций с помощью элементарных
преобразований (без применения производной). В частности:
у  2 х 1
3.
2х 2  х  1
у 2
2х  х  1
х2  х 1
у 2
х  х 1
у
1
х2  6 х  8
Развить культуру построения графических образов.
4. Готовиться к ЕГЭ по математике в процессе исследовательской
деятельности.
В работе рассмотрены:
Часть 1. Методы построения графиков функций
•Преобразования, сводящиеся к линейным.
•Преобразования, не сохраняющие линейность.
•Поведение функции вблизи точек разрыва и в бесконечности.
Асимптоты функции.
Часть 2. Практическое применение методов построения
графиков функций.
В учебнике М. Я. Пратусевича приводится
разделение элементарных преобразований на
линейные и не сохраняющие линейность (стр.
201-203)
Часть 1.Методы построения графиков функций
Преобразования, сводящиеся к линейным.
y = f(x) + a где а  R
Преобразования, сводящиеся к линейным.
y = f(x + a)
где a ϵ R
y = a f(x) где a>0
y = f(ax)
Преобразования, сводящиеся к линейным.
где a>0
y = - f(x)
Преобразования, сводящиеся к линейным.
y = f( - x)
y = | f(x) |
Преобразования, сводящиеся к линейным.
y = f( | x | )
Преобразования не сохраняющие линейность
1
у
f ( x)
Пример. Построим график
функции примере функции у 
1
2х 2  4х
Рекомендации для построения:
1.Отметить точки пересечения f(x) c
1
осью Ох. В этих точках функция у  f ( x)
не определена.
2. Провести вертикальные прямые через эти точки ( на них не лежит ни
одной точки графика )
3. Эти прямые разбивают плоскость на полосы; далее мы будем
рассматривать все полосы по отдельности и строить части графика функции
1
, попавшие внутрь такой полосы.
у
f ( x)
4.
Отметить точки пересечения
графика f(x) с прямыми
y=1 и y=-1. Они останутся на графике
функции у  1
f ( x)
5. В каждой полосе, ограниченной
прямыми , построить часть графика
функции у  1
f ( x)
попавшего внутрь этой полосы, двигаясь от неподвижной точки( если она здесь) к
границам полосы. Образы этой куска кривой будет заключен внутри этой же полосы.
Поведение функции вблизи точек разрыва и в бесконечности. Асимптоты
функции.
Напомню, что существует три вида
асимптот:
•вертикальные
•наклонные
•горизонтальные
Часть 2. Практическое применение методов построения графиков
функций
Часто бывает полезно уметь построить эскиз графика функции,
например, для решения задач С5 в ЕГЭ. Например:
№1. При каких значениях параметра а уравнение
имеет три решения?
х 2  16 х  а( х  9)
ах 2  х  1  0
Задача.
Построить с помощью
элементарных преобразований график
х2  х 1
функции у  2
х  х 1
Приведём функцию к виду
С помощью элементарных преобразований функции x+1/x легко
построить график
2) f(x) -1
1) f(x)
3)
4)
Интересно, что при похожести задания
2х  х  1
функции
у
2
2х 2  х  1
графики у них получаются разные
из-за
появления
вертикальных
асимптот x= -1/2 и x=1.
у
2х 2  х  1
2х 2  х  1
у
х2  х 1
х2  х 1
Список литературы и интернет-источников.
1.
Н.А. Бирченко, И.И. Ляшко, К.И. Шведов «Графики функций.
Справочник». Издательство Киев «НАУКОВА ДУМКА» 1979 г.
2. С.М. Никольский, Н.Н. Решетников учебник «Алгебра и начала
анализа» Москва «Просвещение» 2003 г. стр. 448
3.М.Я. Пратусевич « Алгебра и начала математического анализа».
Профильный уровень. Москва «Просвещение» 2009г.
4. И.Я. Танатор «Геометрические преобразования
функций» УЧПЕДГИЗ – 1960 г. стр. 168
5. graficus.ru
6.mathprofi.ru
графиков