В4 Системы счисления и двоичное представление информации в памяти компьютера.

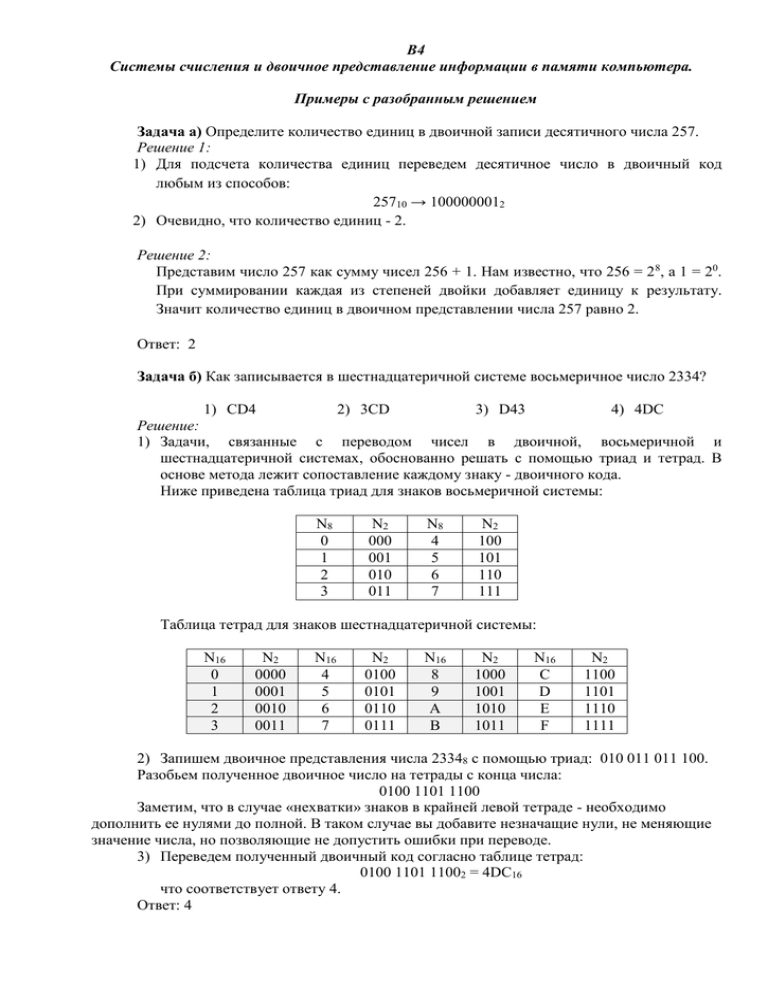
В4
Системы счисления и двоичное представление информации в памяти компьютера.
Примеры с разобранным решением
Задача а) Определите количество единиц в двоичной записи десятичного числа 257.
Решение 1:
1) Для подсчета количества единиц переведем десятичное число в двоичный код
любым из способов:
25710 → 1000000012
2) Очевидно, что количество единиц - 2.
Решение 2:
Представим число 257 как сумму чисел 256 + 1. Нам известно, что 256 = 2 8, а 1 = 20.
При суммировании каждая из степеней двойки добавляет единицу к результату.
Значит количество единиц в двоичном представлении числа 257 равно 2.
Ответ: 2
Задача б) Как записывается в шестнадцатеричной системе восьмеричное число 2334?
1) CD4
2) 3CD
3) D43
4) 4DC
Решение:
1) Задачи, связанные с переводом чисел в двоичной, восьмеричной и
шестнадцатеричной системах, обоснованно решать с помощью триад и тетрад. В
основе метода лежит сопоставление каждому знаку - двоичного кода.
Ниже приведена таблица триад для знаков восьмеричной системы:
N8
0
1
2
3
N2
000
001
010
011
N8
4
5
6
7
N2
100
101
110
111
Таблица тетрад для знаков шестнадцатеричной системы:
N16
0
1
2
3
N2
0000
0001
0010
0011
N16
4
5
6
7
N2
0100
0101
0110
0111
N16
8
9
А
B
N2
1000
1001
1010
1011
N16
C
D
E
F
N2
1100
1101
1110
1111
2) Запишем двоичное представления числа 23348 с помощью триад: 010 011 011 100.
Разобьем полученное двоичное число на тетрады с конца числа:
0100 1101 1100
Заметим, что в случае «нехватки» знаков в крайней левой тетраде - необходимо
дополнить ее нулями до полной. В таком случае вы добавите незначащие нули, не меняющие
значение числа, но позволяющие не допустить ошибки при переводе.
3) Переведем полученный двоичный код согласно таблице тетрад:
0100 1101 11002 = 4DC16
что соответствует ответу 4.
Ответ: 4
Задача в) Дано: x8 = 434, y10 = 286. Какое из чисел z, записанных в десятичной системе
счисления, удовлетворяет неравенству x < z < y?
1) 101111101
2) 100011101
3) 100011110
4) 111111101
Решение:
1) Поскольку одно из чисел десятичное, целесообразно перевести все сравниваемые
числа либо в двоичную, либо в десятичную систему. Причем проще и быстрее
перевести всё в двоичный код.
2) При переводе 4348 воспользуемся таблицами триад. Получим 1000111002.
3) При переводе 28610 воспользуемся любым методом перевода. Получим 1000111102.
4) Очевидно, что единственное двоичное число, удовлетворяющее неравенству
x < z < y это 100011101
Ответ: 2
Задача г) Для хранения в памяти компьютера целого числа со знаком используется
один байт. Сколько единиц содержит внутреннее представление числа (-66)?
1) 2
2) 7
3) 6
4) 3
Решение:
1) Решение задачи предполагает знания учащимися перевода в двоичный код
отрицательных чисел.
2) Переведем в двоичную систему положительное число 66. Получим 10000102.
Поскольку в задаче сказано, что число храниться в одном байте, значит необходимо
дополнить код до длины в 8 бит (8 разрядов). Дополняем незначащими нулями
слева: 010000102. Теперь код имеет длину 8 бит или 1 байт.
3) Производим инверсию знаков (меняем ноль на единицу и единицу на ноль).
Получаем: 101111012. Добавляем единицу к результату. Получаем: 101111102.
Количество единиц в полученном коде - 6.
4) При сложении двоичного числа с единицей, пожалуйста, аккуратно выполняйте
переносы при переполнении разрядов.
Ответ: 3
Задача д) Найдите наибольшее трехзначное число, двоичное представление которого
содержит 3 единицы (остальные цифры нули).
Решение:
1) Безусловно, наибольшее трехзначное десятичное число это 999. Переведем его в
двоичный код и получим 11111001112.
2) В получившемся числе 8 единиц, значит нам нужно заменить 5 единиц на нули,
чтобы выполнить условие задачи. Для того чтобы получившееся число было
наибольшим, замену единиц следует производить в младших разрядах. Всего в
числе 10 разрядов - это нужно помнить.
3) Оставим единицы только в старших разрядах: 11100000002.
4) Переведем полученное число в десятичное. Получим 896.
5) Пожалуйста помните, что при решении задач на нахождение наименьшего числа
алгоритм размышлений будет другим.
Ответ: 896
Задания для самостоятельного решения
1) Определите количество значащих нулей в двоичной записи десятичного числа 485.
Ответ: 3
2) Определите количество единиц в двоичной записи десятичного числа 372.
Ответ: 6
3) Определите количество значащих нулей в двоичной записи шестнадцатеричного числа
А916.
Ответ: 4
4) Определите количество единиц в двоичной записи восьмеричного числа 2148.
Ответ: 3
5) Определите количество единиц в двоичной записи десятичного числа 129.
Ответ: 2
6) Определите количество единиц в двоичной записи десятичного числа 515.
Ответ: 2
7) Как записывается в двоичной системе десятичное число 324?
1) 101110100
2) 101000111
3) 101000100
4) 100000101
Ответ: 3
8) Как записывается в двоичной системе шестнадцатеричное число D3?
1) 10010001
2) 11010011
3) 11110011
4) 10000011
Ответ: 2
9) Как записывается в восьмеричной системе шестнадцатеричное число С3A?
1) 6073
2) 5472
3) 6052
4) 6072
Ответ: 4
10) Как записывается в шестнадцатеричной системе десятичное число 800?
1) 320
2) 230
3) 302
4) 200
Ответ: 1
11) Дано: a16 = C6, b8 = 308. Какое из чисел c, записанных в двоичной системе счисления,
удовлетворяет неравенству a < c < b?
1) 11011001
Ответ: 3
2) 11010011
3) 11000111
4) 10010011
12) Дано: x10 = 150, y8 = 228. Какое из чисел z, записанных в двоичной системе счисления,
удовлетворяет неравенству x < z < y?
1) 11011001
2) 10010111
3) 11000001
4) 10010011
Ответ: 2
13) Дано: a2 = 10101001, b16 = В0. Какое из чисел с, записанных в восьмеричной системе
счисления, удовлетворяет неравенству a < c < b?
1) 2518
2) 2508
3) 2528
4) 2558
Ответ: 1
14) Дано: n2 = 10111011, m10 = 189. Какое из чисел f, записанных в шестнадцатеричной
системе счисления, удовлетворяет неравенству n < f < m?
1) ВA16
2) AB16
3) ВС16
4) BE16
Ответ: 3
15) Дано: n2 = 10001010, m2 = 10001110. Какое из чисел f, записанных в десятичной системе
счисления, удовлетворяет неравенству n < f < m?
1) 146
2) 144
3) 136
4) 140
Ответ: 4
16) Для хранения в памяти компьютера целого числа со знаком используется один байт.
Сколько единиц содержит внутреннее представление числа (-25)?
5) 5
6) 6
7) 2
8) 3
Ответ: 2
17) Для хранения в памяти компьютера целого числа со знаком используется один байт.
Сколько значащих нулей содержит внутреннее представление числа (-113)?
1) 3
2) 2
3) 4
4) 5
Ответ: 1
18) Найдите наименьшее число:
1) ВA16
2) 18810
3) 2708
4) 101110012
3) 6С16
4) 1558
Ответ: 3
19) Найдите наибольшее число:
1) 11010
Ответ: 1
2) 11010112
20) Найдите то число, двоичное представление которого содержит 5 единиц (остальные
цифры нули):
1) С416
2) 23010
3) F016
4) 2378
Ответ: 2
21) Найдите то число, двоичное представление которого содержит 3 значащих нуля
(остальные цифры единицы):
1) 19010
2) 1478
3) 2428
4) F216
Ответ: 4
22) Найдите то число, двоичное представление которого содержит 4 единицы (остальные
цифры нули). Если таких чисел несколько, найдите наибольшее:
1) 15110 + 28
2) 9B16 + 1010
3) 2628
4) 22010
Ответ: 3
23) Найдите то число, двоичное представление которого содержит 3 единицы (остальные
цифры нули). Если таких чисел несколько, найдите наименьшее:
1) 1578 + 116
2) 2548
3) 13610 + 816*28
4) A816
Ответ: 1
24) Найдите наибольшее трехзначное восьмеричное число, двоичное представление
которого содержит 5 единиц (остальные цифры нули).
Ответ: 760
25) Найдите наименьшее четырехзначное десятичное число, двоичное представление
которого содержит 4 единицы (остальные цифры нули).
Ответ: 1031
26) Найдите наименьшее двузначное шестнадцатеричное число, двоичное представление
которого содержит 3 единицы (остальные цифры нули).
Ответ: 13