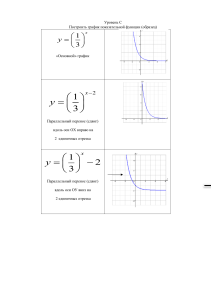
«П » РЕОБРАЗОВАНИЕ ГРАФИКА

«ПРЕОБРАЗОВАНИЕ
ГРАФИКА
КВАДРАТИЧНОЙ
ФУНКЦИИ»
Выполнил:
Чернов Лев
ученик 8 Г класса
МОУ СОШ № 49
Руководитель:
Яковлева Л. Г.
учитель математики
СОДЕРЖАНИЕ
 Введение
 Основная
часть
 Заключение
 Приложение (электронный
справочник)
ЦЕЛИ И ЗАДАЧИ
Цель работы:
 Рассказать о квадратичной функции, узнать
самому о ней кое-что новое.
Задачи работы:
 Изучить теоретический материал по данной теме.
 Научиться выполнять различные преобразования
графиков квадратичной функции.

Показать применение графика функции в
разных областях.
 Составить электронный справочник по теме
«График квадратичной функции».
Квадратичная функция - функция, которую можно
задать формулой вида
, где
.
Многие свойства квадратичной функции зависят от
значения дискриминанта. Дискриминант вычисляется по
формуле
.


Появлением параболы человечество обязано
древнегреческим геометрам. Эллипс, гипербола и парабола
были получены как конические сечения. Наиболее
интересные результаты о конических сечениях получил
математик Аполлоний (III век до н.э.), живший в
малоазиатском городе Пергаме. В своём основном труде
«Конические сечения», состоящем из восьми книг он
доказал, что все три кривые можно получить, пересекая
один и тот же конус плоскостями, по-разному
наклонёнными к оси конуса. Идеи Аполлона Пергского
оказали большое влияние на развитие
естествознания нового времени.
Если провести сначала сечение кругового конуса,
перпендикулярное
его оси, а потом поворачивать
секущую плоскость, оставляя одну точку её пересечения с
конусом неподвижной, то увидим как окружность будет
сначала вытягиваться – получится эллипс, потом вторая
вершина эллипса уйдёт в бесконечность и вместо
эллипса получится парабола, а потом плоскость
пересечёт и вторую полость конуса и получится
гипербола. Значит, парабола в некотором смысле слова
является кривой, промежуточной между эллипсом и
гиперболой.
ВИДЫ ПРЕОБРАЗОВАНИЙ
 преобразование симметрии относительно оси ox
f (x) ―> - f (x);
 преобразование симметрии относительно оси
oy f (x) ―> f (-x);
 параллельный перенос вдоль оси ox f (x) ―> f (x-l);
 параллельный перенос вдоль оси oy f (x) ―> f (x)+m;
 сжатие и растяжение вдоль оси ox, oy f (x) ―> k f (x),
k > 1, растяжение
0 < k < 1, сжатие;
ПРЕОБРАЗОВАНИЕ
СИММЕТРИИ
ОТНОСИТЕЛЬНО ОСИ OX
F (X)
―> -
F (X)
y=x2
y=-x2
ПРЕОБРАЗОВАНИЕ
СИММЕТРИИ
ОТНОСИТЕЛЬНО ОСИ OY
F (X)
y=(- x)2
―> F (-X)
y= x2
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС ВДОЛЬ
F (X) ―> F (X)+M
y= x2
y= x 2-6
ОСИ OY
СЖАТИЕ И
РАСТЯЖЕНИЕ ВДОЛЬ ОСИ OY
F (X)
―> K
F (X)
y= 2x²
y=x²
СЖАТИЕ И
РАСТЯЖЕНИЕ ВДОЛЬ ОСИ OY
F (X)
―> K
F (X)
y=x²
y=1/2x²
АЛГОРИТМ 1. (ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
Y
= F(X+L) + M )
1. Построить график функции у = f(x).
2. Осуществить параллельный перенос графика у = f(x) вдоль
оси х на |l| единиц масштаба влево, если l>0, и вправо, если
l<0.
3. Осуществить параллельный перенос полученного на
втором шаге графика вдоль оси у на |m| единиц масштаба
вверх, если m>0, и вниз, если m<0.
АЛГОРИТМ 2. (ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ
Y = F(X+L) + M )
1. Перейти к вспомогательной системе координат, проведя
(пунктиром) вспомогательные прямые x = - l и y = m, т.е.
выбрав в качестве начала новой системы координат точку (
-l; m ).
2. К новой системе координат привязать график функции у =
f(x).
КОМБИНАЦИИ
РАЗЛИЧНЫХ
ПРЕОБРАЗОВАНИЙ ФУНКЦИЙ
y= х2
y=2 (x-6)2 - 4
ПАРАБОЛЫ В ФИЗИЧЕСКОМ
ПРОСТРАНСТВЕ.


Траектории некоторых космических тел (комет, астероидов других),
проходящих вблизи звезды или другого массивного объекта (звезды
или планеты) на достаточно большой скорости имеют форму параболы
(или гиперболы). Эти тела вследствие своей большой скорости не
захватываются гравитационным полем звезды и продолжают
свободный полёт. Это явление используется для гравитационных
манёвров космических кораблей (в частности аппаратов Вояджер).
При отсутствии сопротивления воздуха траектория полёта тела в
приближении однородного гравиационного поля представляет собой
параболу.
Параболический компас
Леонардо да Винчи

Также параболические зеркала используются в
любительских переносных телескопах систем
Кассергена, Шмидта - Кассергена, Ньютона, а в
фокусе параболы устанавливают вспомогательные
зеркала, подающие изображение на окуляр.


Форма параболы иногда используется в архитектуре для
строительства крыш и куполов.
При вращении сосуда с жидкостью вокруг вертикальной оси
поверхность жидкости в сосуде и вертикальная плоскость
пересекаются по параболе.
ЛИТЕРАТУРА: