Презентация - Математико-механический факультет СПбГУ
реклама

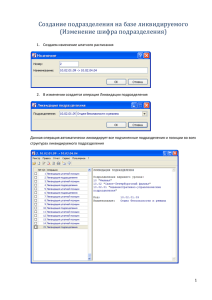
Кафедра
параллельных алгоритмов
Математико-Механический факультет
Санкт-Петербургский Государственный Университет
Параллельные алгоритмы
для симплициального подразделения области
с итерационным измельчением вблизи
границы
Дипломная работа студента 543 группы
Хрусталева Дмитрия Максимовича
Научный руководитель: д. ф.-м. н., проф. Юрий Казимирович Демьянович
Введение
Основные концепции:
Симплициальное подразделение области
Применения:
Решение
задач аппроксимации
Рис.1:Триангуляция области.
Вейвлетная обработка сигналов
Численное решение задач математической физики
Аппроксимация функции на области
Курантовская аппроксимация функции
Уточнение аппроксимации функции
на границе области
Измельчение симплициального
подразделения области
при приближении к границе
Рис. 2:Неравномерное разбиение.
Постановка задачи
Создание параллельной версии алгоритмов измельчения
симплициального подразделения при приближении к одному из
оснований заданного прямоугольного параллелепипеда.
Построение модели курантовской аппроксимации функции на
полученном симплициальном подразделении.
Разработка пакета программ, реализующих предложенные
алгоритмы для реальных вычислительных систем.
Формализация условий
• Входные данные:
• параллелепипед
П = { (x,y,z) | -S<x<S, 0<y<y*, 0<z<z* }
S,y*,z* - положительные числа
• Задача алгоритма:
• построение симплициального подразделения параллелепипеда П с
измельчением вдоль оси z;
• полученное разбиение должно быть топологически правильным
• среди симплексов подразделения не должно оказаться
вырожденных
Последовательная версия алгоритма
- “Алгоритмы невырожденного симплициального
подразделения с измельчением вблизи границы”,
Е.П. Арсентьева, Ю.К. Демьянович.
- Основная идея: разделить параллелепипед на
горизонтальные полосы, и строить отдельное
симплициальное подразделение для полос по очереди.
- Полученный симплициальный комплекс бесконечен;
критерий остановки алгоритма – достижение требуемой
точности
Последовательная версия алгоритма:
Симплициальное подразделение полосы
Рис. 3:Алгоритм симплициального подразделения полосы.
Последовательная версия алгоритма:
Симплициальное подразделение полосы
Рис. 4:Симплициальное подразделение вертикальной треугольной призмы.
Распараллеливание алгоритма
Рис. 5:Схемы разбиений последовательных горизонтальных слоев.
• Количество треугольников растет
экспоненциально
• Для вычислений, связанных с
вершиной, требуются данные
только о соседних вершинах
• Разбив слой на области, можно
выполнять расчеты независимо
Рис. 6:Разбиение текущего слоя на области.
Реализация
Позволяет задавать алгоритмы
Выбора точки при разбиении ребра
Оценки достигнутой точности аппроксимации
Разбиения текущего слоя на области
Не зависит от платформы
Может использоваться как отдельное
приложение и как библиотека
Полученные данные
Рис. 7:Перспективные проекции полученной адаптивной сетки.
Число шагов
1 поток
2 потока
3 потока
4 потока
5
0
0
1
1
6
16
12
11
11
7
78
41
30
22
8
281
145
101
76
9
1125
568
390
301
10
4609
2324
1578
1189
11
18844
9510
6342
4782
Таблица: время работы программы в различных условиях.
Результаты
В данной работе создан параллельный алгоритм,
выполняющий построение симплициального
подразделения области с итерационным измельчением
вблизи границы.
Результатом работы полученного алгоритма является
топологически правильное симплициальное
подразделение заданного прямоугольного
параллелепипеда, измельчающееся при приближении к
его нижнему основанию.
Разработан программный пакет, реализующий
предложенный алгоритм
Предложены направления для дальнейшего улучшения
полученного алгоритма.