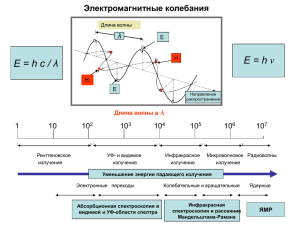
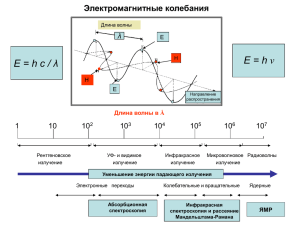
L_2_1

Излучение и поглощение. Коэффициенты Эйнштейна
Разложение поля в ряд по бегущим плоским волнам
k  ω/ c
- волновое число
E   A, H  rotA
A(r , t )   ekρ (akρ e
k
ekρ
ikr
a e
*
kρ
ρ
 ikr
)
akρ ~ e  iωt
- единичный вектор поляризации
Переход к каноническим переменным




1
iω
*
*
Qkρ 
akρ  akρ ; Pkρ  
akρ  akρ  Qkρ
4π
4π
Обобщенная координата
Обобщенный импульс
Излучение и поглощение. Коэффициенты Эйнштейна
Функция Гамильтона
1
H   (Pkρ +ω2Qkρ )
2 kρ
Каждый член суммы соответствует бегущей волне с заданными значениями
волнового вектора и поляризации и имеет вид, аналогичный виду для
одномерного гармонического осциллятора.
Поэтому полученное разложение поля в ряд называется разложением поля
на осцилляторы
Правила коммутации канонических операторов:
Pˆkρ Qˆ k 'ρ'  Qˆ k 'ρ' Pˆkρ  i, k  k ', ρ=ρ'
Pˆkρ Qˆ k 'ρ'  Qˆ k 'ρ' Pˆkρ  0, k  k ' или ρ  ρ'
Гамильтониан поля:
Ê 


1
ˆ2 ˆ 2
E
 H dr

8π
ˆ  1  (Pˆ 2  ω2Qˆ 2 )
H
kρ
2 kρ kρ
Излучение и поглощение. Коэффициенты Эйнштейна
Cобственные значения гамильтониана соответствуют собственным
значениям гамильтониана одномерного гармонического осциллятора и
определяют уровни энергии поля:
1
E   ω(Nkρ + )
2
kρ
N kρ
- целые числа, определяющие число осцилляторов поля с данным
значением энергии
Классическое выражение для импульса поля:
Тогда:
1
P
[ EH ]dr

4π
1

ˆ 1
2
2 k
ˆ
ˆ
P   ( Pkρ  Qkρ ) ; P   k  N kρ  
2 kρ
ω
2

kρ
Выражения для энергии и импульса определяют энергию и импульс частиц,
движущихся со скоростью света и имеющих нулевую массу покоя. Тогда
N kρ
- число частиц – фотонов – имеющих заданные значения волнового
числа и поляризации
Излучение и поглощение. Коэффициенты Эйнштейна

1
cˆkρ 
ωQˆ kρ  iPˆkρ
2ω


1
+
+
ˆ
ˆ
ˆ
ˆ
H   ω ckρ ckρ  ckρ cˆkρ
2 kρ




ˆ
A   cˆkρ Akρ  cˆk+ρ Ak*ρ ;
kρ

1
cˆ 
ωQˆ kρ  iPˆkρ
2ω
+
kρ
Akρ 

2π
ekρ eikr
ω
ˆ
E   cˆkρ Ekρ  cˆk+ρ Ek*ρ ; Ekρ  iωAkρ
kρ
k

ˆ
+
*
H   cˆkρ H kρ  cˆkρ H kρ ; H kρ   , Ekρ 
kρ
ω




Излучение и поглощение. Коэффициенты Эйнштейна
 N kρ  1 ck+ρ N kρ    N kρ ckρ N kρ  1   ( N kρ  1)
ck+ρ
соответствует появлению в поле нового фотона (испусканию или
излучению фотона) и поэтому называется оператором рождения фотона
ck+ρ
соответствует поглощению фотонаи поэтому называется оператором
рождения фотона
Nkρ  0 :  1 ck+ρ 0    0 ckρ 1   1
Процесс излучения фотона может произойти даже при отсутствии фотонов
в начальном состоянии поля
Процессы излучения и поглощения делятся на три категории – спонтанное
и вынужденное излучение, вынужденное поглощение
 N kρ  1 ck+ρ N kρ    N kρ ckρ N kρ  1 
спонтанное излучение
вынужденное излучение
вынужденное поглощение
Излучение и поглощение. Коэффициенты Эйнштейна
Ea
Вероятность переходов между состояниями
a
dWab 
wab
Eb
b
2π
Vab δ( Ea  Eb  ω)dν
2
Vab - матричный элемент возмущения, приводящего
к переходу из состояния b в состояние a
ν  ω  Ea  Eb  ω  Wab 
2π
Vab
2
Гамильтониан атома, находящегося в электромагнитном поле:

ˆp 2  e Aˆ
c
ˆ
H
2m
  pˆ
2
ˆ
e2 A2
e ˆ ˆ ˆ ˆ
ˆ  Hˆ '


pA

Ap

H
0
2
2m 2mc 2mc
2


Излучение и поглощение. Коэффициенты Эйнштейна

e ˆˆ ˆˆ
ˆ
ˆ
V  H'
pA  Ap
2mc
Тогда:


e ˆ
ˆ
H'
pekρ aˆkρ eikr  aˆk*ρ e  ikr
mc

Отличные от нуля матричные элементы этого оператора:
e
 N kρ  1 H ' N kρ   
mc
e
 N kρ  1 H ' N kρ   
mc
2 c 2 ( N kρ  1)
ω2
2 c 2 N kρ
ω2
ekρ  b peikr a 
ekρ  a peikr b 
Излучение и поглощение. Коэффициенты Эйнштейна
При переходе системы в состояние с большей энергией количество
фотонов в поле уменьшается на единицу (вынужденное поглощение фотона)
При переходе системы в состояние с меньшей энергией происходит
испускание фотона (спонатнное и вынужденное излучение)
dWab 
2
2
H 'aNkρ ,bNkρ 1 δ( Ea  Eb  ω)dω
Отношения вероятностей излучения и поглощения:
- для дифференциальных величин
- для интегральных величин
N kρ  1
dWab dWизл


dWba dWпогл
N kρ
N kρ  1
Wизл

Wпогл
N kρ
Излучение и поглощение. Коэффициенты Эйнштейна
Соотношение между интенсивностью поля, взаимодействующего с системой,
и количеством фотонов в этом поле
Число фотонов в единице объема
2π
ki 
ni
L
3
V
 L 
2
n  nx n y nz    k ; dn 
dk

k
dkd 
3
(2π)
 2π 
I kρ dωd
- энергия излучения поля, которое падает на единицу
площади поверхности, имеет частоту в интервале dw,
определенную поляризацию, и волновой вектор в
телесном угле d
k 2 dkd
В этом диапазоне количество осцилляторов равно:
(2π)3
На каждый осциллятор приходится
N kρ
фотонов
Излучение и поглощение. Коэффициенты Эйнштейна
k 2 dkd 
ω3
8π3c 2
Тогда c
N kρ ω  3 3 N kρ dωd ; N kρ 
I kρ
3
3
(2π)
8π c
ω
После этого получаем:
инд
dWkпогл

dW
ρ
kρ
3 2
8π
c
сп
 dWkρ 
I kρ
3
ω
В случае, если поле не поляризовано и изотропно, полученное выражение
можно проинтегрировать:
W погл  W инд
2 2
8π
c
сп
W 
I ; I  8πI kρ
3
ω
Коэффициенты Эйнштейна для спонтанного излучения, вынужденного
излучения и вынужденного поглощения
A W ; B
сп
изл
W
изл
c
погл
погл c
; B
W
I
I