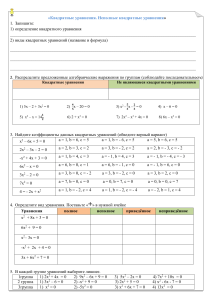
Формулы корней квадратного уравнения
реклама

Формулы корней квадратного уравнения axbx c0 2 2 ax bx c0 b a (x x ) c 0 a 2 2 2 b b b a ( x 2 x ) c 0 2 2 2 a4 a4 a 2 2 2 b b b a ( x 2 x 2 ) c 0 2 a4 a4 a 2 2 b2 b 4 ac a ( x ) 0 2 a 4 a 2 b2 b 4 ac a ( x ) 2 a 4 a b2 4 ac D b2 D a (x ) 2 a 4 a Обозначим : b x y, 2a D 2 y 2 4a D D y 2 4 a 2 a b D (x )2 2 2 a 4 a b D x 2a 2a b D x 2a 2a b D x 2a Итак, чтобы найти корни квадратного уравнения, надо: 1.Вычислить дискриминант квадратного уравнения. Если дискриминант-число положительное, то уравнение имеет два различных корня. Если дискриминант равен нулю, то уравнение имеет один корень. Если дискриминант-число отрицательное, то уравнение не имеет корней. Db2 4ac 2.Вычислить корни квадратного уравнения по формуле: b D x 2a Решить уравнения: №1. 7x29x20 a7 ,b9 ,c2 2 D 9 4 7 2 81 56 25 0 9 25 x 27 95 x 14 95 x 1 1 14 9 5 4 2 x 2 14 147 2 x 1 , x 1 2 7 №2. 6x2x10 a6 ,b 1 ,c 1 2 D 1 4 6 ( 1 ) 1 24 25 0 1 25 x 26 1 5 x 0 ,5 1 12 15 1 x2 12 3 1 Ответ : 0 ,5 ; . 3 №3. x27x80 a 1 ,b 7 ,c 8 2 D ( 7 ) 4 1 ( 8 ) 49 32 81 0 ( 7 ) 81 7 9 x 2 1 2 79 x1 8 2 79 x2 1 2 Ответ :1;8 №4. 3x2 60 a 3 ,b 0 ,c 6 2 D 0 4 ( 3 ) 6 0 72 72 0 0 72 x 2(3) 72 36 2 x 6 6 6 2 x 2 1 6 62 x 2 2 6 Ответ :2 , 2 . Или : 3x2 60 3x2 60 3x 2 6 x2 2 x 2.