Capillary wave turbulence at the charged surface of liquid hydrogen

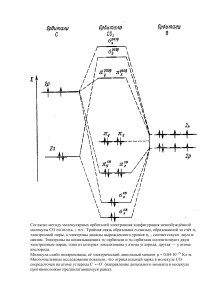
Capillary wave turbulence
at the charged surface of liquid hydrogen
G.V. Kolmakov
ISSP RAS & Lancaster University
M.Yu. Brazhnikov,
A.A. Levchenko,
L.P. Mezhov-Deglin,
Institute of Solid State Physics
RAS, Russia
A.N. Silchenko,
P.V.E. McClintock
Lancaster University, UK
Short content
• Introduction
Liquid hydrogen as a test fluid for studies of nonlinear
wave phenomena.
• Linear and nonlinear waves at the charged surface of
liquid hydrogen. Steady state turbulence of capillary
waves.
• Relaxation of the turbulent cascade after switching off
the outer driving force.
• Suppression of turbulence by an additional lowfrequency driving.
• Conclusions.
Properties of liquid hydrogen, helium and water
Liquid Hydrogen,
T=15 K
Liquid Helium,
T=4.2 K
Water,
T=300 K
0.076
0.145
1.0
Surface tension ,
dyn/cm
2.7
0.12
77
Capillary length ,
cm
1.18
0.18
1.74
Nonlinearity
coefficient (/3)1/4,
cm9/4/g1/2s1/2
8.9
2.5
3.0
Kinematical viscosity
, cm2s
0.0026
0.00002
0.01
Dielectric permittivity
1.26
1.047
81
Density , g/cm3
e
Usage of liquid hydrogen as a test liquid
for studies of capillary turbulence
• High nonlinearity coefficient, low viscosity: The inertial range of
frequencies is an order wider in “conventional fluids” (water).
• Possibility to create quasi-2D charged layer below the liquid surface.
The dispersion management by application of external electric field.
• Small density, excitation of surface oscillations by weak oscillating
electrical field. Driving force acts directly on the surface.
• Very pure conditions of excitations (e.g., with respect to the vibrating
platform techniques).
• Spectral characteristic and angle dependence of the driving force
can be varied in a controllable way in vide limits.
Experiments with the charged surface of liquid hydrogen
K.R. Atkins, Phys. Rev. 116, 1339 (1959)
Pe = p0 e2 / (2 vH r4);
R4+ = p0 e2 / (2 vH Ps)
p0 – polarizability, 1·10-24 см3
vH – effective volume  4.4 10-23 см3
Estimated R+ ≈ 45 Å.
Experimental R+ ≈ 15 Å
Positive
charge
U
d
E
LIQUID HYDROGEN
Radioactive plate (source of charges)
Negative charge
R.A. Ferrel, Phys. Rev. 108, 167 (1937)
W=(h2/2mR2) + 4R2 + 4R3 P /3
m – mass of electron
 - surface tension.
At zero pressure
R4 = ( h2 / 8m).
R- 10Å.
Linear waves on the neutral surface of liquid
Dispersion law for linear capillary-gravity waves (waves of small amplitude)
In accordance with the previous table,
for water at T=20 C one has: kc=3.6 cm-1,
for liquid hydrogen at T=15 K one has: kc=5.32 cm-1.
g is the free fall acceleration
 is the surface tension
 Is the density of liquid
In case of long (gravity) waves, k<kc, the dispersion relation reads
For short (gravity) waves, k>kc, the dispersion relation is the following
Linear waves on the charged surface of liquid hydrogen
What is the influence of charges localised below the surface?
Here we consider the case where the quasi-two dimensional charged layer screens
totally the external electric field (E≠0 in gas phase, only)
– that corresponds to condition of experiments with the positively charged surface of
liquid hydrogen.
The sigh of charges localised below the surface is defined by
polarity of the voltage U applied between the surface and the
upper electrode.
U
d
E
r
Three types of charges in liquid H2:
Negative charges – electron bubbles (cannot be stabilised
below the surface due to relatively high probability of quantum
tunnelling through the surface); and negatively charged clusters
(snowballs) H2– complexes surrounded by a solidified layer of
hydrogen.
Positive charges – positively charged clusters (used in our
experiments with nonlinear capillary waves).
(Mezhov-Deglin and Levchenko, 1997)
In experiments with charged surface the two-dimensional density of positive charges
stabilised below the surface is equal to
n~1010 charges/cm2
Mean distance between charged clusters in the 2D layer is equal to
r ~ n-1/2 ~10-5 cm
So, in case of waves with the wave length >r~10-5 cm we may consider the
distribution of charges quasi-continuously.
The dispersion law for capillary waves at the charged surface of liquid in “quasicontinuous” approximation has been calculated by D. Chernikova in 1976.
U
d
E
It is of importance that in the case of waves on the charged surface of liquid
there is an additional parameter with the dimensionality of length –
the distance d between the charged surface and the upper flat electrode.
And this distance should be compared with the capillary wavelength c.
(Note that we consider the waves on the surface of deep layer of liquid, <<h,
where h is the depth of liquid, so th(kh)1.)
1. Large d (d>> c)
Evolution of the spectrum of waves on the
charged surface of liquid with increasing the
voltage U (the case of large d).
This type of spectrum has been studies by P. Leidered
in 1979, in experiments with positively charged
interface in a phase-separated 4He-3He mixture.
In this case the dispersion relation reads:
The term in the dispersion relation, which appears due to electrical forces, is underlined.
The dispersion relation:
At high electric fields
a flat surface becomes unstable.
Spectrum of waves on the flat charged
surface of liquid at high electric field E>Ec .
The instability (in case of fixed total number of charges) leads to formation of
multi-charged dimples with characteristic sizes ~ kc-1, or to formation of dimple
crystal, in dependence of total number of charges – the reconstruction of the
surface takes place.
Dimple crystal formed on the free surface
of superfluid helium at high electric fields (Leiderer, 1979).
2. Small d (d<< c)
In the case where the distance d is relatively small, d<a the dispersion law
acquires the following simple form
E<Ec
where the effective free fall acceleration is give be
the following equation
So, electrical field renormalizes the free fall acceleration g:
E>Ec
Unstable region.
The effective free fall acceleration is decreased with increasing the electric field.
At G<0 a flat surface becomes unstable, but the instability is developed
at small k << kc, first (long-wave instability).
Reconstruction of the charged surface
of liquid hydrogen at high electric fields
At U>Uc the surface is reconstructed and a stationary, solitary-like wave
of the surface deformation is formed, where
Z, mm
Solitary wave of deformation formed on
the charged surface of liquid hydrogen at
U>Uc
r, mm
Dependence of the maximal angle of
reflection of a laser beam from the surface
and of its derivative on the voltage applied.
A.A. Levchenko et al, 1997.
At high voltages, U>Uc2, the geyser-like discharge of the surface take place.
U, V
Snapshot of the surface at the moment of the geyser formation.
T, K
Phase diagram of soliton stability at the charged surface of liquid hydrogen.
The first critical voltage is equal to
Intensity
Spectrum of linear oscillations
of the charged liquid hydrogen surface
Scheme of measurements
Log w (Hz)
Measured intensity of the laser beam
measured by a photodetector.
At G0 the surface waves have a purely
capillary dispersion law for all wave length.
Log k (cm-1)
The dispersion curve for the waves on the
charged surface of liquid hydrogen. The
depth of the liquid layer was 2.7 mm. The DC
voltage was U = 283 V (circles), 954 V
(squares), and 1080 (diamonds).
So, we can manage the dispersion
of waves by changing the applied
voltage U
Nonlinear capillary waves
on the surface of liquid hydrogen
Multiple frequency generation
and cascade-like transfer of
energy to high frequency due to
nonlinearity
INERTIAL
RANGE
Log Ew
Ew~w-3/2
Log w
Energy flux P >0
DAMPING
PUMPING
The dispersion relation for capillary
waves is of decay type w ~ k3/2
k=k1+k2
w=w1+w2
(E is the only integral of motion, no inverse cascade)
For capillary wave turbulence (V.E. Zakharov, A.N. Filonenko, 1967):
In the inertial range:
Ew~w-3/2
The theory of weak turbulence presents a basis for description of dynamics of
capillary waves. (Zakharov, Filonenko, 1967)
The amplitude of three-wave interaction for capillary waves
The kinetic equation for capillary waves
where
-- “number of waves” with the wave vector k.
ak(t) – normalised (canonical) amplitude of the wave.
-- the damping coefficient for capillary waves.
Steady-state spectrum of capillary turbulence (Zakharov, Filonenko, 1967).
Where kp is the characteristic scale of pumping,
kb is the viscous scale (short-wave edge of the inertial range).
Previous studies of capillary turbulence on the surface of water
E. Henry, P. Alstrom and M.T. Levinsen,
Europhys. Lett, 52, 27 (2000).
The observed spectra of capillary
waves on the liquid surface
(experiments with water in a cell
placed on a vibrating platform).
1.W. Wright, R. Hiller and S. Putterman, J.Acoust.
Soc. Am., 92, 2360 (1992).
Power of the reflected
laser beam, a.u.
Experimental studies of turbulence of capillary waves
on the surface of liquid hydrogen (Levchenko at al, 1999)
Scheme of registration of the surface oscillations
Iw = <|w|2> = <|w/k|2> =
= k2<|w|2>~w4/3<|w|2>,
where w= kw - angle amplitude of the
wave.
w2~ Pw2/ Ф(w)
Thin beam (ka<<, where a – is the laser spot size)
Ф(w)1
Iw ~ w4/3 <|w|2> ~ w4/3 Pw2
Broad beam (ka>>) Ф(w) ~ w4/3
Iw ~ w4/3 <|w|2> ~ Pw2
Time, s
Time dependence of the registered signal
P(t);
the driving frequency is equal to
w/2 = 27.5 Hz.
Apparatus function Ф(w) = Pw2/ w2
Spectrum of oscillation of liquid hydrogen surface
Driving at a single frequency
6
10
5
10
4
10
3
10
2
10
m= -3.7
P
2
w
1
10
0
10
10
-1
10
-2
10
-3
10
-4
10
1
2
10
3
10
4
10
Frequency, Hz
Spectrum of surface oscillations
measured in case where the driving
frequency is equal to 28 Hz
Spectrum of surface oscillation; driving
frequency is equal to135 Hz
In the frequency range up to 10 kHz the spectrum of oscillations
can be approximated as follows
Iw ~ Pw2= const w -21/6
Excitation
at 28 and
48 Hz
Excitation by
a noisy force
Pw2=const w -17/6
In agreement with the results
of the weak turbulence theory
(by Zakharov, Shafarenko,
1967)
Modification of the spectrum of oscillations with changing
the spectral characteristics of the driving force.
nk~k-21/4
(Iw ~ w-21/6)
Spectral density of the surface
elevation shown (noisy driving force;
numerical calculations by
V.E. Zakharov,
A.N. Pushkarev, 1996)
nk~k-17/4
Stationary distribution nk for
capillary waves calculated for
the case
of spectrally sharp driving
(G.E. Falkovich, A.B.
Shafarenko, 1988)
(Iw ~ w-17/6)
High frequency cut-off of the power spectrum of turbulence
Characteristic time of the nonlinear
interaction of waves
1/n(w)~|Vkkk|2 n(k) k2 / wk ~ A02w-1/6
Time of viscous (linear) dumping.
1/v (w) ~2 k2 ~ w4/3
n~v
Distribution of Pw2 measured in the case where
the amplitude of wave at the driving frequency
135 Hz is equal to 0.016 mm. Arrow marks the
high-frequency boundary of the inertial range.
12
4/3
Frequncy wb/2, kHz
10
wb=0.45+5800
Coefficient of nonlinear interaction
Vkkk~(/3)1/4 k 9/4
4/3
wb=0.35+743
8
Spectrum of waves
6
n(k) = const A02 (k/kp) -21/4
4
The dispersion law
2
0
0.00
w(k) ~ k3/2
4/3
wb=0.27+196
0.01
0.02
0.03
Amplitude , mm
0.04
0.05
Dependence of high-frequency boundary of the inertial
range on the amplitude of the wave at driving frequency.
The driving frequency is 83 Hz (lower curve), 135 Hz
(middle curve), and 290 Hz (upper curve).
If one supposes that
One has
wb~ A04/3wp23/9
An important conclusion is followed from this result:
Despite our system has a finite sizes (L is of a few cm order), and,
consequently, the intrinsic spectrum of small oscillations of the surface
is discrete, the position of the high frequency edge of inertial range is
controlled by viscosity, not by discrete character of the spectrum.
Non-stationary processes of turbulence decay
The recorded signal P(t) after the
removal of the driving force (the driving
frequency is 98 Hz).
Evolution of spectrum of the surface
oscillations after the removal of the driving
force.
What we are waiting for?
An initial assumption – the self-similar process of formation and decay
Formation
The self-similar variable
The self-similar function
The front position
Such scenario of the decay of capillary turbulence is in
contradiction with the observations.
Decay
P(t), arb. units
Non-stationary processes of turbulence decay
, s
Time, s
Relaxation of the surface oscillations after
removal of the driving. Upper plot: small cell,
wp=98 Hz, Lower plot: large cell, wp=97 Hz.
 ~ w -4/3
wp /2 , Hz
Dependence on time of the amplitude of the
recorded signal P(t): curve 1 for a driving frequency
w p= 97 Hz; and curve 2 for w p= 173 Hz (large cell).
Dependence of the effective relaxation time  of the
surface oscillations on the driving frequency wp (circles);
and viscous damping time for capillary wave gw-1 with
frequency wp, calculated from known parameters of liquid
hydrogen (line).
A.A. Levchenko, M.Yu. Brazhniov, L.P.Mezhov-Deglin, G.
V. Kolmakov, A.N. Silchenko, P.V.E. McClintock, JETP
Lett. 80 (2) 99-103 (2004); Phys. Rev. Lett. (2004).
Decay of the capillary turbulence on the surface of viscous liquid.
The main conclusion: the dissipation is missed in the previous consideration.
t=0 – the moment when the pumping is removed
kb(t) – the position of the edge of the inertial range
at the moment of time t,
 – some exponent,
g() – self-similar function,
 – self-similar variable
The main assumption: the evolution is controlled
by the position of the inertial interval edge.
Equation for the self-similar function
where
The position of the inertial range edge kb(t) is governed by the following equation
where
The viscosity coefficient and the C constant can be excluded from the equation by
using the following substitution:
The boundary conditions are:
1)
2)
Asymptotes of the self-similar function:
(Energy distribution over frequency
)
“Local” approximation in the theory of capillary turbulence
Steady-state distribution
1
0.01
0.0001
In this simple model the self-similar representation
for the spectrum of capillary waves during the free
decay s the following
1.
10
6
1
2
5
10
20
Steady-state spectrum of
turbulence in the local model.
- Is the self-similar variable in scales of frequency
Equation for the self-similar function is the following
The results of numerical integration of the equation (1) for
f(x) in cases f(1) = f1 = 100,10, 1 и 0.1, plotted in
logarithmic scales. Dashed lines corresponds to
asymptotes x-2/3 и x-3/2.
Numerical studies of the decay of capillary turbulence
Evolution with time of the energy distribution of capillary waves Ew after step-like
switching off the driving force:
1: t = 0 (steady-state spectrum), 2: t = 0.5, 3: t = 2.0 и 4: t = 4.0.
Dashed line corresponds to the power spectrum Ew ~ w-3/2.
Time and frequency is shown in dimensionless units.
Position of the high-frequency edge of the inertial frequency wb(t) obtained in
numerical calculations (squares); and the
Plotted for wb(0) = 32.7 and  = 0.187 (solid curve).
In experiments on the decay of capillary turbulence on the surface of iquid
hydrogen the relative width of the inertial range is
wb/wp ~ 50 - 100
Characteristic time of nonlinear interaction of waves with the frequency w
Time of viscous damping
In case of pumping by a low-frequency noise
At the frequencies of the order of the boundary frequency of the inertial
range
At the pumping frequency
Suppression of turbulence at high frequencies by low frequency driving
Pumping at w1/2 = 61 Hz и w2/2 = 274 Hz.
Squared amplitudes of waves at the pumping
frequencies w1/2 = 61 Hz и w2/2 = 274 Hz. The
low-frequency driving is removed at t = 0.
а
б
Squared amplitudes of waves at the multiple
frequencies of w2/2 = 274 Гц.
Stationary spectra of surface oscillations before
and after switching off the low frequency
perturbation.
Pumping at w1/2 = 63 Hz and w2/2 = 178 Hz.
а
б
Stationary spectra of capillary turbulence. Red  pumping at
two frequencies w1/2 = 63 Hz and w2/2 = 178 Hz, blue 
pumping at w2only.
Squared amplitudes of waves at the multiple frequencies of the main pumping frequency at
switching on (а) and at switching off (б) the additional low-frequency driving.
The “classical” wave
turbulence view.
The energy flux to high
frequencies
So, the energy flux should increase
when the driving frequencies is
decreased
Подавление высокочастотных турбулентных колебаний
Calculated evolution of the spectra after
switching off the additional low-frequency
driving.
The inset: the relative changes of the peak
amplitudes
The reason of the suppression of turbulence at high frequencies is
the change of density of states involved in the nonlinear transfer of
energy to high frequencies.
Подавление высокочастотных турбулентных колебаний
Впервые изучена динамика установления стационарного
турбулентного каскада в системе капиллярных волн на поверхности
жидкого водорода при включении/выключении дополнительной накачки с
частотой ниже частоты основной накачки.
Обнаружено, что при включении дополнительной низкочастотной
накачки амплитуды волн в высокочастотной части турбулентного спектра
уменьшаются, что приводит к сокращению инерционного интервала
частот.
При выключении низкочастотной составляющей накачки
амплитуды высокочастотных турбулентных осцилляций увеличиваются,
инерционный интервал расширяется.
Экспериментальные данные и результаты проведённых нами
численных расчётов качественно согласуются между собой.
Выводы
Таким образом, в работе изучен распад капиллярной
турбулентности на поверхности жидкости после ступенчатого
выключения внешней возбуждающей силы с учетом вязкого
затухания волн на всех частотах. Из результата расчета следует,
что распад турбулентности начинается с области высоких частот.
При достаточно больших начальных амплитудах возбуждающей
силы распределение энергии волн по частотам близко к своему
стационарному виду Ew ~ w-3/2 в широком интервале частот w <
wb, где wb - граничная частота инерционного интервала, в течение
относительно длительного времени после выключения внешней
силы. После выключения внешней силы граничная частота wb
уменьшается, и при больших временах t >> , где t -характерное время распада турбулентности, wb(t) ~ t-3/4.
Полученные результаты качественно согласуются с результатами
экспериментов по изучению распада капиллярной
турбулентности на поверхности жидкого водорода.
CONCLUSIONS
•
Liquid hydrogen is an excellent test fluid for studies of general static and
dynamic nonlinear phenomena, and for careful check of predictions of WT
theory.
•
At high electric fields a steady solitary-like wave of the surface deformation is
formed at the charged surface of liquid hydrogen. Reconstruction of the
surface has a soft character and close to the second-order phase transition.
•
The remarkable properties of liquid hydrogen have allowed us to observe and
study turbulence of capillary waves
a) the power-like spectrum of capillary turbulence in a wide range of
frequencies up to 10 kHz;
b) The cut-off the power spectrum is observed at high frequencies caused
by change of the mechanism of the energy transfer from the nonlinear waves
transformation to viscous damping.
•
Free decay of the turbulence has a quasi-adiabatic character. The fast
redistribution of energy between waves inside the inertial range damps a
propagation of the front through the scales. The turbulent system is in quasisteady state during the decay. The high frequency edge of the inertial range
goes to low frequency. Account for the finite viscous losses at all frequencies
changes qualitatively the character of the decay of turbulence.
List of Recent Publications
1. A.A. Levchenko, M.Yu. Brazhniov, L.P.Mezhov-Deglin, G. V. Kolmakov, A.N.
Silchenko, P.V.E. McClintock,
“Decay of the turbulent cascade of capillary waves on the charged surface of liquid
hydrogen”, JETP Lett. 80 (2) 99-103 (2004);
2. G. V. Kolmakov, A.A. Levchenko, M.Yu. Brazhniov, L.P.Mezhov-Deglin, A.N.
Silchenko, P.V.E. McClintock,
“Quasi-adiabatic decay of capillary turbulence on the charged surface of liquid
hydrogen”, Phys. Rev. Lett. 93 (7), 074501 (2004).
3. M.Yu. Brazhniov, A.A. Levchenko, and L.P.Mezhov-Deglin,
“Excitation and detection of nonlinear waves on a charged surface of liquid hydrogen”,
Instrum. Exp. Tech. 45 (6) 758-763 (2002).
4. M.Yu. Brazhniov, G. V. Kolmakov, A.A. Levchenko, and L.P.Mezhov-Deglin,
“Linear and nonlinear waves at the charged surface of liquid hydrogen”,
Low Temp. Phys. 27 (9-10) 876-882 (2001).
Schematic view of the relaxation process
Results of our estimations for the
decay of capillary turbulence are in
agreement with the experimental
observations
Predictions of the theory where
the dissipation was neglected
We may speak about the inverse front motion during the relaxation, but
the motion is defined by both dissipative and nonlinear processes, and it
has absolutely different meaning!
Soliton formation on the charged surface of liquid helium
(electrons above the surface of helium).
P. Leiderer, 1997
Выводы
Таким образом, в работе изучен распад капиллярной
турбулентности на поверхности жидкости после ступенчатого
выключения внешней возбуждающей силы с учетом вязкого
затухания волн на всех частотах. Из результата расчета следует,
что распад турбулентности начинается с области высоких частот.
При достаточно больших начальных амплитудах возбуждающей
силы распределение энергии волн по частотам близко к своему
стационарному виду Ew ~ w-3/2 в широком интервале частот w <
wb, где wb - граничная частота инерционного интервала, в течение
относительно длительного времени после выключения внешней
силы. После выключения внешней силы граничная частота wb
уменьшается, и при больших временах t >> , где t -характерное время распада турбулентности, wb(t) ~ t-3/4.
Полученные результаты качественно согласуются с результатами
экспериментов по изучению распада капиллярной
турбулентности на поверхности жидкого водорода.
Pw2, отн. ед.
Подавление высокочастотных турбулентных колебаний
Частота w/2, Гц
Спектрограмма колебаний поверхности жидкого водорода
при накачке на частотах w1/2 = 63 Гц и w2/2 = 178 Гц. По
оси абсцисс  время в секундах, по оси ординат 
десятичный логарифм частоты.