БИОфизика ВОДНЫХ ЭКОСИСТЕМ7 (1.7Mб, ppt)

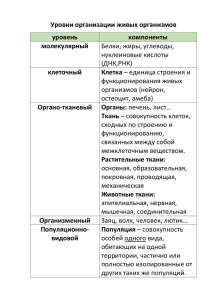
Математическое моделирование
водных экосистем
Что такое модель?
Модель - абстрактное представление
сложной «реальной» системы
Что такое модель?
Построить модель явления (смоделировать
его) – создать формальное описание
которое описывает и объясняет его
(явление)
В целом модель позволяет получить более
точное представление о моделируемом
явлении (Понимание), позволяет
анализировать его поведение и динамику
(Предсказание) и дает информацию как им
управлять (Контроль)
• Невозможно создать модель реального мира не
имея данных об этом мире.
• Сбор данных может быть «задан» модельером –
в идеале. В реальности приходиться пользоваться
тем что есть.
Детерминистские модели
 Основаны на предположениях/знаниях о
взаимосвязях между переменными в
моделируемой системе или на физических
законах и принципах.
 Более общие чем эмпирические модели.
 Нацелены на точное и полное описание
всех процессов и взаимодействий между
переменными в системе.
Динамика кислорода = диффузия + фотосинтез - потребление
разными организмами - химическое окисление
Каждая из переменных описывается как физический, химический или
биохимический процесс, зависящий от многих параметров.
Стохастические модели
Случайные события (вероятности) играют
ключевую роль.
Подходят там где случайные флуктуации в
процессах или переменных делают
детерминистские модели непригодными.
Причины случайных флуктуаций:
 Действительно случайные процессы
 Не случайные процессы знания о которых
недостаточны или неполны (кажутся случайными)
 Не систематические ошибки в измерении
параметров или переменных.
 Очень сложные процессы где случайные
стохастические методы наиболее подходят.
Эмпирические модели.
 Строятся не на основе теории или физических
законов.
 Взаимосвязь между переменными выводится из
экспериментальных данных.
 Математическое описание (функции)
взаимосвязи на основании компромисса между
точностью описания зависимости и простотой
функции (например линейная регрессия).
 Часто носят не общий характер (применимы к
конкретному диапазону значений параметров) и
соответственно не пригодны для других условий
без дополнительной калибровки.
Результаты наблюдений за поведением какой-то переменной в
зависимости от значения какого-либо параметра (например
концентрация водорослей в озере и количество фосфора в озере).
Роль модели в ответе на вопросы
Модель настолько хороша насколько хороша
определена проблема которую надо решить.
Калибровка и верификация
Выполняется для того, чтобы убедиться в
корректности результатов моделирования.
Калибровка - проверка модели в заданном
диапазоне условий и параметров.
Верификация - сравнение результатов
моделирования с независимыми
экспериментальными данными.
Анализ на чувствительность
Используется для того чтобы оценить как работает
модель в заданном (возможном) диапазоне
изменения параметров.
 Переменные — независимое варьирование переменных
с целью оценить отклик (варьирование) конечного
результата.
 Функции — оценка чувствительности результатов
моделирования к изменениям в функциях описывающих
процессы или взаимодействия в системе.
Может показать недостатки модели.
Показывает необходимый уровень точности для
каждой переменной.
Показывает области применимости модели.
Основные типы математических моделей
(применительно к водным экосистемам)
• Гидрофизические модели (динамика
водных масс, режимы
температуры/солености, ветрового
перемешивания и т.п.)
• Биологические модели (разного уровня от
популяционных до трофических цепей и
сетей)
• Динамические модели водных экосистем
(интегрирование биологических и
гидрофизических моделей в модель водной
экосистемы)
Базовые принципы построения достаточно
правдоподобной модели экосистемы:
 должна быть предусмотрена возможность учета и
использования результатов различных естественнонаучных
исследований
 должен быть предусмотрен вероятностный характер
многих параметров
 модель должна быть обеспечена математическим
аппаратом, дающим возможность исследовать задачи,
представляющие практический интерес
 добавление новой информации об экосистеме должно
легко учитываться в рамках уже построенной модели
 модель должна быть построена по модульному принципу,
причем каждый модуль верифицируется до его включения в
общую модель.
All models are wrong - but some are
useful.
Все модели неверны – но некоторые
полезны.
C. Chatfield
Blind face in what the model predicts is
not the main purpose of the modeling.
Слепая вера в то, что предсказывает
модель это не главная цель
моделирования.
W.Grimm
У каждой модели должны быть границы:
Временные
…
Пространственные
Клетка
Иерархические
Организм
Популяция
Экосистема??
Моделирование популяционной
динамики гидробионтов.
• Беляева Н.Е., Ризниченко Г.Ю., Рубин А.Б.
Динамические модели в биологии.
Электронный ресурс:
http://dmb.biophys.msu.ru/models
• Ризниченко Г.Ю. Рубин А.Б.
Биофизическая динамика продукционных
процессов. Москва-Ижевск: Институт
компьютерных исследований. 2004. 464 с.
Как моделировать популяционную
динамику?
Численность – 100 особей
Биомасса – 4000 кг
Потребность в пище – 100 грамм травы на 1 кг биомассы в сутки
Прирост – 20 грамм на 1 кг в сутки
……………………………….
Непрерывные (популяционные) модели
 Описываются системами обыкновенных
дифференциальных уравнений
 Между особями в такой популяции нет разницы (все
идентичны)
Экспоненциальный рост
Уравнение Мальтуса
dN = rN dt
N = N0
rt
e
Мальтус
Ограничение на рост связанное
с емкостью среды
Логистическое уравнение
dN = rN (1 — (N/K)) dt
Модель Лотка - Вольтерра для системы
хищник - жертва
В природе одна популяция никогда
не может быть описана одним
уравнением, всегда есть пища (живая
или не живая) динамику которой
надо тоже описывать.
Дискретные модели
Individual based models
 Дискретные (часто с элементами стохастичности)
модели, основанные на моделировании свойств отдельных
особей.
 Требуют большей информации об объекте – много
параметров.
 Популяционная динамика = результат роста и развития
отдельных особей.
,
В чем основная проблема любой из
популяционных моделей?
В описании зависимостей скорости роста
биомассы, потребления субстрата
организмом, дыхания, выделения,
размножения и т.п.
Для моделирования трансформации
компонент экосистемы
 образование и превращение веществ
 потребление
 рост и элиминация организмов
как правило, используются наиболее
простые уравнения ферментативной
кинетики.
Уравне́ние Михаэ́ лиса —
Ме́нтен — основное
уравнение ферментативной
кинетики, описывает
зависимость скорости
реакции, катализируемой
ферментом, от
концентрации субстрата и
фермента.
Непрерывные vs. Дискретные модели
(«Корпускулярно-волновой дуализм»)
 Популяция есть сумма индивидуумов
(увеличивается дискретно).
 Популяция есть растущая биомасса (растет
непрерывно).
 Выбор подхода зависит от сложности
организма, его жизненного цикла, и задач
моделирования.
Кого и как моделировать?
 Бактерии (непрерывно).
 Водоросли (непрерывно, однако если есть
покоящиеся стадии возможно необходимо
разбивать на классы).
 Зоопланктон (иногда непрерывно, но в
настоящее время чаще дискретно или как
минимум с разбивкой на классы (возрастные и
половые группы, покоящиеся стадии).
 Рыбы (возрастные классы (когорты), чаще
дискретно).
Противоречие
 С ростом размера организма и усложнением
его жизненного цикла возникает необходимость
учета индивидуальных особенностей.
 С ростом размера модели возникает
необходимость уменьшения числа параметров –
упрощения модели конкретного звена.
Основные тенденции в моделировании
популяций это учет:
 новых механизмов потребления ресурса
(качество пищи, селективность питания)
 структурных и возрастных особенностей
популяций (особенности питания разновозрастных
особей, покоящиеся стадии)
 новых взаимодействий между популяциями
(химические, поведенческие)
 пространственных и временных неоднородностей
(миграции)