Признаки равенства прямоугольных треугольников B
реклама
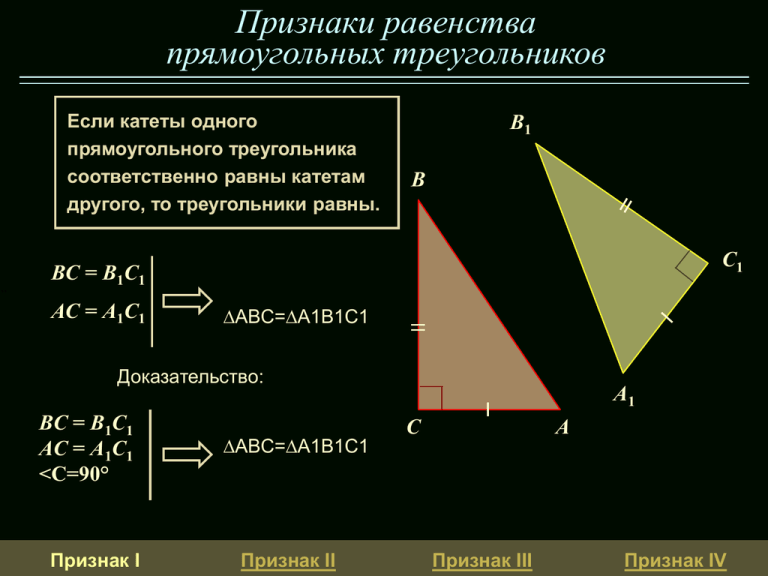
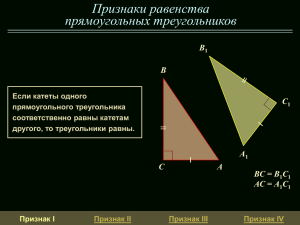
Признаки равенства прямоугольных треугольников Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то треугольники равны. „ B1 B C1 BC = B1C1 AC = A1C1 ∆ABC=∆A1B1C1 Доказательство: BC = B1C1 AC = A1C1 <С=90° Признак I ∆ABC=∆A1B1C1 Признак II A1 C A Признак III Признак IV Признаки равенства прямоугольных треугольников Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого, то треугольники равны. BC = B1C1 B = B1 ∆ABC=∆A1B1C1 B1 B C1 Доказательство: BC = B1C1 B = B1 С = С1=90° Признак I A1 C A ∆ABC=∆A1B1C1 Признак II Признак III Признак IV Признаки равенства прямоугольных треугольников Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то треугольники равны. AB = A1B1 B = B1 B ∆ABC=∆A1B1C1 B1 C1 Доказательство B = B1 А = 90- B А= А1 А 1= 90- B1 AB = A1B1 B = B1 A1 C A ∆ABC=∆A1B1C1 А= А1 Признак I Признак II Признак III Признак IV Признаки равенства прямоугольных треугольников Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то треугольники равны. ∆ABC=∆A1B1C1 AB = A1B1 BC = B1C1 B B1 Доказательство (отпротивного) Треугольник A1B1C1 можно наложить на треугольник ABC так, чтобы совместились их прямые углы и катеты B1C1 и BC. Если треугольники не совпадут, то образуется треугольник ABA2, в котором AB = A2B и в то же время один из углов при стороне AA2 (основание) тупой, а другой острый Противоречие, в равнобедренном треугольнике углы при основании равны Признак I Признак II C1 C A2 A A1 ∆ABC=∆A1B1C1 Признак III Признак IV