Рекомендации по В8 (2 лист)

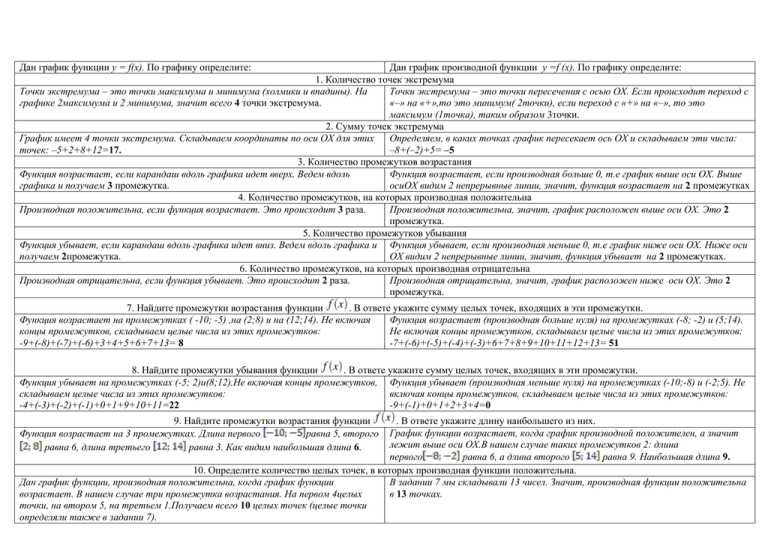
Дан график функции y = f(x). По графику определите:
Дан график производной функции y =f (x). По графику определите:
1. Количество точек экстремума
Точки экстремума – это точки максимума и минимума (холмики и впадины). На
Точки экстремума – это точки пересечения с осью ОХ. Если происходит переход с
графике 2максимума и 2 минимума, значит всего 4 точки экстремума.
«–» на «+»,то это минимум( 2точки), если переход с «+» на «–», то это
максимум (1точка), таким образом 3точки.
2. Сумму точек экстремума
График имеет 4 точки экстремума. Складываем координаты по оси ОХ для этих
Определяем, в каких точках график пересекает ось ОХ и складываем эти числа:
точек: –5+2+8+12=17.
–8+(–2)+5= –5
3. Количество промежутков возрастания
Функция возрастает, если карандаш вдоль графика идет вверх. Ведем вдоль
Функция возрастает, если производная больше 0, т.е график выше оси ОХ. Выше
графика и получаем 3 промежутка.
осиОХ видим 2 непрерывные линии, значит, функция возрастает на 2 промежутках
4. Количество промежутков, на которых производная положительна
Производная положительна, если функция возрастает. Это происходит 3 раза.
Производная положительна, значит, график расположен выше оси ОХ. Это 2
промежутка.
5. Количество промежутков убывания
Функция убывает, если карандаш вдоль графика идет вниз. Ведем вдоль графика и Функция убывает, если производная меньше 0, т.е график ниже оси ОХ. Ниже оси
получаем 2промежутка.
ОХ видим 2 непрерывные линии, значит, функция убывает на 2 промежутках.
6. Количество промежутков, на которых производная отрицательна
Производная отрицательна, если функция убывает. Это происходит 2 раза.
Производная отрицательна, значит, график расположен ниже оси ОХ. Это 2
промежутка.
7. Найдите промежутки возрастания функции
. В ответе укажите сумму целых точек, входящих в эти промежутки.
Функция возрастает на промежутках ( -10; -5) ,на (2;8) и на (12;14). Не включая
Функция возрастает (производная больше нуля) на промежутках (-8; -2) и (5;14).
концы промежутков, складываем целые числа из этих промежутков:
Не включая концы промежутков, складываем целые числа из этих промежутков:
-9+(-8)+(-7)+(-6)+3+4+5+6+7+13= 8
-7+(-6)+(-5)+(-4)+(-3)+6+7+8+9+10+11+12+13= 51
8. Найдите промежутки убывания функции
. В ответе укажите сумму целых точек, входящих в эти промежутки.
Функция убывает на промежутках (-5; 2)и(8;12).Не включая концы промежутков, Функция убывает (производная меньше нуля) на промежутках (-10;-8) и (-2;5). Не
складываем целые числа из этих промежутков:
включая концы промежутков, складываем целые числа из этих промежутков:
-4+(-3)+(-2)+(-1)+0+1+9+10+11=22
-9+(-1)+0+1+2+3+4=0
9. Найдите промежутки возрастания функции
Функция возрастает на 3 промежутках. Длина первого
равна 5, второго
равна 6, длина третьего
равна 3. Как видим наибольшая длина 6.
. В ответе укажите длину наибольшего из них.
График функции возрастает, когда график производной положителен, а значит
лежит выше оси ОХ.В нашем случае таких промежутков 2: длина
первого
равна 6, а длина второго
равна 9. Наибольшая длина 9.
10. Определите количество целых точек, в которых производная функции положительна.
Дан график функции, производная положительна, когда график функции
В задании 7 мы складывали 13 чисел. Значит, производная функции положительна
возрастает. В нашем случае три промежутка возрастания. На первом 4целых
в 13 точках.
точки, на втором 5, на третьем 1.Получаем всего 10 целых точек (целые точки
определяли также в задании 7).
11. Определите количество целых точек, в которых производная функции
отрицательна.
Дан график функции, производная отрицательна, когда график функции убывает. Производная отрицательна, когда график ниже оси ОХ. Целых точек, лежащих
В нашем случае три промежутка убывания. В задании 8 мы складывали 9 целых
ниже оси ОХ 7. Значит ответ: 7.
чисел. Значит, производная отрицательна в 9 целых точках.
12. Найдите количество точек, в которых касательная к графику функции параллельна прямой
или совпадает с ней.
Точки экстремума (максимумы и минимумы) – это точки, в которых касательная Данная прямая имеет угловой коэффициент равный 0. Прямая у = 0 (ось ОХ)
пересекает график производной функции 3раза. Ответ: 3.
параллельна прямой
. Считаем количество точек экстремума. Ответ: 4.
13. Найдите количество точек, в которых касательная к графику функции
параллельна прямой
или совпадает с ней.
Прямая
имеет угловой коэффициент равный – 2. Значит, проведем
прямую у = – 2 и посчитаем количество точек пересечения этой прямой с
графиком производной функции. Ответ: 3.
На отрезке
Ответ: -5.
14. В какой точке отрезка
функция
принимает наибольшее значение.
функция принимает наибольшее значение в точке х = - 5.
На отрезке
график производной лежит выше оси ОХ, значит,
производная положительна, а когда производная положительна график функции
возрастает. Наибольшее значение будет в точке -2.