задания скачайте здесь..

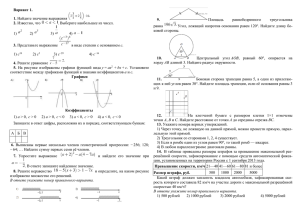
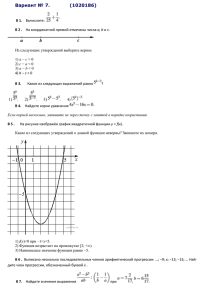
1. Найдите значение выражения
Вариант 1
30⋅ (− 0,1)3+7⋅ (− 0,1)2−3,9
2. Решите уравнение x3+2x2−x−2=0.
3. Для приготовления фарша взяли говядину и свинину в отношении 19:1.
Какой процент в фарше составляет свинина?
4. Девятиклассники Петя, Катя, Ваня, Даша и Наташа бросили жребий, кому начинать игру.
Найдите вероятность того, что начинать игру должна будет девочка.
5. Известно, что графики функций y=x2+p и y=2x−5 имеют ровно одну общую точку.
Определите координаты этой точки. Постройте графики заданных функций в одной системе
координат.
6. В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к
нему, равен 45∘ . Найдите площадь треугольника.
7. Кофейник, который стоил 900 рублей, продаётся с 10-процентной скидкой. При покупке
этого кофейника покупатель отдал кассиру 1000 рублей. Сколько рублей сдачи он должен
получить?
8. Решите неравенство (x−4)2 < 6(x−4)
Вариант 2
1. Найдите значение выражения 50⋅ (− 0,1)³ +5⋅ (− 0,1)² + 0,5
2. Решите уравнение
x²+2x−15=0
3. Для приготовления чайной смеси смешивают индийский и цейлонский чай в отношении
9:11. Какой процент в этой смеси составляет цейлонский чай?
4. Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на
стороне BC. Найдите AB, если BC=34.
5. В фирме «Чистая вода» стоимость (в рублях) колодца из железобетонных колец
рассчитывается по формуле C=6500+4000⋅ n, где n — число колец, установленных при
рытье колодца. Пользуясь этой формулой, рассчитайте стоимость колодца из 11 колец.
Ответ укажите в рублях.
6. В лыжных гонках участвуют 7 спортсменов из России, 1 спортсмен из Норвегии и 2
спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием.
Найдите вероятность того, что спортсмен из Норвегии будет стартовать последним.
7. Спортивный магазин проводит акцию: «Любая футболка по цене 300 рублей. При покупке
двух футболок — скидка на вторую 60%». Сколько рублей придётся заплатить за покупку
двух футболок?
8. Найдите p и постройте график функции y=x2+p, если известно, что прямая y=−2x имеет с
графиком ровно одну общую точку.