Парадоксы бесконечности

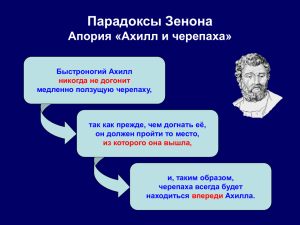
Парадоксы бесконечности.
Геометрия бесконечного завораживающа и удивительна – будь то углубление в ее
микроскопические детали или заполнение беспредельных пространств. Мысль человеческая
воспаряет от осознания своей интеллектуальной мощи, от чувства безграничности своего
распространения – и спотыкается о парадоксы, обнаруживающиеся при внимательном подходе
к проблемам бесконечности.
Вот простой и древний (еще древнегреческий) парадокс, известный под названием «Ахилл и
черепаха». Пусть в пункте A находится бегун (Ахилл), а в пункте B на некотором расстоянии от
A — черепаха. В один и тот же момент Ахилл отправляется бегом из A в направлении к B,
стремясь догнать черепаху, а черепаха устремляется из B прочь от A со скоростью, скажем, в
сто раз меньшей скорости бегуна.
Опыт свидетельствует, что в подобной ситуации Ахилл довольно быстро догонит черепаху.
С другой стороны, можно, как будто, установить, что Ахилл никогда не догонит черепаху (и
даже не достигнет пункта B).
В самом деле, к моменту, когда Ахилл достигнет середины C1 маршрута AB, черепаха пусть на
небольшое расстояние, но всё же удалится от В. Далее, Ахилл добежит до середины C2 отрезка
C1B, затем до середины C3 отрезка C2B и т. д. Всё это время черепаха будет удаляться от В.
Чтобы достигнуть B, Ахиллу, таким образом, необходимо побывать в каждом из пунктов
бесконечной последовательности C1, C2, C3,…,Cn,… Очевидно, что невозможно за конечное
время побывать в бесконечном количестве различных пунктов. Вывод - Ахилл никогда не
достигнет пункта B и не догонит черепаху.
Преодоление этого парадокса лежит либо в отказе от бесконечной делимости пространства (что
и делает квантовая теория), либо в исследовании вопроса, чем является точка В в
вышеприведенном рассуждении. А она является пределом последовательности точек Сi. Но
тогда из простых арифметических выкладок станет ясно, что время достижения Ахиллом точки
В конечно – в том же смысле, как конечен предел последовательности точек Сi. То есть, если
мы принимаем в качестве постулата бесконечную делимость пространства и времени, то
должны считать неотличимыми точку В и предел сходящейся к ней последовательности точек
Сi. Следовательно, мы должны считать неотличимыми время Т, за которое Ахилл достигнет
точки В, и предел последовательности времен Тi, за которые он достигнет точек Сi. А этот
предел конечен.
Граница между бесконечностью и нулем порой совершенно неразличима.
Чему равна сумма следующего ряда:
4 – 4 + 4 – 4 + 4 – 4 + 4 …?
Если сгруппировать его члены так:
(4 – 4 ) + ( 4 – 4 ) + ( 4 – 4 ) + … ,
то сумма равна нулю. Но если сгруппировать их иначе,
4 – ( 4 – 4) – ( 4 – 4 ) – ( 4 – 4 ) - …, то сумма равна 4.
Можно сгруппировать члены ряда еще одним способом:
4 – (4 – 4 + 4 – 4 + 4 – 4 + 4 … ).
Тогда сумма ряда будет равна 4 минус сумма такого же ряда. То есть удвоенная сумма равна 4,
поэтому сумма равна 2.
Суть этого парадокса в том, что данный ряд не сходится и его сумма колеблется между 0 и 4.
Посмотрим теперь, является ли внутренне противоречивым следующее мысленное построение.
Представим себе лампу, которая либо включена, либо нет. Начиная с некого момента она на
полминуты включена, потом 1/4 минуты выключена, потом снова 1/8 минуты включена, и т.д.
Сумма прогрессии ½+1/4+1/8+… есть 1. То есть за минуту лампа совершит счетное число
переключений. Будет ли лампа при этом гореть или нет? Бегун из парадокса “Ахилл и черепаха”
достигнет точки B за конечное время. Почему нельзя утверждать, что выключатель лампы через
минуту сработает в последний раз? Ответ заключается в том, что лампа должна после этого
остаться либо включенной, либо выключенной, а это означает то же самое, что утверждение о
существовании последнего целого числа, которое является четным или нечетным. То есть
представленная нами схема работы лампы логически абсурдна.
Бесконечность неявно может присутствовать в парадоксах, выраженных не в математических
терминах, например, семантических.
Рассмотрим множество натуральных чисел, каждое из которых может быть однозначно
определено с помощью осмысленного текста, содержащего не более тысячи слогов. Очевидно,
таких чисел — конечное количество, т. к. совокупность всех текстов с не более чем тысячью
слогами конечна. Рассмотрим наименьшее натуральное число, не входящее в упомянутое выше
множество.
Приведённый выше абзац представляет собой осмысленный текст объёмом не более чем в
тысячу слогов, однозначно определяющий некоторое натуральное число, которое по самому
своему определению не может быть охарактеризовано такого рода текстом.
Конечно, парадокса можно избежать, если объявить указанный текст неосмысленным, но тогда
естественно поставить трудные проблемы, касающиеся описания критериев осмысленности
текстов.
Парадокса можно избежать также , объявив этот же текст не определяющим натурального
числа, что ближе к математической стороне вопроса, так как в нем присутствует утверждение о
конечности множества чисел, определяемых текстом длиною менее тысячи слогов. Это
утверждение не до конца верно и зависит от того, в динамике мы рассматриваем это множество,
или в статике. Определяя искомое число как наименьшее, не входящее в множество, мы по сути
расширяем само множество, добавляя в него подходящий элемент. И так можно продолжать до
бесконечности.
Философ Евбулид из Милет сформулировал следующий парадокс. Допустим, что кто-то
произносит следующую фразу: «Высказывание, которое я сейчас произношу, ложно». Ложно
само это высказывание или нет? Пусть высказывание истинно, тогда из него следует, что оно
ложно. А отсюда немедленно следует, что оно не может быть ложно. Известно много вариантов
этого парадокса — парадокс лжеца, парадокс Эпименида и другие. Идея этого парадокса лежит
в основе доказательства знаменитой теоремы Гёделя о неполноте формальных аксиоматических
теорий.
Проявим динамическую природу этого парадокса, представив его в следующем виде. Напишем
на одной стороне бумажной карточки «Утверждение на обратной стороне этой карточки
истинно», а на обратной стороне – «Утверждение на обратной стороне этой карточки ложно»
Переворачивая карточку , зададимся тем же вопросом: “Истинно ли высказывание, которое мы
читаем?”
Как мы видим, бесконечные последовательности приводят к различным недоразумениям в
логике, семантике и других отраслях науки. Иногда просто необходимо прервать эту
последовательность. Английский математик Дж. Литлвуд привел в своей книге
«Математическая смесь» в качестве примера такой ситуации три примечания, сделанные в
конце одной из его статей. Статья была опубликована во французском журнале и примечания
(на французском языке, которого Литлвуд не знал) гласили:
1. Я весьма признателен профессору Риссу за перевод настоящей статьи.
2. Я весьма признателен профессору Риссу за перевод предыдущего примечания.
3. Я весьма признателен профессору Риссу за перевод предыдущего примечания.
С помощью какого рассуждения Литлвуд избежал необходимости повторять второе примечание
бесконечно?
Александр Э. Привалов
Ответ – Литлвуд мог переписать французский перевод второго примечания.