Контрольная работа №5, 140400 – Электроэнергетика и

КОНТРОЛЬНАЯ РАБОТА№ 5 по теме:
«Теория вероятностей и элементы математической статистики»
140400 – Электроэнергетика и электротехника (электроснабжение)
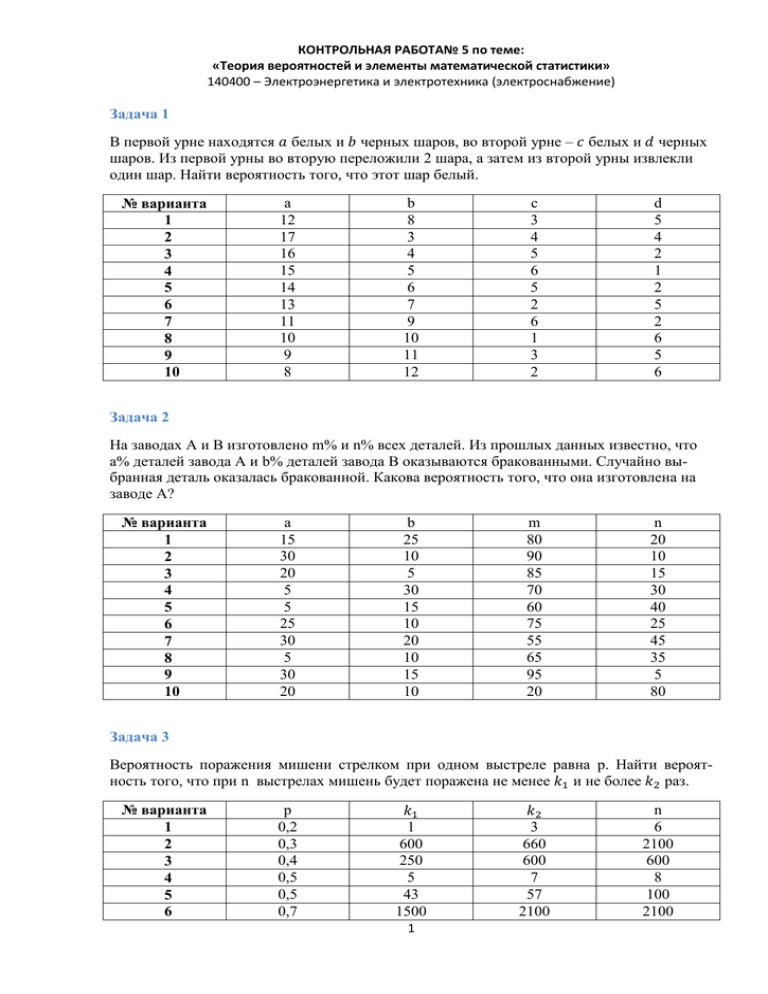
Задача 1
В первой урне находятся 𝑎 белых и 𝑏 черных шаров, во второй урне – 𝑐 белых и 𝑑 черных
шаров. Из первой урны во вторую переложили 2 шара, а затем из второй урны извлекли
один шар. Найти вероятность того, что этот шар белый.
№ варианта
1
2
3
4
5
6
7
8
9
10
a
12
17
16
15
14
13
11
10
9
8
b
8
3
4
5
6
7
9
10
11
12
c
3
4
5
6
5
2
6
1
3
2
d
5
4
2
1
2
5
2
6
5
6
Задача 2
На заводах А и В изготовлено m% и n% всех деталей. Из прошлых данных известно, что
a% деталей завода А и b% деталей завода В оказываются бракованными. Случайно выбранная деталь оказалась бракованной. Какова вероятность того, что она изготовлена на
заводе А?
№ варианта
1
2
3
4
5
6
7
8
9
10
a
15
30
20
5
5
25
30
5
30
20
b
25
10
5
30
15
10
20
10
15
10
m
80
90
85
70
60
75
55
65
95
20
n
20
10
15
30
40
25
45
35
5
80
Задача 3
Вероятность поражения мишени стрелком при одном выстреле равна p. Найти вероятность того, что при n выстрелах мишень будет поражена не менее 𝑘1 и не более 𝑘2 раз.
№ варианта
1
2
3
4
5
6
p
0,2
0,3
0,4
0,5
0,5
0,7
𝑘1
1
600
250
5
43
1500
1
𝑘2
3
660
600
7
57
2100
n
6
2100
600
8
100
2100
КОНТРОЛЬНАЯ РАБОТА№ 5 по теме:
«Теория вероятностей и элементы математической статистики»
140400 – Электроэнергетика и электротехника (электроснабжение)
0,3
0,6
0,8
0,9
7
8
9
10
3
345
86
86
6
375
100
94
6
600
100
100
Задача 4
Дискретная случайная величина принимает значения 𝑥𝑖 с вероятностями 𝑝𝑖 . Найти ее математическое ожидание, дисперсию, среднее квадратическое отклонение. Составить
функцию распределения и построить ее график.
№ варианта
1
2
3
4
5
6
7
8
9
10
𝑥1
1
4
6
3
8
3
4
4
1
8
𝑥2
5
7
2
6
7
5
7
5
2
3
𝑥3
3
1
8
7
3
7
5
6
8
4
𝑝1
0,1
0,4
0,3
0.6
0,4
0.5
0.6
0,5
0.8
0,1
𝑝2
0,7
0,5
0.2
0,3
0.2
0.1
0,2
0,3
0,1
0,5
𝑝3
0,2
0,1
0.5
0,1
0,4
0,4
0,2
0,2
0.1
0.4
Задача 5
Случайная величина X задана интегральной функцией распределения F(x). Требуется
найти дифференциальную функцию распределения, математическое ожидание, дисперсию, среднеквадратическое отклонение, построить графики интегральной и дифференциальной функций, найти вероятность попадания случайной величины X в интервал (0,1 ).
№ варианта
0, 𝑥 ≤ 2
2
𝑥 − 4𝑥 + 4
1.
𝐹(𝑥) = {
,
2<𝑥≤4
4
1, 𝑥 > 4
0, 𝑥 ≤ −1
𝑥2 + 1
2.
𝐹(𝑥) = {
, −1 < 𝑥 ≤ 3
4
1, 𝑥 > 3
0, 𝑥 ≤ 1
3
2
𝑥 − 3𝑥 + 3𝑥 − 1
3.
𝐹(𝑥) = {
,
1<𝑥≤3
4
1, 𝑥 > 3
0, 𝑥 ≤ 0
𝑥 2 + 3𝑥
4.
𝐹(𝑥) = {
,
0<𝑥≤3
18
1, 𝑥 > 3
2
КОНТРОЛЬНАЯ РАБОТА№ 5 по теме:
«Теория вероятностей и элементы математической статистики»
140400 – Электроэнергетика и электротехника (электроснабжение)
0, 𝑥 ≤ 3
𝐹(𝑥) = {
5.
𝑥−3
,
7
3 < 𝑥 ≤ 10
1, 𝑥 > 10
0, 𝑥 ≤ 2
1
2
𝐹(𝑥) = { 𝑥 − ,
2<𝑥≤7
5
5
1, 𝑥 > 7
0, 𝑥 ≤ 1
𝑥3 − 𝑥
𝐹(𝑥) = {
,
1<𝑥≤3
24
1, 𝑥 > 3
0, 𝑥 ≤ 3
2
𝑥 −𝑥−6
𝐹(𝑥) = {
,
3<𝑥≤4
6
1, 𝑥 > 4
0, 𝑥 ≤ −3
𝑥 1
𝐹(𝑥) = { + , −3 < 𝑥 ≤ 3
6 2
1, 𝑥 > 3
0, 𝑥 ≤ 0,5
2𝑥 2 − 𝑥
𝐹(𝑥) = {
,
0,5 < 𝑥 ≤ 2
6
1, 𝑥 > 2
6.
7.
8.
9.
10.
Задача 6
Для изучения количественного признака X из генеральной совокупности извлечена
выборка x1 , x2 ,..., xn объема n , имеющая данное статистическое распределение.
а) Построить полигон частот по данному распределению выборки.
б) Найти выборочное среднее xB , выборочное среднее квадратичное отклонение  B
и исправленное среднее квадратичное отклонение S .
в) При данном уровне значимости  проверить по критерию Пирсона гипотезу о
нормальном распределении генеральной совокупности.
г) В случае принятия гипотезы о нормальном распределении генеральной совокупности найти доверительные интервалы для математического ожидания a и среднего
квадратичного отклонения  при данном уровне надежности   1   .
Вариант 1:   0,01
xi
ni
4
6
7
11
10
14
13
22
16
20
19
13
22
9
25
5
14
17
18
24
22
26
26
18
30
11
34
7
Вариант 2:   0,05
xi
ni
6
5
10
12
3
КОНТРОЛЬНАЯ РАБОТА№ 5 по теме:
«Теория вероятностей и элементы математической статистики»
140400 – Электроэнергетика и электротехника (электроснабжение)
Вариант 3:   0,01
xi
ni
5
7
7
11
9
17
11
22
13
21
15
16
17
10
19
6
11
10
14
14
17
19
20
20
23
16
26
11
29
5
13
12
17
19
21
24
25
22
29
17
33
13
37
7
8
9
12
15
16
19
20
20
24
16
28
10
32
6
14
12
18
19
22
25
26
23
30
18
34
11
38
5
16
10
21
14
26
22
31
21
36
13
41
9
46
5
13
12
18
18
23
26
28
25
33
17
38
11
43
6
26
13
29
20
32
18
35
12
38
8
41
5
Вариант 4:   0,05
xi
ni
8
5
Вариант 5:   0,01
xi
ni
9
6
Вариант 6:   0,05
xi
ni
4
5
Вариант 7:   0,01
xi
ni
10
7
Вариант 8:   0,05
xi
ni
11
6
Вариант 9:   0,01
xi
ni
8
5
Вариант 10:   0,05
xi
ni
20
5
23
9
4