1. Общая нагрузка на фундамент состоит из четырех нормально распределенных

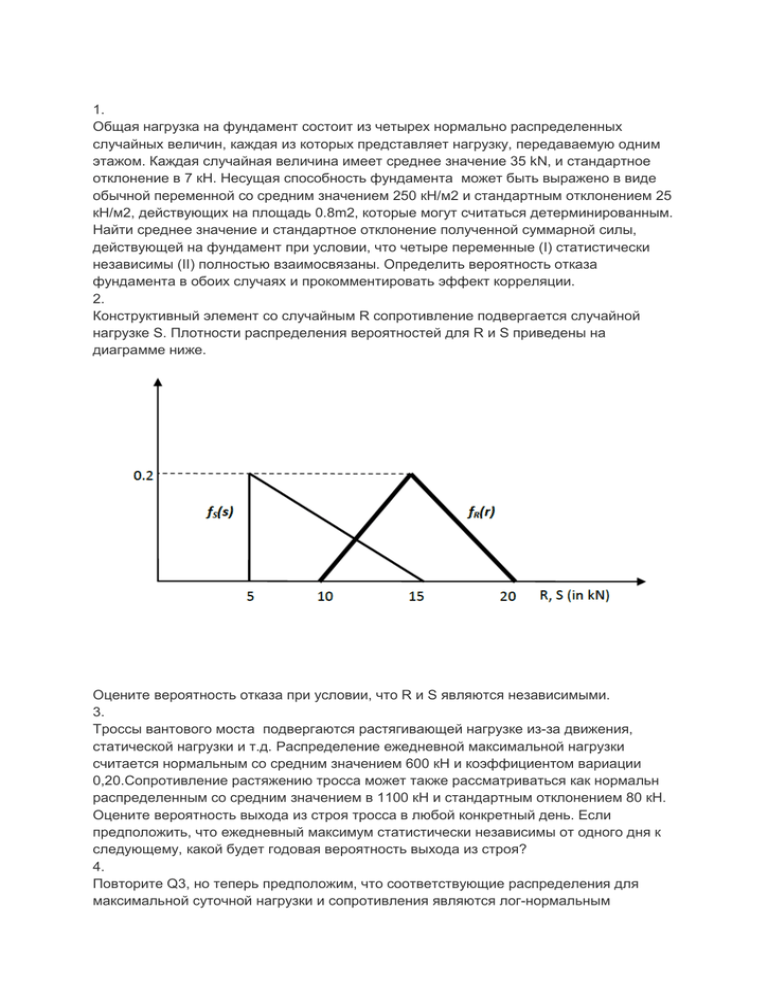
1.
Общая нагрузка на фундамент состоит из четырех нормально распределенных
случайных величин, каждая из которых представляет нагрузку, передаваемую одним
этажом. Каждая случайная величина имеет среднее значение 35 kN, и стандартное
отклонение в 7 кН. Несущая способность фундамента может быть выражено в виде
обычной переменной со средним значением 250 кН/м2 и стандартным отклонением 25
кН/м2, действующих на площадь 0.8m2, которые могут считаться детерминированным.
Найти среднее значение и стандартное отклонение полученной суммарной силы,
действующей на фундамент при условии, что четыре переменные (I) статистически
независимы (II) полностью взаимосвязаны. Определить вероятность отказа
фундамента в обоих случаях и прокомментировать эффект корреляции.
2.
Конструктивный элемент со случайным R сопротивление подвергается случайной
нагрузке S. Плотности распределения вероятностей для R и S приведены на
диаграмме ниже.
Оцените вероятность отказа при условии, что R и S являются независимыми.
3.
Троссы вантового моста подвергаются растягивающей нагрузке из-за движения,
статической нагрузки и т.д. Распределение ежедневной максимальной нагрузки
считается нормальным со средним значением 600 кН и коэффициентом вариации
0,20.Сопротивление растяжению тросса может также рассматриваться как нормальн
распределенным со средним значением в 1100 кН и стандартным отклонением 80 кН.
Оцените вероятность выхода из строя тросса в любой конкретный день. Если
предположить, что ежедневный максимум статистически независимы от одного дня к
следующему, какой будет годовая вероятность выхода из строя?
4.
Повторите Q3, но теперь предположим, что соответствующие распределения для
максимальной суточной нагрузки и сопротивления являются лог-нормальным
распределением с теми же средним и стандартным отклонениями, как указано выше.
[Подсказка: вы должны учитывать маржу, как M = R / S (> 1 для безопасности) и
использовать преобразования от логнормального к нормальному распределению.]
5.
Фундамент высотного здания может не справится из-за недостаточной
несущей способности или из-за чрезмерного проседания. Пусть B (нес.
способность) и S (осадка) представляют соответствующие события отказа
фундамента. Если P (B) = 0,001 и P (S) = 0,008 и P (B | S) = 0,1 (т.е. отказ из-за
нес. способности, вытекающий из чрезмерного проседания) определить (1)
вероятность выхода из строя фундамента ( II) вероятность того, что здание
испытает чрезмерную просадку без отказа в несущей способности.
6.
Рассмотрим оффшорные структуры, собранные с использованием большого
набора трубчатых элементов. Из испытаний, проведенных на сталелитейном
заводе, мы знаем, что вероятность того, что вязкость разрушения таких труб
превышает 50 MNm-3.2, примерно равна 1/3. Мы также установили, что в данном
случае тест на твердость будет показать значение выше 100H с вероятностью
80%. Для остальных труб с вязкостью разрушения ниже 50 MNm-3.2, вероятность
того, что тест на твердость покажет значение выше 100H составляет 30%. Если
мы получим результат твердости для конкретной трубы выше, чем 100H,
какова вероятность того, что вязкость разрушения будет выше 50 MNm-3.2?
7.
Случайная величина X имеет функцию распределения как показано ниже:
Рассчитать среднее значение  X и стандартное отклонение  X.
Убедитесь, что отношения E [X2] =  X2 +  X2.
Вывести и построить кумулятивное распределение функции FX (х).
8.
Деревянные балки были протестированы для определения значения
прочности, модуля упругости и плотности. Результаты приведены ниже.
(1) Оцените среднее и стандартное отклонение для каждого из трех свойств.
Постройте их соответствующих гистограммы.
(2) Создать графики, чтобы проиллюстрировать возможные корреляции между
тремя свойствами. Рассчитайте соответствующие коэффициенты корреляции и
обсудите их значение.
(3) Полагая, что модуль Юнга может быть описан с помощью нормального
распределения, найти значение, которое соответствует превышению в 95%.