В научный обиход термин «статистика» ввел немецкий ученый Готфрид Ахенваль в
advertisement

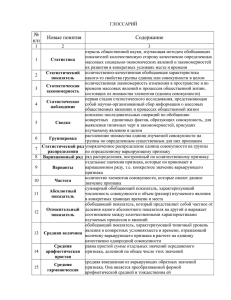
Лекция 1 1.1.Таможенная статистика. Основные понятия В научный обиход термин «статистика»1 ввел немецкий ученый Готфрид Ахенваль в 1746 году, предложив заменить название курса «Государствоведение», преподававшегося в университетах Германии, на «Статистику», положив тем самым начало развитию статистики как науки и учебной дисциплины. Несмотря на это, статистический учет велся намного раньше: проводились переписи населения в Древнем Китае, осуществлялось сравнение военного потенциала государств, велся учет имущества граждан в Древнем Риме и пр. У истоков статистической науки стояли 2 школы: немецкая описательная и английская школа политических арифметиков. Представители описательной школы (Герман Конринг, Готфрид Ахенваль, Август Людвиг Шленцер) своей задачей считали описание достопримечательностей государства: территории, населения, климата, политического устройства, вероисповедания, торговли и т.п. – без анализа закономерностей и связей между явлениями. Представители школы политических арифметиков (Уильям Петти, Джон Граунт, Эдмунд Галлей) своей главной задачей считали выявление на основе большого числа наблюдений различных закономерностей и взаимосвязей в изучаемых явлениях. Однако представители этих двух школ не дошли до теоретического обобщения практики учетно-статистических работ, до создания теории статистики. Эта задача была решена позднее, в XIX веке бельгийским ученым Адольфом Кетле, который дал определение предмета статистики, раскрыл суть ее методов. Под влиянием идей Кетле возникло третье направление статистической науки – математико-статистическое. Как и любая другая наука, статистика имеет свой предмет и метод исследования. Статистика изучает количественную сторону массовых общественных явлений в неразрывной связи с их качественной стороной или содержанием, а также исследует количественное выражение закономерностей общественного развития в конкретных условиях места и времени. Такое изучение основывается на системе категорий и понятий, отражающих наиболее общие и существенные свойства, признаки, связи и отношения предметов и явлений объективного мира. Для изучения количественной стороны явлений и систем применяются различные методы количественного анализа экономики: математическая статистка, эконометрика, финансовая математика и пр. Для проведения статистического исследования необходима информация. 1.2. Таможенная статистика Объектом изучения таможенной статистики являются внешняя торговля РФ и деятельность таможенных органов. Цель таможенной статистики – обеспечение руководства Федеральной таможенной службы (ФТС), органов законодательной и исполнительной власти информацией о 1 От лат. status – состояние, положение вещей; первоначально термин употреблялся в значении «политическое состояние» 1 состоянии и развитии внешней торговли Российской Федерации (РФ) и о деятельности таможенных органов. Соответственно определены 2 раздела таможенной статистики: таможенная статистика внешней торговли и специальная таможенная статистика (рис 1). Откуда берётся таможенная статистика? Из данных о внешнеторговых сделках, грузах, декларациях, которые с таможенных постов собирают централизованно в ФТС и образуют единую базу данных. В результате статистического наблюдения должна быть получена объективная, сопоставимая, полная информация, позволяющая на последующих этапах исследования обеспечить научно-обоснованные выводы о характере и закономерностях развития изучаемого явления. Качество и достоверность статистической информации определяют эффективность использования статистики в любой сфере. Рис.1.Виды таможенной статистики 1.3. Статистическое наблюдение. Исходная информация для статистического исследования конкретного массового явления поступает в процессе статистического наблюдения. Статистическое наблюдение представляют собой специальным образом организованный сбор сведений в виде числовых показателей о состоянии наблюдаемого объекта. Собранные статистические данные подвергаются статистической обработке, включающей проверку данных, приведение их к сопоставимому виду, систематизацию и группировку данных. Полученные результаты представляются в виде статистических таблиц, графиков. диаграмм и пр. Статистические таблицы являются наиболее рациональной и наглядной формой представления массовых данных. 2 Все многообразие форм, видов и способов наблюдения можно представить следующим образом: По форме организации статистического наблюдения: отчетность; специально организованное статистическое обследование(например,- перепись); регистры. По видам статистического наблюдения: а) по времени регистрации фактов (текущее (непрерывное); прерывное (периодическое, единовременное); б) по охвату единиц совокупности (сплошное; выборочное и т.д ) По способам получения статистической информации: непосредственное наблюдение; документальный способ; опрос и т.д . Таким образом, статистическая информация — это первичные данные о состоянии социально-экономических явлений и процессов, формирующиеся в процессе статистического наблюдения, которые затем подвергаются систематизации, сводке, анализу и обобщению. Состав информации во многом определяется потребностями исследователя и рассматриваемой предметной областью: социально – экономическая статистика, финансовая статистика, таможенная статистика и пр. В результате статистического наблюдения должна быть получена объективная, сопоставимая, полная информация, позволяющая на последующих этапах исследования обеспечить научно-обоснованные выводы о характере и закономерностях развития изучаемого явления. Качество и достоверность статистической информации определяют эффективность использования статистики в любой сфере. Статистические данные, получаемые в статистических наблюдениях, обычно подразделяют на три типа: перекрестные данные (пространственные); временные ряды; панельные (перекрестно – временные). Перекрестные данные – это данные, собранные с разных объектов в один момент времени. Временные ряды – данные для одного объекта в различные моменты времени. Нередко исходная статистическая совокупность образуется из комбинированных перекрестно–временных данных (панельные данные), например данных ряда предприятий за несколько отчетных периодов. Способы и методы изучения и обобщения полученной статистической информации практически не зависят от изучаемой предметной области. 1.4. Понятие статистической совокупности Общей целью статистического наблюдения является получение достоверной информации о тенденциях развития явлений и процессов для последующего принятия управленческих решений. Эта информация должна быть конкретной и четкой. Нечетко поставленная цель может привести к сбору не тех данных, которые необходимы для решения конкретной задачи. Цель определяет объект статистического наблюдения. Объектом любого статистического исследования является статистическая совокупность. 3 Статистическая совокупность - группа, состоящая из множества относительно однородных элементов, взятых вместе в известных границах пространства и времени и обладающих признаками сходства и различия (группа физических лиц (население, работники), юридических лиц (предприятия, фирмы, учебные заведения), физических единиц (производственное оборудование, средства передвижения и транспортировки, жилые дома) и т.д. Каждая статистическая совокупность состоит из отдельных единиц (отдельных единиц наблюдения). Единица наблюдения - каждый первичный элемент, составляющий статистическую совокупность и являющийся носителем признаков, подлежащих учету. Единица наблюдения определяется целью и задачами статистического исследования, а также избранным объектом изучения Свойства статистической совокупности: Статистическая совокупность характеризуется следующими свойствами: 1. Неразложимость. Когда появляются или исчезают какие-то элементы статистической совокупности, ее качественная основа при этом не разрушается. 2. Однородность. Статистическая совокупность всегда имеет как минимум один общий признак для всех ее элементов. И в то же время это свойство не является одинаковым для них. Этот признак может иметь разные значения для разных единиц. То, насколько статистическая совокупность однородна, устанавливается во время исследования. И зависит это свойство, прежде всего, от тех целей и задач, с которыми оно проводится. 3. Вариация. Это свойство важнее, чем два предыдущих. Оно проявляется следующим образом: во время перехода от одного элемента статистической совокупности к другому происходит изменение количественного значения признака. 4. определенные границы пространства и времени изучаемого явления Различают два вида статистической совокупности: 1). Генеральная совокупность - совокупность, состоящая из всех единиц наблюдения, которые могут быть к ней отнесены в соответствии с целью исследования. Генеральной совокупностью называют совокупность всех мыслимых наблюдений (или всех мыслимых объектов интересующего нас типа, с которых снимаются наблюдения), которые могли бы быть произведены при данном реальном комплексе условий [1]. Понятие генеральной совокупности – это понятие условно-математическое, абстрактное, и его не следует смешивать с реальными совокупностями, подлежащими статистическому исследованию. Так, обследовав даже все предприятия некоторой отрасли с точки зрения регистрации значений исследуемых показателей, мы можем рассматривать обследованную совокупность лишь как представителя гипотетически возможной более широкой совокупности предприятий, которые могли бы функционировать в рамках того же реального комплекса условий. 2). Выборочная совокупность - часть генеральной, отобранная специальным (выборочным) методом и предназначенная для характеристики генеральной совокупности. В статистических исследованиях имеют дело с выборками из генеральной совокупности – это некоторое ограниченное множество реально наблюдаемых объектов генеральной совокупности, которое можно рассматривать как эмпирический аналог генеральной совокупности. 4 Основные свойства и характеристики выборки, называемые эмпирическими (выборочными), могут быть проанализированы и найдены по имеющимся выборочным статистическим данным. Основные свойства и характеристики генеральной совокупности называют теоретическими. Они не известны исследователю и не могут быть рассчитаны, а лишь оценены по данным выборки с помощью методов математической статистики. Главное требование, предъявляемое к выборке, – ее репрезентативность (представительность), т.е. полнота и адекватность представления ею интересующих исследователя свойств генеральной совокупности. Будучи неверно определенной, выборка повлечет неверные выводы. Например, исследуя в регионе спрос на некоторую группу товаров в зависимости от доходов и включив в выборку только семьи с высоким уровнем дохода, явно получим неверные результаты. Если рассматривать величину дохода как случайную переменную, то репрезентативной выборка будет в том случае, если соответствующие относительные частоты этой величины в генеральной совокупности и в выборке будут примерно одинаковы. Существуют различные методы получения репрезентативных выборок. При условии объективности выборки необходимо иметь достаточно большую совокупность статистических наблюдений, Ошибки наблюдения и выборки Информация, полученная в ходе статистического наблюдения может не отвечать действительности, а расчетные значения показателей не соответствовать фактическим значениям, т.е. собранные данные могут содержать различные ошибки В зависимости от причин возникновения различают: ошибки регистрации и передачи информации, случайные ошибки, ошибки репрезентативности, вызванные неполным охватом наблюдениями всех единиц генеральной совокупности. Ошибки регистрации — представляют собой отклонения между значением показателя, полученного в ходе статистического наблюдения, и его фактическим значением. Ошибки репрезентативности — возникают, когда отобранная совокупность недостаточно точно воспроизводит свойства и пропорции генеральной совокупности. Случайные ошибки — являются результатом действия случайных факторов. 1.5. Статистические показатели Статистическая информация всегда представлена совокупностью показателей. Показатель как информационная единица – это качественно определенная величина, дающая количественную характеристику отображаемому объекту (предмету, процессу, явлению), имеющая экономический смысл, т.е. показатель всегда содержит количественный признак и набор качественных признаков, его определяющих. В соответствии с определением показатель имеет определенную структуру, в нем различают качественную и количественную стороны. Качественная сторона показателя определяется признаками, которые подлежит изучению и отражается в названии показателя, количественная сторона определяется- в численном значении показателя. Еще одной особенностью статистических показателей является то, что они всегда привязаны к конкретным обстоятельствам места и времени. 5 Требования к статистическим показателям: Главнейшим требованием статистики является требование обеспечения сопоставимости показателей, так как без сопоставимости нет сравнения, а значит, нет объективных выводов об изучаемом социально-экономическом явлении или процессе: показатели должны обладать общим содержанием; статистические показатели должны выражаться в одинаковых единицах измерения; сравниваемые показатели должны рассчитываться по единой методике; сравниваемые статистические показатели должны быть однородными по времени и территории – они должны определяться за одинаковые периоды времени, на одни и те же даты, по одной территории Классификация статистических показателей 1. Статистический показатель может относиться: к отдельному явлению (объекту), например к отдельному промышленному предприятию; к группе объектов одного и того же вида, например к совокупности предприятий определенной отрасли; ко всей совокупности явлений, например ко всему хозяйству страны. В соответствии с этим показатели подразделяются на индивидуальные, групповые (частные) и общие. Последние две категории называют сводными показателями. 2.Статистические показатели могут быть абсолютными или относительными. Абсолютные показатели Абсолютные показатели выражаются в натуральных, стоимостных, трудовых измерителях ( экспорт нефти в млн. баррелей, млн. рублей или $ и т.д.). Абсолютные показатели могут быть только именованными числами, где единица измерения выражается в конкретных цифрах. Абсолютные показатели следует также подразделить на моментные и интервальные: Моментные абсолютные показатели характеризуют факт наличия явления или процесса, его размер (объем) на определенную дату времени. Интервальные абсолютные показатели характеризуют итоговый объем явления за тот или иной период времени (например, выпуск продукции за квартал или за год и т. д.), допуская при этом последующее суммирование. Абсолютные показатели не могут дать исчерпывающего представления об изучаемой совокупности или явлении, поскольку не могут отразить структуру, взаимосвязи, динамику. Данные функции выполняют относительные показатели, которые определяются на основе абсолютных показателей. Относительные показатели В статистике относительные показатели используют в сравнительном анализе, в обобщении и синтезе. Относительные показатели - есть результат сопоставления двух статистических величин. Относительные показатели могут быть получены или как 6 соотношения одноименных статистических показателей, или как соотношения разноименных статистических показателей. В первом случае получаемый относительный показатель рассчитывается в процентах или в относительных единицах. Если соотносятся разноименные абсолютные показатели, то относительный показатель в большинстве случаев бывает именованным. Относительные показатели (величины), используемые в статистической практике: относительный показатель структуры; относительный показатель координации; относительный показатель планового задания; относительный показатель выполнения плана; относительный показатель динамики; относительный показатель сравнения; относительный показатель интенсивности. Относительный показатель структуры (ОПС) характеризует структуру совокупности, определяет долю (удельный вес) части в общем объеме совокупности. ОПС рассчитывают как отношение объема части совокупности к абсолютной величине всей совокупности, определяя тем самым удельный вес части в общем объеме совокупности (%): m ОПС i 100% M где mi - объем исследуемой части совокупности; M - общий объем исследуемой совокупности. Относительный показатель координации (ОПК) характеризует соотношение между двумя частями исследуемой совокупности, одна из которых выступает как база сравнения (%): m ОПK i 100% mb где mi - одна из частей исследуемой совокупности; mb - часть совокупности, которая является базой сравнения. Относительный показатель планового задания (ОППЗ) используется для расчета в процентном отношении увеличения (уменьшения) величины показателя плана по сравнению с его базовым уровнем в предшествующем периоде, для чего используется формула: Ppl 100% ОППЗ = P0 где Ppl - плановый показатель; Р0 - фактический (базовый) показатель в предшествующем периоде. Относительный показатель выполнения плана (ОПВП) характеризует степень выполнения планового задания за отчетный период (%) и рассчитывается по формуле; Pf ОПВП= 100% Ppl 7 где P f – величина выполнения плана за отчетный период; Ppl – величина плана за отчетный период. Относительный показатель динамики (ОПД) характеризует изменение объема одного и того же явления во времени в зависимости от принятого базового уровня. ОПД рассчитывают как отношение уровня анализируемого явления или процесса в текущий момент времени к уровню этого явления или процесса за прошедший период времени. В результате мы получаем коэффициент роста. При исчислении этой величины в процентах (результат умножается на 100) получаем темп роста. Темпы роста можно просчитывать как с постоянным базовым уровнем (базисные темпы роста – ОВДb ), так и с переменным базовым уровнем (цепные темпы роста - ОПДц ): Yt 100% Y b ОПДb= где Yt - уровень текущий; Yb - уровень базисный; ОПДц = Yt Yt 1 где Yt - уровень текущий; Y t 1 – уровень, предшествующий текущему. ТЕМП ПРИРОСТА — отношение абсолютного прироста показателя к уровню показателя, принятому за базу сравнения. Абсолютный прирост выражает абсолютную скорость изменения ряда динамики и определяется как разность между данным уровнем и уровнем, принятым за базу сравнения. Абсолютный прирост (базисный): tb Yt Yb где Yt - уровень сравниваемого периода; Yb - уровень базисного периода. Абсолютный прирост с переменной базой (цепной), который называют скоростью роста: tц Yt Yt 1 где Yt - уровень текущий; Y t 1 – уровень, предшествующий текущему. Темп прироста можно рассчитать и иным путем: как разность между темпом роста и 100 % или как разность между коэффициентом роста и 1 (единицей). Относительный показатель сравнения (ОПСр) - соотношение одноименных абсолютных показателей, относящихся к разным объектам, но к одному и тому же времени (например, соотносятся темпы роста населения в разных странах за один и тот же период времени): 8 Mk 100% M l ОПСр= где МK - показатель первого одноименного исследуемого объекта; МL - показатель второго одноименного исследуемого объекта (база сравнения). Все предыдущие показатели относительных величин характеризовали соотношения одноименных статистических объектов. Однако есть группа относительных величин, которые характеризуют соотношение разноименных, но связанных между собой статистических показателей. Эту группу называют группой относительных показателей интенсивности (ОПИ), которые выражаются, как правило, именованными числами. В статистической практике относительные величины интенсивности применяются при исследовании степени объемности явления по отношению к объему среды, в которой происходит распространение этого явления. ОВИ здесь показывает, сколько единиц одной совокупности (числитель) приходится на одну, на десять, на сто единиц другой совокупности (знаменатель). Примерами относительных величин интенсивности могут служить показатели уровня технического развития производства, уровня благосостояния граждан, показатели обеспеченности населения средствами массовой информации, предметами культурнобытового назначения и т.д. ОПИ рассчитывается по формуле: ОПИ= A BA где А - распространение явления; ВА - среда распространения явления А. При расчете относительных величин интенсивности может возникнуть проблема выбора адекватной явлению базы сравнения (среды распространения явления). Например, при определении показателя плотности населения нельзя брать в качестве базы сравнения общий размер территории того или иного государства, в этом случае базой сравнения может быть лишь территория в 1 км2. Критерием правильности расчета является сопоставимость по разработанной методологии расчета сравниваемых показателей, применяющихся в статистической практике. Разновидностью относительных величин интенсивности являются относительные впоказатели уровня экономического развития. ОПУЭР — характеризуют размеры производства в расчете на душу населения. Они играют важную роль в оценке развития экономики страны. Для их вычисления необходимо годовой объем производства продукции разделить на среднегодовую численность населения за тот же год. Например, размер ВВП на душу населения и пр. ) 1.6. Понятие статистических рядов распределения. Статистический ряд распределения – это упорядоченное распределение единиц совокупности на группы по определённому варьирующему признаку. Вариация определяет различия в значениях какого либо признака из разных единиц совокупности в один и тот же 9 период (момент времени). Вариация характерна всем без исключения явлением природы и общества. Исследование вариации позволяет понять сущность изучаемого явления В зависимости от признака, положенного в основу образования ряда распределения, различают атрибутивные и вариационные ряды распределения. Если за основу группировки взят качественный признак, то такой ряд распределения называют атрибутивным (распределение по видам труда, по полу, по профессии, по религиозному признаку, национальной принадлежности и т.д.). Если ряд распределения построен по количественному признаку, то такой ряд называют вариационным. Построить вариационный ряд - значит упорядочить количественное распределение единиц совокупности по значениям признака, а затем подсчитать числа единиц совокупности с этими значениями (построить групповую таблицу). Выделяют три формы вариационного ряда: ранжированный ряд, дискретный ряд и интервальный ряд. Ранжированный ряд - это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Ранжирование позволяет легко разделить количественные данные по группам, сразу обнаружить наименьшее и наибольшее значения признака, выделить значения, которые чаще всего повторяются. Дискретный ряд - это такой вариационный ряд, в основу построения которого положены признаки с прерывным изменением (дискретные признаки). К последним можно отнести тарифный разряд, количество детей в семье, число работников на предприятии и т.д. Эти признаки могут принимать только конечное число определенных значений. Дискретный вариационный ряд представляет таблицу, которая состоит из двух граф. В первой графе указывается конкретное значение признака (варианта), а во второй - число единиц совокупности с определенным значением признака (частота). Вариантами считаются отдельные значения признака, которые он принимает в вариационном ряду. Частоты f i – это число отдельных вариантов или каждой группы вариационного ряда, т.е. это числа, показывающие, как часто встречаются те или иные варианты в ряду распределения. Сумма всех частот определяет численность всей совокупности, её объём ( n ) Если признак имеет непрерывное изменение (размер дохода, стаж работы, стоимость основных фондов предприятия и т.д., которые в определенных границах могут принимать любые значения), то для этого признака нужно строить интервальный вариационный ряд. Групповая таблица здесь также имеет две графы. В первой указывается значение признака (варианты) в интервале «от - до», во второй - число единиц, входящих в интервал (частота). Очень часто таблица дополняется графой, в которой подсчитываются накопленные частоты S, которые показывают, какое количество единиц совокупности имеет значение признака не большее, чем данное значение. Частоты ряда f могут дополняться частостями w, выраженными в относительных числах (долях или процентах). Они представляют собой отношения частот каждого f интервала к их общей сумме, т.е.: wi i . fi i Статистический анализ вариационных рядов требует не только наличия единичных частот (частостей), но и накопленных частот (частостей). Накопленная частота для той или 10 иной варианты представляет собой сумму частот всех предшествующих вариант (интервалов). Пусть x – некоторое численное значение признака X. Тогда количество вариант, значения которых меньше x , называется накопленной частотой, т.е. f x f i xi x Отношение накопленной частоты к общему числу наблюдений п называется f накопленной частостью: w x i n При построении вариационного ряда с интервальными значениями, прежде всего необходимо установить величину интервалов. Интервальный вариационный ряд иногда строится с равными интервалами а иногда с неравными. При построении интервального ряда с непрерывной вариацией верхняя граница каждого интервала обычно является нижней границей последующего (20-25, 25-30, 30-35 и т.д.), а в построении интервального ряда по дискретному признаку границы смежных интервалов не повторяются (1-5 дней, 6-10 дней, 11-15 дней и т.д.). Если интервалы имеют одинаковую длину, то длина интервала R определяется как отношение размаха вариации R к числу групп m: t , где R x max xmin m Число групп произвольно , исходя из сущности m определяется исследователем исследования либо рассчитывается по специальным формулам(например , формула Стерджесса; m = 1 + 3,322 lgn, где n - общее число единиц совокупности. Общий вид дискретного вариационного ряда показан в следующей таблице Варианты Частоты f i xi x1 x2 … xm fi f 2i … fm Построение интервального вариационного ряда 1. Разбивают множество значений вариант на полуинтервалы ai , ai 1 т.е. производят их группировку. Длину и число интервалов выбирают в зависимости от целей исследования и сущности проблемы. Рекомендуется количество интервалов k выбирать по формуле Стерджерса k 1 1, 4 ln n Длина интервала равна: = U= (xmax – xmin)/ k Замечание 1. В литературе предлагается и такая форма записи формулы Стерджерса: Рекомендуемое число интервалов k 1 3,322 lg n . 2.Строим интервал: за начало 1-го интервала берут: xнач xmin U 2 2. Считают число вариант, попавших в полуинтервал ai , ai 1 . Получают значения частот f i , i 1, k . 11 3. Интервальный ряд можно представить таблицей (табл. 1.2): Варианты xi a1, a2 Частоты f i a2 , a3 fi ak , ak 1 … f 2i … fk Замечание 2. Если варианта находится на границе интервала, то ее присоединяют к правому интервалу. 1.7. Показатели статистических рядов 1.7.1 Средние величины(степенные) Средние показатели являются наиболее распространённой формой статистических показателей, используемых в социально-экономических исследованиях. Средним называется обобщающий показатель статистической совокупности, характеризующий наиболее типичный уровень явления. Он выражает величину признака, отнесённую к единице совокупности. Особенности средних показателей заключаются в том, что они, во-первых, отражают то общее, что присуще всем единицам совокупности; во-вторых, в них взаимопогашаются те отклонения значений признака, которые возникают под воздействием случайных факторов. Это означает, что средний показатель отражает типичный уровень признака, формирующийся под воздействием основных доминирующих неслучайных факторов. Применение средних величин позволяет охарактеризовать определенный признак совокупности одним числом, несмотря на то, что у разных единиц совокупности значения признака отличны друг от друга. В социально-экономическом анализе используются два класса средних величин: - степенные средние; - структурные средние. К степенным средним относятся несколько видов средних, построенных по одному n общему принципу: X k xik i 1 , где xi значение варианты, n объем совокупности n k показатель степени, который может принимать любые значения, но на практике обычно используются несколько его значений: при k = 1 получают среднюю арифметическую; при k = -1 – среднюю гармоническую; при k =2 – среднюю квадратическую. Средняя обозначается через . Черта вверху символизирует процесс осреднения индивидуальных значений. 12 Если исходные данные представлены простым перечислением значений признака у статистических единиц, то используется формула средней простой. Если данные предварительно сгруппированы (представлены рядом распределения), то используется формула степенной средней взвешенной: n xik f i X k i 1 n fi i 1 Для того, чтобы средний показатель был действительно типизирующим, он должен рассчитываться с учетом определенных принципов: Средняя должна определяться для совокупностей, состоящих из качественно однородных единиц. Средняя должна исчисляться для совокупности, состоящей из достаточно большого числа единиц. Средняя должна рассчитываться для совокупности, единицы которой находятся в нормальном, естественном состоянии. Средняя должна вычисляться с учетом экономического содержания исследуемого показателя. Средняя арифметическая Средняя арифметическая является наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. При этом если индивидуальные значения признака у статистических единиц заменить средней арифметической, то суммарный объем признака по совокупности в целом сохраняется неизменным. Это означает, что средняя арифметическая есть среднее слагаемое. Средняя арифметическая простая используется при работе с несгруппированными данным и и рассчитывается по формуле: n xi X i 1 . n Формулу можно получить из общей формулы степенных средних при k 1 Пример. Известна сменная выработка рабочих бригады токарей: табельный номер рабочего 1 2 3 4 5 количество изготовленных деталей, шт. 21 19 20 18 21. Требуется определить среднюю выработку бригады. Для ее нахождения используется формула средней арифметической простой: Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным или вариационным рядам. В 13 подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднюю сгруппированных величин: n xi f i X i 1 i f i или n X xi wi , где wi i 1 fi ,где wi частость вариационного fi i признака. Свойства средней арифметическойй Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся: 1. Средняя арифметическая постоянной величины равна этой величине: A A при А=const; 2 . Алгебраическая сумма отклонений вариант от их средней арифметической равно нулю: ( xi x ) f i 0 i 3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя ( xi A) f i арифметическая из них уменьшится (увеличится) на это же число: i xA n 4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз: ( xi A) f i i xA n 5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится. n f xi ( i A ) X i 1 f i ( i A ) Средняя гармоническая Средняя гармоническая имеет более сложную конструкцию, чем средняя арифметическая. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1. n x gar 1 i xi Средняя гармоническая используется тогда, когда статистическая информация не содержит данных о весах по отдельным вариантам совокупности, но известны произведения значений варьирующего признака на соответствующие им веса U i 14 Общая формула средней гармонической взвешенной имеет следующий вид: ui x gar i u i i xi ,где xi – величина варьирующего признака, ui f i xi –– произведение значения варьирующего признака на его веса (частоты) Например, три партии товара А куплены по разным ценам (20, 25 и 40 руб.) Общая стоимость первой партии составила 2000 руб., второй партии – 5000 руб., и третьей партии – 6000 руб. Требуется определить среднюю цену единицы товара А. Средняя цена определяется как частное от деления общей стоимости на общее количество закупленного товара. Используя среднюю гармоническую, мы получим искомый результат: В том случае, если общие объемы явлений, т.е. произведения значений признаков на их веса равны, то применяется средняя гармоническая простая: Пример. Две машины прошли один и тот же путь: одна со скоростью 60 км/час, а вторая – 80 км/час. Принимаем протяженность пути, который прошла каждая машина, за единицу. Тогда средняя скорость составит: Средняя квадратическая Средняя квадратическая используется в тех случаях, когда при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин. Главная сфера её использования – измерение степени колеблемости индивидуальных значений признака относительно средней арифметической (среднее квадратическое отклонение). Может быть получена из общей формлы степенных средних при k = 2 Кроме этого, средняя квадратическая применяется в тех случаях, когда необходимо вычислить среднюю величину признака, выраженного в квадратных или кубических единицах измерения (при вычислении средней величины квадратных участков, средних диаметров труб, стволов и т. д.). n xi2 Средняя квадратическая простая рассчитывается по формуле: X i 1 n , средняя n xi2 f i квадратическая взвешенная по формуле: X i 1 i f i 15 Средняя геометрическая Средняя геометрическая применяется в тех случаях, когда общий объем усредняемого признака является мультипликативной величиной, т.е. определяется не суммированием, а умножением индивидуальных значений признака. Форма средней геометрической взвешенной в практических расчётах не применяется. В социально-экономических исследованиях средняя геометрическая применяется в анализе рядов динамики при определении среднего коэффициента роста, когда задана последовательность относительных величин динамики. Средняя геометрическая используется также для определения равноудаленной величины от максимального и минимального значения признака Все степенные средние различаются между собой значениями показателя степени. При этом, чем выше показатель степени, тем больше количественное значение среднего показателя Это свойство степенных средних называется свойством мажорантности средних. Таким образом, выбор вида среднего показателя оказывает существенное влияние на его численную величину. Выбор вида средней определяется в каждом отдельном случае путем анализа исследуемой совокупности и изучения содержания явления. Степенная средняя выбрана правильно, если на всех этапах вычислений не меняется её логическая формула, т.е.реально сохраняется социально-экономическое содержание усредняемого признака. Виды степенных средних Название средней арифметическая гармоническая Показатель Формула расчета степени Простая n 1 xi X i 1 n –1 x gar n 1 i xi Взвешенная n xi f i X i 1 i f i ui x gar i u i i xi ,где ui f i xi квадратическая 2 n xi2 X i 1 n n xi2 f i X i 1 i f i геометрическая 16 Структурные средние Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены, в основном, модой и медианой. Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле: где: — значение моды — нижняя граница модального интервала — величина интервала — частота модального интервала — частота интервала, предшествующего модальному — частота интервала, следующего за модальным Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части. Для определения медианы в fi дискретном ряду при наличии частот сначала вычисляют полусумму частот i , а затем 2 определяют, какое значение варианты приходится на нее. Если отсортированный ряд содержит нечетное число признаков, то номер медианы n 1 вычисляют по формуле: , в случае четного числа признаков медиана будет равна 2 средней из двух признаков находящихся в середине ряда. При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле: 17 где: — искомая медиана — нижняя граница интервала, который содержит медиану — величина интервала — сумма частот или число членов ряда - сумма накопленных частот интервалов, предшествующих медианному — частота медианного интервала Пример. Найти моду и медиану. Возрастные группы Число студентов Сумма накопленных частот ΣS До 20 лет 346 346 20 — 25 872 1218 25 — 30 1054 2272 30 — 35 781 3053 35 — 40 212 3265 40 — 45 121 3386 45 лет и более 76 3462 Итого 3462 Решение: В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на этот интервал приходится наибольшая частота (1054). Рассчитаем величину моды: Это значит что модальный возраст студентов равен 27 годам. Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта, которая делит совокупность на две равные части (Σfi/2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы: 18 Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года. Характеристики рассеяния вариационного ряда Степень близости индивидуальных значений к средней измеряется абсолютными, средними и относительными величинами: 1) Размах вариации: X max X min . Он характеризует лишь наибольшие различия значений признака, но не измеряет вариацию во всей совокупности. 2) Среднее линейное отклонение. Среднее линейное отклонение d представляет собой среднюю арифметическую абсолютных значений отклонений отдельных вариантов от их средней арифметической. Среднее линейное отклонение: xi x для несгруппированных данных d i , где n — число членов ряда; n xi x f i для дискретного ряда d i , fi i xi* x f i интервального ряда d i fi , где — f i сумма частот вариационного i i ряда, xi* – середина i – го интервала. Порядок расчёта среднего линейного отклонения в интервальном ряду распределения следующий: 1. Вычисляется средняя арифметическая взвешенная для интервального ряда. 2. Определяются абсолютные отклонения срединных вариант от найденной средней взвешенной: 3. Полученные отклонения умножаются на частоты: 4. Находится сумма взвешенных отклонений без учёта знака: 5. Сумма взвешенных отклонений делится на сумму частот: В формулах линейного отклонения разности взяты по модулю, иначе алгебраическая сумма отклонений вариантов от их средней арифметической равна нулю. Поэтому среднее линейное отклонение как меру вариации признака применяют в статистической практике редко (только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл). С его помощью, например, анализируется состав работающих, ритмичность производства, оборот внешней торговли. 19 Дисперсия В качестве меры рассеяния вариационного ряда чаще используются выборочная дисперсия и среднеквадратичное отклонение. Дисперсия признака представляет собой средний квадрат отклонений вариантов от их средней величины, она вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных): для несгруппированных данных: для дискретного вариационного ряда: ; интервального вариационного ряда . Приведем два из них: 1. Если все значения признака уменьшить или увеличить на одну и ту же постоянную величину , то дисперсия от этого не изменится. 2. Если все значения признака уменьшить или увеличить в одно и то же число раз , то дисперсия соответственно уменьшится или увеличится в раз. Среднее квадратическое отклонение равно корню квадратному из дисперсии: S x2 Графическое представление вариационного ряда Графическое изображение зависимости между величинами дает возможность представить эту зависимость наглядно. Графики могут служить основой для открытия новых свойств, соотношений и закономерностей. Наиболее употребительными графиками для изображения вариационных рядов, т. е. соотношений между значениями признака и соответствующими частотами или относительными частотами, являются полигон, гистограмма и кумулята. Полигон чаще всего используют для изображения дискретных рядов. Для построения полигона в прямоугольной системе координат на оси абсцисс в произвольно выбранном масштабе откладывают значения аргумента, т. е. варианты, а на оси ординат также в произвольно выбранном масштабе - значения частот или относительных частот. Масштаб выбирают такой, чтобы была обеспечена необходимая наглядность, и чтобы рисунок имел желательный размер. Далее в этой системе координат строят точки, координатами которых являются пары соответствующих чисел из вариационного ряда. Полученные точки последовательно соединяют отрезками прямой. Крайнюю "левую" точку соединяют с точкой оси абсцисс, абсцисса которой находится слева от рассматриваемой точки на таком же расстоянии, как абсцисса ближайшей справа точки. Аналогично крайнюю "правую" точку также соединяют с точкой оси абсцисс. 20 Пример Количество баллов x 1 2 3 4 5 6 7 8 9 10 11 12 Число учащихся n 1 1 2 3 4 4 6 5 3 3 2 1 Построить полигон частот. Решение. Строим точки основываясь на данных из таблицы. Полученные точки соединяем отрезками прямой. Обратите внимание на точки (0; 0) и (13; 0), расположенные на оси абсцисс и имеющие своими абсциссами числа, на 1 меньшее и большее, чем соответственно абсциссы самой левой и самой правой точек. Полигон частот изображен на рисунке. Если полигон строят по данным интервального ряда, то в качестве абсцисс точек берут середины соответствующих интервалов. Крайние левую и правую точки соединяют с точками оси абсцисс - серединами ближайших интервалов, частоты которых равны нулю. Конечно, в этом случае полигон лишь приближенно отображает зависимость частот от значений аргумента. Кумулята служит для графического изображения кумулятивного вариационного ряда. Для ее построения на оси абсцисс откладывают значения аргумента, а на оси ординат - накопленные частоты или накопленные относительные частоты. Масштаб на каждой оси выбирают произвольно. Далее строят точки, абсциссы которых равны вариантам (в случае дискретных рядов) или верхним границам интервалов (в случае интервальных рядов), а ординаты - соответствующим частотам (накопленным частотам). Эти точки соединяют отрезками прямой. Полученная ломаная и является кумулятой. По данным таблицы составить кумулятивный вариационный ряд, для которого построить кумуляту. 21 Количество баллов x 1 2 3 4 5 6 7 8 9 10 11 12 Число учащихся n 1 1 2 3 4 4 6 5 3 3 2 1 Решение. Cоставим кумулятивный вариационный ряд (см. таблицу ниже), для которого построим кумуляту. Количество баллов 1 2 3 4 5 6 7 8 9 10 11 12 Частота 1 1 2 3 4 4 6 5 3 3 Накопленная частота n 1 2 4 7 11 15 21 26 29 32 34 35 2 1 Гистограмму используют для изображения интервальных рядов. Для построения гистограммы по данным вариационного ряда с равными интервалами, как и для построения полигона, на оси абсцисс откладывают значения аргумента, а на оси ординат - значения частот или относительных частот. Далее строят прямоугольники, основаниями которых служат отрезки оси абсцисс, длины которых равны длинам интервалов, а высотами - отрезки, длины которых пропорциональны частотам или относительным частотам соответствующих интервалов. В результате получают ступенчатую фигуру в виде сдвинутых друг к другу прямоугольников, площади которых пропорциональны частотам (или относительным частотам). Если интервалы неравные, то на оси ординат следует откладывать в произвольно выбранном масштабе значения плотности распределения (абсолютной или относительной). Таким образом, высоты прямоугольников, которые мы строим, должны равняться плотностям соответствующих интервалов. При графическом изображении вариационного ряда с помощью гистограммы плотность изображается так, как если бы она оставалась постоянной внутри каждого интервала. На самом деле, как правило, это не так. Если построить распределение по частям интервалов, то можно убедиться в том, что плотность распределения на различных участках интервала не остается постоянной. Плотность, полученная ранее, предствляла лишь 22 некоторую среднюю плотность. Итак, гистограмма изображает не фактическое изменение плотности распределения, а лишь средние плотности распределения на каждом интервале. Если построена гистограмма интервального распределения, то полигон того же распределения можно получить, если соединить прямолинейными отрезками середины верхних оснований прямоугольников По результатам тестирования по математике учащихся 7-го класса получены данные о доступности заданий теста (отношение числа учащихся, правильно выполнивших задания, к числу тестировавшихся учащихся), предствленные ниже, в таблице. Тест содержал 25 заданий. Построить гистограмму. Доступность задания x, % 25-35 35-45 45-55 55-65 65-75 75-85 85-95 Количество задач n 1 1 5 7 7 3 1 Решение. Откладываем на оси абсцисс 7 отрезков длиной 10. На них, как на основаниях, строим прямоугольники, высоты которых соответственно равны 1, 1, 5, 7, 7, 3, 1. Полученная ступенчатая фигура и является искомой гистограммой. Данные, приведенные в предыдущем примере представим более подробно (см. таблицу ниже.). Построить гистограмму. Доступность задания x, % Количество задач n Доступность задания x, % 30-35 35-40 40-45 45-50 50-55 55-60 1 1 0 3 2 2 60-65 65-70 70-75 75-80 80-85 85-90 23 Количество задач n 5 3 4 0 3 1 Решение. Далее на рисунке построена гистограмма по этим данным. Получено изображение более подробной информации о распределении данных. 24