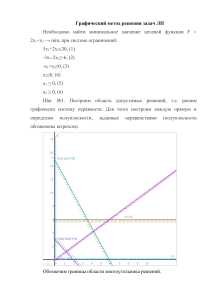
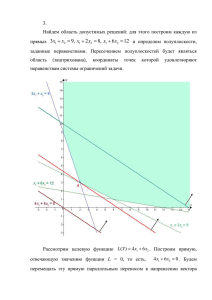
Решение матричной игры
реклама

Решение матричной игры Игроки B1 B2 B3 a = min(Ai) A1 2 -3 2 -3 A2 4 6 -5 -5 A3 -4 5 2 -4 A4 2 3 -1 -1 b = max(Bi) 4 6 2 Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(ai) = -1, которая указывает на максимальную чистую стратегию A4. Верхняя цена игры b = min(bj) = 2. Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах -1 <= y <= 2. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии) В матрице присутствуют отрицательные элементы. Для упрощения расчетов добавим к элементам матрицы (5). Такая замена не изменит решения игры, изменится только ее цена (по теореме фон Неймана). 7 2 7 9 11 0 1 10 7 7 8 4 Математические модели пары двойственных задач линейного программирования можно записать так: найти минимум функции F(x) при ограничениях: 7x1+9x2+x3+7x4 ≥ 1 2x1+11x2+10x3+8x4 ≥ 1 7x1+7x3+4x4 ≥ 1 F(x) = x1+x2+x3+x4 = min найти максимум функции Ф(y) при ограничениях: 7y1+2y2+7y3 ≤ 1 9y1+11y2 ≤ 1 y1+10y2+7y3 ≤ 1 7y1+8y2+4y3 ≤ 1 Ф(y) = y1+y2+y3 = max Решаем эти системы симплексным методом Оптимальный план можно записать так: x1 = 1/19; x3 = 3/38; x2 = 3/76; F(X) = 1•1/19 + 1•3/38 + 1•3/76 = 13/76 Оптимальный план двойственной задачи равен:y1 = 11/152; y2 = 0; y3 = 5/152; y4 = 5/76; ; Z(Y) = 13/76 Цена игры: g = 1 : 13/76 = 76/13 p1=11/26 p2=0/13 p3=5/26 p4=5/13 q1=4/13 q2=3/13 q3=6/13 Поскольку ранее к элементам матрицы было прибавлено число (5), то вычтем это число из цены игры. Цена игры: 11/13 Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Определим минимальное значение целевой функции F(X) = x1 + x2 + x3 + x4 при следующих условиях-ограничений. 7x1 + 9x2 + x3 + 7x4≥1 2x1 + 11x2 + 10x3 + 8x4≥1 7x1 + 7x3 + 4x4≥1 Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≥) вводим базисную переменную x5 со знаком минус. В 2-м неравенстве смысла (≥) вводим базисную переменную x6 со знаком минус. В 3-м неравенстве смысла (≥) вводим базисную переменную x7 со знаком минус. 7x1 + 9x2 + 1x3 + 7x4-1x5 + 0x6 + 0x7 = 1 2x1 + 11x2 + 10x3 + 8x4 + 0x5-1x6 + 0x7 = 1 7x1 + 0x2 + 7x3 + 4x4 + 0x5 + 0x6-1x7 = 1 Умножим все строки на (-1) и будем искать первоначальный опорный план. -7x1-9x2-1x3-7x4 + 1x5 + 0x6 + 0x7 = -1 -2x1-11x2-10x3-8x4 + 0x5 + 1x6 + 0x7 = -1 -7x1 + 0x2-7x3-4x4 + 0x5 + 0x6 + 1x7 = -1 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: -7 -9 -1 -7 1 0 0 -2 -11 -10 -8 0 1 0 -7 0 -7 -4 0 0 1 Базисные переменные это переменные, которые входят только в одно уравнение системы ограничений и притом с единичным коэффициентом. Решим систему уравнений относительно базисных переменных: x5, x6, x7, Полагая, что свободные переменные равны 0, получим первый опорный план: X1 = (0,0,0,0,-1,-1,-1) Базисное решение называется допустимым, если оно неотрицательно. Базис x5 x6 x7 F(X0) B -1 -1 -1 0 x1 -7 -2 -7 1 x2 -9 -11 0 1 x3 -1 -10 -7 1 x4 -7 -8 -4 1 x5 1 0 0 0 x6 0 1 0 0 x7 0 0 1 0 1. Проверка критерия оптимальности. План 0 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец. 2. Определение новой свободной переменной. Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 1-ая строка, а переменную x5 следует вывести из базиса. 3. Определение новой базисной переменной. Минимальное значение θ соответствует 1-му столбцу, т.е. переменную x1 необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-7). Базис x5 x6 x7 F(X0) θ B x1 x2 x3 x4 -1 -9 -1 -7 -7 -1 -2 -11 -10 -8 -1 -7 0 -7 -4 0 1 1 1 1 0 1 : (-7) = -1/7 1 : (-9) = -1/9 1 : (-1) = -1 1 : (-7) = -1/7 x5 1 0 0 0 - x6 0 1 0 0 - x7 0 0 1 0 - 4. Пересчет симплекс-таблицы. Выполняем преобразования симплексной таблицы методом Жордано-Гаусса. Базис x1 x6 x7 F(X0) B 1 /7 -5 /7 0 -1 /7 x1 1 0 0 0 x2 x3 x4 x5 12/7 1/7 1 -1/7 -83/7 -95/7 -6 -2/7 9 -6 3 -1 -2 /7 6/7 0 1/7 x6 0 1 0 0 x7 0 0 1 0 Представим расчет каждого элемента в виде таблицы: B x1 x2 x3 x4 -1 : -7 -7 : -7 -9 : -7 -1 : -7 -7 : -7 -1-(-1 • - -2-(-7 • - -11-(-9 • - -10-(-1 • - -8-(-7 • 2):-7 2):-7 2):-7 2):-7 2):-7 -1-(-1 • - -7-(-7 • - 0-(-9 • - -7-(-1 • - -4-(-7 • 7):-7 7):-7 7):-7 7):-7 7):-7 0-(-1 • 1-(-7 • 1-(-9 • 1):- 1-(-1 • 1):- 1-(-7 • 1):-7 1):-7 7 7 1):-7 x5 1 : -7 0-(1 • 2):-7 0-(1 • 7):-7 0-(1 • 1):-7 x6 0 : -7 1-(0 • 2):-7 0-(0 • 7):-7 0-(0 • 1):-7 x7 0 : -7 0-(0 • 2):-7 1-(0 • 7):-7 0-(0 • 1):-7 1. Проверка критерия оптимальности. План 1 в симплексной таблице является псевдопланом, поэтому определяем ведущие строку и столбец. 2. Определение новой свободной переменной. Среди отрицательных значений базисных переменных выбираем наибольший по модулю. Ведущей будет 2-ая строка, а переменную x6 следует вывести из базиса. 3. Определение новой базисной переменной. Минимальное значение θ соответствует 5-му столбцу, т.е. переменную x5 необходимо ввести в базис. На пересечении ведущих строки и столбца находится разрешающий элемент (РЭ), равный (-2/7). Базис x1 x6 x7 F(X0) θ B 1 /7 -5 /7 0 -1 /7 0 x1 x2 x3 x4 x5 1 -1 1 12/7 /7 1 /7 0 -83/7 -95/7 -6 0 9 -6 3 -1 -2 6 0 /7 /7 0 - -2/7 : (-83/7) = 2/59 6/7 : (-95/7) = -3/34 0 : (-6) = 0 1/7 : (-2/7) = -1/2 x6 0 1 0 0 - x7 0 0 1 0 - 4. Пересчет симплекс-таблицы. Выполняем преобразования симплексной таблицы методом Жордано-Гаусса. Базис x1 x5 x7 F(X1) B 1 /2 21/2 21/2 -1 /2 x1 1 0 0 0 x2 51/2 291/2 381/2 -41/2 x3 5 34 28 -4 x4 4 21 24 -3 x5 x6 x7 0 -1/2 0 1 -31/2 0 0 -31/2 1 0 1/2 0 Представим расчет каждого элемента в виде таблицы: B x1 x2 x3 1 /7-(-5/7 • - 1-(0 • - 12/7-(-83/7 • - 1/7-(-95/7 • 1 1 1 /7):-2/7 1/7):-2/7 /7):-2/7 /7):-2/7 -5 /7 : -2/7 0 : -2/7 -83/7 : -2/7 -95/7 : -2/7 0-(-5/7 • - 0-(0 • - 9-(-83/7 • - -6-(-95/7 • 1):-2/7 1):-2/7 1):-2/7 1):-2/7 -1 6 /7-(0-(0 /7-(-2 / -(7 5 1 1 5 /7 • /7): • /7): 9 /7 • 1/7):3 1 -2 8 / • / ): / 7 7 7 2 2 2 /7 /7 /7 x4 x5 x6 x7 1-(-6 • - -1/7-(-2/7 • - 0-(1 • - 0-(0 • 1 1 1 /7):-2/7 /7):-2/7 /7):-2/7 1/7):-2/7 -6 : -2/7 -2/7 : -2/7 1 : -2/7 0 : -2/7 3-(-6 • - -1-(-2/7 • - 0-(1 • - 1-(0 • 1):-2/7 1):-2/7 1):-2/7 1):-2/7 0-(1 0-(0 1 0-(-6 /7-(1 • /7): • 1/7):• 1/7):-2/7 2/7 • 1/7):-2/7 2 2 /7 /7 В базисном столбце все элементы положительные. Переходим к основному алгоритму симплекс-метода. Итерация №0. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x2, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai2 и из них выберем наименьшее: min (1/2 : 51/2 , 21/2 : 291/2 , 21/2 : 381/2 ) = 5/77 Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (381/2) и находится на пересечении ведущего столбца и ведущей строки. Базис x1 x5 x7 F(X1) B 1 /2 21/2 21/2 -1 /2 x1 x2 x3 x4 x5 x6 x7 1 51/2 5 4 0 -1/2 0 0 291/2 34 21 1 -31/2 0 0 28 24 0 -31/2 1 0 -4 -3 0 1/2 0 min 1 /11 5 /59 0 4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x7 в план 1 войдет переменная x2. Строка, соответствующая переменной x2 в плане 1, получена в результате деления всех элементов строки x7 плана 0 на разрешающий элемент РЭ=381/2 На месте разрешающего элемента в плане 1 получаем 1. В остальных клетках столбца x2 плана 1 записываем нули. Таким образом, в новом плане 1 заполнены строка x2 и столбец x2. Все остальные элементы нового плана 1, включая элементы индексной строки, определяются по правилу прямоугольника. Для этого выбираем из старого плана четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ. НЭ = СЭ - (А*В)/РЭ СТЭ - элемент старого плана, РЭ - разрешающий элемент (381/2), А и В элементы старого плана, образующие прямоугольник с элементами СТЭ и РЭ. Представим расчет каждого элемента в виде таблицы: B x1 x2 51/21 /2-(21/2 • 1-(0 • (381/2 • 51/2):381/2 51/2):381/2 1 5 /2):381/2 21/2291/20-(0 • 1 (21/2 • 1 1 (38 /2 • 29 / ):38 2 291/2):381 291/2):381 /2 /2 /2 1 2 /2 : 381/2 : 1 0 : 38 /2 381/2 381/2 x3 x4 5-(28 • 4-(24 • 1 1 5 /2):38 /2 5 /2):381/2 1 34-(28 • 21-(24 • 291/2):381 291/2):381 /2 /2 28 : 381/2 24 : 381/2 x5 x6 x7 -1 /2-(0-(0 • 0-(1 • 31/2 • 1 1 1 5 /2):38 /2 1 5 / ):381/2 5 /2):381/2 2 -31/2-(1-(0 • 0-(1 • 31/2 • 1 1 29 /2):38 291/2):381 291/2):381 /2 /2 /2 -31/2 : 1 0 : 38 /2 1 : 381/2 381/2 1 /2-(21/2 • -41/2/2-(-31/2 • 0-(0 • -4-(28 • -3-(24 • 0-(0 • 0-(1 • (381/2 • - 1 1 1 1 1 1 1 1 1 4 / ):38 /2 1 4 / ):38 /2 4 /2):38 /2 4 /2):38 /2 1 4 / ):381/2 41/2):381/2 2 4 /2):381/2 2 4 /2):381/2 2 -1 Получаем новую симплекс-таблицу: Базис B 1 x1 /7 x5 45/77 x2 5/77 F(X1) -16/77 x1 1 0 0 0 x2 x3 x4 4 0 1 /7 0 126/11 247/77 1 8/11 48/77 0 -8/11 -15/77 x5 0 1 0 0 x6 x7 0 -1/7 -9 /11 -59/77 -1 /11 2/77 1 /11 9/77 Итерация №1. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai3 и из них выберем наименьшее: min (1/7 : 1 , 45/77 : 126/11 , 5/77 : 8/11 ) = 15/322 Следовательно, 2-ая строка является ведущей. Разрешающий элемент равен (126/11) и находится на пересечении ведущего столбца и ведущей строки. Базис B 1 x1 /7 45 x5 /77 5 x2 /77 -16 F(X2) /77 x1 1 0 0 0 x2 x 3 x4 0 1 4/7 0 247/77 1 8/11 48/77 -15 0 /77 x5 0 1 0 0 x6 x7 0 -1/7 -9 /11 -59/77 -1 /11 2/77 1 /11 9/77 min 1 /7 5 /56 0 4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x5 в план 2 войдет переменная x3. Строка, соответствующая переменной x3 в плане 2, получена в результате деления всех элементов строки x5 плана 1 на разрешающий элемент РЭ=126/11 На месте разрешающего элемента в плане 2 получаем 1. В остальных клетках столбца x3 плана 2 записываем нули. Таким образом, в новом плане 2 заполнены строка x3 и столбец x3. Все остальные элементы нового плана 2, включая элементы индексной строки, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы: B x1 x2 x3 1-(0 • 0-(0 • 1 /7-(45/77 • 1-(126/11 • 6 6 1):12 / 1):12 / 1 1 1):126/11 1):126/11 1 1 x4 x5 x6 0-(1 • 4 /7-(247/77 • 0-(-9/11 • 6 1):12 / 1 1):126/11 1):126/11 1 x7 /7-(-59/77 • 1):126/11 -1 45 -9 -59 /77 : 0: 0: 126/11 : 247/77 : 1: /11 : /77 : 6 6 6 6 6 6 6 12 /11 12 /11 12 /11 12 /11 12 /11 12 /11 12 /11 126/11 5 8 48 -1 2 /770-(0 1-(0 /11/770-(1 /11-(/77-((45/77 • 8/11) • 8/11):1 • 8/11):1 (126/11 • 8/11 (247/77 • 8/11) • 8/11):1 9/11 •8/11): 59/77 • 8/11): :126/11 26/11 26/11 ):126/11 :126/11 26/11 126/11 126/11 1 / -(-16 -8 -15 9 /770-(0 • - 0-(0 • /11/770-(1 • - 9 11 /77-(/ • 11 59 (45/77 • - 8/11):12 8/11):12 (126/11 • (247/77 • - 8/11):12 8 /77 • 6 / ):12 / 11 1 8 6 8 6 8 /11):126/11 6/11 /11 /11):126/11 8/11):126/11 /11 /11):126/11 1 Получаем новую симплекс-таблицу: Базис x1 x3 x2 F(X2) B 31 /322 15 /322 5 /161 -4 /23 x1 1 0 0 0 x2 0 0 1 0 x3 0 1 0 0 x4 x5 117 /322 -11/138 67 /322 11/138 76 /161 -4/69 -1 /23 4/69 x6 x7 3 /46 -79/966 -3 /46 -59/966 -1 /23 34/483 1 /23 5/69 Итерация №2. 1. Проверка критерия оптимальности. Текущий опорный план неоптимален, так как в индексной строке находятся отрицательные коэффициенты. 2. Определение новой базисной переменной. В качестве ведущего выберем столбец, соответствующий переменной x4, так как это наибольший коэффициент по модулю. 3. Определение новой свободной переменной. Вычислим значения Di по строкам как частное от деления: bi / ai4 и из них выберем наименьшее: min (31/322 : 117/322 , 15/322 : 67/322 , 5/161 : 76/161 ) = 5/76 Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (76/161) и находится на пересечении ведущего столбца и ведущей строки. Базис B x1 x2 x3 x1 31/322 1 0 0 x4 x5 x6 117 /322 -11/138 3/46 x7 min -79 /966 31/117 x3 15/322 0 0 1 x2 5/161 0 1 0 F(X3) -4/23 0 0 0 67 /322 11 /138 -3/46 -4 /69 -1/23 4 /69 1/23 -59 /966 34 /483 5 /69 15 /67 0 4. Пересчет симплекс-таблицы. Формируем следующую часть симплексной таблицы. Вместо переменной x2 в план 3 войдет переменная x4. Строка, соответствующая переменной x4 в плане 3, получена в результате деления всех элементов строки x2 плана 2 на разрешающий элемент РЭ=76/161 На месте разрешающего элемента в плане 3 получаем 1. В остальных клетках столбца x4 плана 3 записываем нули. Таким образом, в новом плане 3 заполнены строка x4 и столбец x4. Все остальные элементы нового плана 3, включая элементы индексной строки, определяются по правилу прямоугольника. Представим расчет каждого элемента в виде таблицы: B x1 x2 x3 x4 x5 x6 x7 31 117 -11 3 -79 /3221-(0 0-(1 0-(0 /322/138-(/46-(/9665 117 117 117 117 76 117 4 117 1 117 34 ( /161 • /32 • /322) • /322) • /322) ( /161 • /3 /69 • /322 /23 • /322 ( /483 •117/3 76 76 76 :76/161 :76/161 :76/161 ):76/161 ):76/161 2): /161 22): /161 22): /161 15 67 11 -3 -59 /3220-(0 0-(1 1-(0 /322/138-(/46-(/9665 67 67 67 67 76 67 4 67 1 67 34 ( /161 • /322 • /322): • /322): • /322): ( /161 • /32 /69 • /322) /23 • /322) ( /483 •67/32 76 76 76 76 76 ):76/161 /161 /161 /161 :76/161 :76/161 2): /161 2): /161 5 /161 : 76/161 0 : 76/161 1 : 76/161 0 : 76/161 /230-(0 • - 0-(1 • - 0-(0 • 1 ( /161 • /23):76/1 1/23):76/1 1/23):76/1 1 /23):76/161 61 61 61 -4 5 76 /161 : 76/161 -1 /23( /161 • 1 /23):76/161 76 4 - /69 : 76/161 1/23 : 76/161 4 1 /69-(/23-(4 1 /69 • /23 • 1 /23):76/161 1/23):76/161 34 /483 : 76/161 5 /69( /483 • 1 /23):76/161 34 Получаем новую симплекс-таблицу: Базис x1 x3 x4 F(X3) B 11 /152 5 /152 5 /76 -13 /76 x1 x2 1 -117/152 0 -67/152 0 29/76 0 7/76 x3 0 1 0 0 x4 0 0 1 0 x5 x6 x7 -2 /57 15/152 -31/228 2 /19 -7/152 -7/76 -7 /57 -7/76 17/114 1 /19 3/76 3/38 1. Проверка критерия оптимальности. Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи. Окончательный вариант симплекс-таблицы: Базис x1 x3 x4 F(X4) B 11 /152 5 /152 5 /76 -13 /76 x1 x2 1 -117/152 0 -67/152 0 29/76 0 7/76 x3 0 1 0 0 x4 0 0 1 0 x5 x6 x7 -2 /57 15/152 -31/228 2 /19 -7/152 -7/76 -7 /57 -7/76 17/114 1 /19 3/76 3/38 Оптимальный план можно записать так: x1 = 11/152 x3 = 5/152 x4 = 5/76 F(X) = 1•11/152 + 1•5/152 + 1•5/76 = 13/76 Анализ оптимального плана. Значение 0 в столбце x1 означает, что использование x1 - выгодно. Значение 7/76> 0 в столбце x2 означает, что использование x2 - не выгодно. Значение 0 в столбце x3 означает, что использование x3 - выгодно. Значение 0 в столбце x4 означает, что использование x4 - выгодно. Значение 1/19 в столбце x5 означает, что теневая цена (двойственная оценка) равна 1/19. Значение 3/76 в столбце x6 означает, что теневая цена (двойственная оценка) равна 3/76. Значение 3/38 в столбце x7 означает, что теневая цена (двойственная оценка) равна 3/38. Ответы на вопросы преподавателя: 1. По какому методу пересчитываются симплекс-таблицы? Используется правило прямоугольника (метод жордановских преобразований). 2. Обязательно ли каждый раз выбирать максимальное значение из индексной строки? Можно не выбирать, но это может привести к зацикливанию алгоритма. 3. В индексной строке в n-ом столбце нулевое значение. Что это означает? Нулевые значения должны соответствовать переменным, вошедшим в базис. Если в индексной строке симплексной таблицы оптимального плана находится нуль, принадлежащий свободной переменной, не вошедшей в базис, а в столбце, содержащем этот нуль, имеется хотя бы один положительный элемент, то задача имеет множество оптимальных планов. Свободную переменную, соответствующую указанному столбцу, можно внести в базис, выполнив соответствующие этапы алгоритма. В результате будет получен второй оптимальный план с другим набором базисных переменных. Составим двойственную задачу к прямой задаче. 7y1 + 2y2 + 7y3≤1 9y1 + 11y2≤1 y1 + 10y2 + 7y3≤1 7y1 + 8y2 + 4y3≤1 y1 + y2 + y3 → max y1 ≥ 0 y2 ≥ 0 y3 ≥ 0 Решение двойственной задачи дает оптимальную систему оценок ресурсов. Используя последнюю итерацию прямой задачи найдем, оптимальный план двойственной задачи. Из теоремы двойственности следует, что Y = C*A-1. Составим матрицу A из компонентов векторов, входящих в оптимальный базис. 71 7 A = (A1, A3, A4) = 2 10 8 77 4 Определив обратную матрицу D = А-1 через алгебраические дополнения, получим: 2/57 -15/152 31/228 -1 D = A = -2/19 7/152 7/57 7/76 7/76 -17/114 Как видно из последнего плана симплексной таблицы, обратная матрица A1 расположена в столбцах дополнительных переменных. Тогда Y = C*A-1 = 2/57 -15/152 31/228 (1, 1, 1) x -2/19 7/152 7/57 7/76 7/76 = (1/19;3/76;3/38) -17/114 Оптимальный план двойственной задачи равен: y1 = 1/19 y2 = 3/76 y3 = 3/38 Z(Y) = 1*1/19+1*3/76+1*3/38 = 13/76 Критерий оптимальности полученного решения. Если существуют такие допустимые решения X и Y прямой и двойственной задач, для которых выполняется равенство целевых функций F(x) = Z(y), то эти решения X и Y являются оптимальными решениями прямой и двойственной задач соответственно. Определение дефицитных и недефицитных (избыточных) ресурсов. Вторая теорема двойственности. Подставим оптимальный план прямой задачи в систему ограниченной математической модели: 7*11/152 + 9*0 + 1*5/152 + 7*5/76 = 1 = 1 2*11/152 + 11*0 + 10*5/152 + 8*5/76 = 1 = 1 7*11/152 + 0*0 + 7*5/152 + 4*5/76 = 1 = 1 1-ое ограничение прямой задачи выполняется как равенство. Это означает, что 1-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y1>0). 2-ое ограничение прямой задачи выполняется как равенство. Это означает, что 2-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y2>0). 3-ое ограничение прямой задачи выполняется как равенство. Это означает, что 3-ый ресурс полностью используется в оптимальном плане, является дефицитным и его оценка согласно второй теореме двойственности отлична от нуля (y3>0). Таким образом, отличную от нуля двойственные оценки имеют лишь те виды ресурсов, которые полностью используются в оптимальном плане. Поэтому двойственные оценки определяют дефицитность ресурсов. Обоснование эффективности оптимального плана. При подстановке оптимальных двойственных оценок в систему ограничений двойственной задачи получим: 7*1/19 + 2*3/76 + 7*3/38 = 1 = 1 9*1/19 + 11*3/76 + 0*3/38 = 69/76 < 1 1*1/19 + 10*3/76 + 7*3/38 = 1 = 1 7*1/19 + 8*3/76 + 4*3/38 = 1 = 1 Анализ устойчивости оптимального плана. Проведем анализ устойчивости оптимального плана и оценим степень влияния изменения ресурсов на значение целевой функции. Чувствительность решения к изменению коэффициентов целевой функции. Так как любые изменения коэффициентов целевой функции оказывают влияние на оптимальность полученного ранее решения, то наша цель - найти такие диапазоны изменения коэффициентов в целевой функции (рассматривая каждый из коэффициентов отдельно), при которых оптимальные значения переменных остаются неизменными. Пусть каждое значение параметра целевой функции изменится на ∆ сi. Найдем интервалы, при которых будет экономически выгодно использование ресурсов. Допустимые диапазоны изменения коэффициентов в целевой функции определятся из соотношений: 1-ый параметр целевой функции может изменяться в пределах: ∆c-1 = min [yk/d1k] для d1k>0. ∆c+1 = |max[yk/d1k]| для d1k<0. где в знаменателе коэффициенты столбцов свободных переменных в оптимальном плане (коэффициенты структурных сдвигов, элементы обратной матрицы к базису оптимального плана). Таким образом, 1-параметр может быть уменьшен на 18/31 или увеличен на 2/5 Интервал изменения равен: (c1 - ∆c1-; c1 + ∆c1+) [1-18/31; 1+2/5] = [13/31;7/5] Если значение c1 будет лежать в данном интервале, то оптимальный план не изменится. 3-ый параметр целевой функции может изменяться в пределах: ∆c-3 = min [yk/d3k] для d3k>0. ∆c+3 = |max[yk/d3k]| для d3k<0. Таким образом, 3-параметр может быть уменьшен на 6/7 или увеличен на 1/2 Интервал изменения равен: (c3 - ∆c3-; c3 + ∆c3+) [1-6/7; 1+1/2] = [1/7;3/2] Если значение c3 будет лежать в данном интервале, то оптимальный план не изменится. 4-ый параметр целевой функции может изменяться в пределах: ∆c-4 = min [yk/d4k] для d4k>0. ∆c+4 = |max[yk/d4k]| для d4k<0. Таким образом, 4-параметр может быть уменьшен на 3/7 или увеличен на 9/17 Интервал изменения равен: (c4 - ∆c4-; c4 + ∆c4+) [1-3/7; 1+9/17] = [4/7;26/17] Если значение c4 будет лежать в данном интервале, то оптимальный план не изменится. Чувствительность решения к изменению запасов сырья. Из теоремы об оценках известно, что колебание величины bi приводит к увеличению или уменьшению f(X). Оно определяется величиной yi в случае, когда при изменении величин bi значения переменных уi в оптимальном плане соответствующей двойственной задачи остаются неизменными. Поэтому необходимо найти такие интервалы изменения каждого из свободных членов системы ограничений исходной ЗЛП, в которых оптимальный план двойственной задачи не менялся бы. Найдем интервалы устойчивости ресурсов. 1-ый запас может изменяться в пределах: ∆b-1 = min[xk/dk1] для dk1>0. ∆b+1 = |max[xk/dk1]| для dk1<0. Таким образом, 1-ый запас может быть уменьшен на 15/28 или увеличен на 5/16 Интервал изменения равен: (b1 - ∆b-1; b1 + ∆b+1) [1-15/28; 1+5/16] = [13/28;21/16] 2-ый запас может изменяться в пределах: ∆b-2 = min[xk/dk2] для dk2>0. ∆b+2 = |max[xk/dk2]| для dk2<0. Таким образом, 2-ый запас может быть уменьшен на 5/7 или увеличен на 11/15 Интервал изменения равен: (b2 - ∆b-2; b2 + ∆b+2) [1-5/7; 1+11/15] = [2/7;26/15] 3-ый запас может изменяться в пределах: ∆b-3 = min[xk/dk3] для dk3>0. ∆b+3 = |max[xk/dk3]| для dk3<0. Таким образом, 3-ый запас может быть уменьшен на 5/14 или увеличен на 15/34 Интервал изменения равен: (b3 - ∆b-3; b3 + ∆b+3) [1-5/14; 1+15/34] = [9/14;49/34] 1-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 1-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x1>0). 2-ое ограничение выполняется как строгое неравенство, т.е. ресурс 2-го вида использовать экономически не выгодно. И действительно в оптимальном плане прямой задачи x2 = 0. Поскольку теневая (альтернативная) цена меньше рыночной цены этого продукта, то производство данного продукта выгодно. При этом разница между ценами (69/76 - 1 = -7/76) показывает величину изменения целевой функции F(x) при введении дополнительной единицы xi. 3-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 3-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x3>0). 4-ое ограничение двойственной задачи выполняется как равенство. Это означает, что 4-ый ресурс экономически выгодно использовать, а его использование предусмотрено оптимальным планом прямой задачи (x4>0). Влияние запасов ресурсов на оптимальное решение прямой задачи. Величина двойственной оценки показывает, на сколько уменьшается значение целевой функции F(x) при уменьшении дефицитного ресурса на единицу. -1 2 3 A = 2 1 -4 2 31 BT = (1,1,1) Главный определитель: