Лабораторная работа № 6. Общая задача линейного программирования. Двойственность в задачах

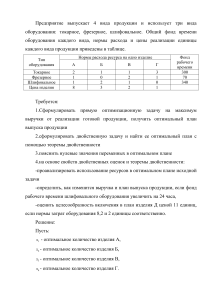
Лабораторная работа № 6.
Общая задача линейного программирования. Двойственность в задачах
линейного программирования. Анализ решения задач линейного
программирования.
Цель работы:
1) ознакомиться с теорией двойственности;
2) научиться применять теорию двойственности к решению задач ЛП и
анализировать полученные результаты.
Теоретические сведения
Каждой задаче линейной оптимизации можно поставить в соответствие
задачу, называемую двойственной к ней.
Пусть дана общая задача линейной оптимизации (исходная задача):
x j произвольного знака при j  n1  1, n .
Двойственная к ней задача имеет вид:
u i произвольного знака при i  m1  1, m .
Двойственная задача строится по следующим правилам:
1) упорядочивается запись исходной задачи, т.е. если целевая функция задачи
максимизируется, то ограничения неравенства должны быть вида  , если
минимизируется — то вида . Выполнение этих условий достигается умножением
соответствующих ограничений на (-1);
2) если исходная задача является задачей максимизации, то двойственная
будет задачей минимизации. При этом вектор, образованный из коэффициентов при
неизвестных целевой функции исходной задачи, совпадает с вектором констант в
правых частях системы ограничений двойственной задачи, и, наоборот,
коэффициентами при неизвестных целевой функции двойственной задачи являются
соответствующие правые части системы ограничений исходной задачи;
3) каждой переменной u i двойственной задачи соответствует i-е ограничение
исходной задачи, и, наоборот, каждой переменной x j прямой задачи соответствует je ограничение двойственной задачи;
4) матрица из коэффициентов при неизвестных двойственной задачи
образуется транспонированием матрицы, составленной из коэффициентов при
неизвестных системы ограничений исходной задачи;
5) если на
j-ю переменную исходной задачи наложено условие
неотрицательности,
то
j-e ограничение двойственной задачи будет неравенством, в противном случае j-e
ограничение будет равенством; аналогично связаны между собой ограничения
исходной задачи и переменные двойственной.
Дадим экономическую интерпретацию пары двойственных задач.
Рассмотрим задачу рационального использования ресурсов. Пусть
предприятие располагает ресурсами b1 , b2 ,, bm , которые могут использоваться для
выпуска п видов продукции. Пусть также известны стоимость единицы j-го вида
продукции c j ( j  1, n) и норма потребления i-го ресурса (i  1, m) на производство
единицы j-й продукции — аij.
Требуется определить объем производства продукции каждого вида x j ( j  1, n) ,
максимизирующий суммарную стоимость
При этом расход ресурсов не должен превышать их наличия:
Все неизвестные по своему экономическому смыслу неотрицательны:
По исходным данным сформулируем другую экономическую задачу
(двойственную).
Предположим, что некоторая организация может закупить все ресурсы,
которыми располагает предприятие. Необходимо определить оптимальные цены
(оценки) ui* (i  1, m) на эти ресурсы исходя из естественного условия, что
покупающая организация стремится минимизировать общую оценку ресурсов.
Нужно, однако, учитывать и тот факт, что за ресурсы покупающая организация
должна уплатить сумму, не меньшую той, которую может выручить предприятие
при организации собственного производства продукции.
Математическая модель задачи имеет вид
Здесь ~f — общая оценка ресурсов. Каждое j-е ограничение из системы
представляет собой неравенство, левая часть которого равна оценке всех ресурсов,
расходуемых на производство единицы j-го вида продукции, а правая — стоимости
единицы этой продукции.
Порядок выполнения работы
1 Ознакомиться с теоретическими сведениями.
2 - Построить двойственную задачу к заданной (прямой) задаче (номер
задачи выбирает преподаватель).
- Решить одну из пары двойственных задач и по найденному решению найти
решение второй задачи.
- Объяснить смысл всех переменных участвующих в решении задачи.
- Указать наиболее дефицитный и избыточный ресурс, если он имеется.
Содержание отчета:
1 Тема и цель работы.
2 Условия задач.
3 Ход решения, результаты.
4 Выводы по работе.
Список задач
№
Составить задачу, двойственную к указанной.
вар.
Z = 2x1 - x2 + x3 -3x4 +x5 max
Z = 7x1 + 6x2 + 3x3 –x4 min
5
 x 1  3x 2  x 3  2x 4
 2x 1  x 2  2x 3  3x 4  12
 2x 1  x 2  2x 3  x 4  x 5  8

I
  x 1  2x 2  x 3  x 4  10
 x  x  3x  x  2x  9
1
2
3
4
5
 3x 1  5x 2

 4x 4  7
  x 1  2x 2  x 3  3x 4  x 5  4
x2,3  0
x1,3  0
Z = 2x1 - x2 + x3 + x4 - 2x5 max
Z = x1 + 2x2 + 3x3 +x4 max
 3x 1  2x 2  x 3  x 4  x 5  8
 x1  x 2  x 3  x 4  4
 x 1  3x 2  x 3  3x 4  2x 5  6
 2x 1  3x 2  4x 3  x 4  2
III
 x x x x
 3x  3x  3x  x  3
5
2
3
4
2
3
4
 1
 1
2
x

5
x

x

3
x

7
x

5
x
6
1
2
4
5
2

 1
x1,2,4  0
x4  0
Z = x1 + x2 + x3 max
Z = x1 + 2x2 + 3x3 +4x4 +5x5 min
x

x

x

x

2
 1
2
3
4
 x1  x 2  x 3  x 4  x 5  0
 2x 1  x 2  x 3  4x 4  0

 x 4 x5  0
V
 10x  9x  9x  10x  8
 x1
1
2
3
4


 x5  1
 x1
 x 1  3x 2  3x 3  x 4  8
x1,2  0; x5  0
x1,2  0
№
вар.
II
IV
VI
VII
IX
XI
Z = x1 - x2 - 2x3 -3x4 min
 x1  x 2  x 3  x 4  1

 x4  5
 x1

x2  x3
 10
x1,2,3  0
Z = 7x1 + 6x2 + 3x3 - x4 max
 2x 1  x 2  2x 3  3x 4  12

  x 1  2x 2  x 3  x 4  10
 3x 1  5x 2
 4x 4  7
x2,3  0





x1,3  0
Z = x2 - x3 +x4 min
3x 1  x 2
2
x 2  3x 3
 1
4x 3  x 4  3
5x 1
 x4  6
L(X)  10 x 1  40 x 3  13x 4  56 x 5  min;
21x 1 9x 2  2x 4  12 x 5  58,

110 x 2  60 x 3  80 x 4  45 x 5  290,

5x 2  27 x 3  14 x 4  x 5  72,
87 x  6,4x  130 x  140,
1
2
4

x j  0 j  1,5 .

7 x  16 x  5x  25x  600,
3
4
5
 1
8
x

1
,
7
x

0
,
5
x

4
,
7 x 5  890,
 1
2
4

6x 1 4x 3  7 x 4  6,3x 5  270,
84 x  62 x  80 x  14 x  2300 ,
1
2
3
5

x j  0 j  1,5 .


L(X)  84 x1  5,7 x 2  10 x 4  3x 5  max;
4x  8,5x  16 x  10 x  50,
2
3
5
 1
10,4x 1  6x 3  2x 4  4x 5  120,
XIII 
19 x 1 18 x 2  20 x 4  30 x 5  600,
200 x  45x  8x  3,4x  210,
1
2
3
4

x j  0 j  1,5 .



L(X)  x1  4 x 3  8x 4  12 x 5  min;
x  9 x  2 x  4 x  250,
2
3
4
 1
0,4 x1  x 2  5x 3  3x 4  8x 5  460,

0,5x1  10x 2 - 8x 3  6 x 4  2 x 5  190,
11x  8,5x  3x  2x  210,
3
4
5
 2
x j  0 j  1,5 .



VIII
X
x1,3  0
L(X)  4x 1  6x 2  14 x 3  49 x 5  min;

XV
Z = x1 - 10x2 + 2x3 - x4 +7x5 max
 x4
1
 2x 1  x 2
 x 1  x 2  2x 3  x 4  x 5  4

x2  x3
0

 x3
 2x 5  3
 x1

XII

L(X)  0,84 x 2  4x 3  3,8x 4  12 x 5  min;
15x 1 9,6x 2  34 x 4  8x 5  180,

0,6x 1 11,1x 2  2,6x 3  1,5x 4  6,3x 5  68,

VX
14 x 1 64 x 3  38 x 4  12 x 5  81,
190 x  148 x  7 x  84 x  230,
1
2
3
5

x j  0 j  1,5 .



L(X)  45x1  65x 2  2 x 4  3x 5  max;
15x 1 18x 2  34x 4  22x 5  56,

2 x1  7 x 3  4 x 4  3x 5  91,
XVI

0,2 x 1 0,8x 2  1,5x 3  0,9 x 4  4 x 5  26,
1,8x  42x  6,4 x  3x  15,
1
2
3
5

x j  0 j  1,5 .


