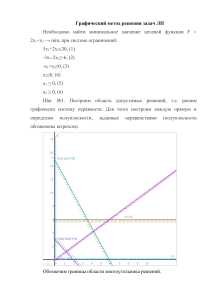
Найдем область допустимых решений: для этого
реклама

3. Найдем область допустимых решений: для этого построим каждую из прямых 3x1 x2 9, x1 2 x2 8, x1 6 x2 12 и определим полуплоскости, заданные неравенствами. Пересечением полуплоскостей будет являться область (заштрихована), координаты точек которой удовлетворяют неравенствам системы ограничений задачи. Рассмотрим целевую функцию L( x ) 4 x1 6 x2 . Построим прямую, отвечающую значению функции L = 0, то есть, 4 x1 6 x2 0 . Будем перемещать эту прямую параллельным переносом в направлении вектора градиента 4;6 для определения минимального значения функции L( x ) до первого касания с областью допустимых решений (на рисунке эта прямая выделена красным цветом), а для определения максимального значения – до последнего касания с областью допустимых решений. В первом случае получаем точку А, как результат пересечения прямых 3x1 x2 9 и x1 2 x2 8 . Во втором случае – такой точки нет, целевая функция не ограничена сверху. Определим координаты точки А, решив систему уравнений 3x1 x2 9, x1 2 x2 8. Получаем А(2; 3). Таким образом, целевая функция принимает минимальное значение при x1 = 2, x2 = 3, ее значение L 4 2 6 3 26. Максимальное значение равно . 17. Приведем задачу к канонической форме. Для этого введем дополнительные переменные x5 , x6 . Получаем 2 x1 x2 4 x3 3x4 x5 0 x6 3, 3x1 x2 2 x3 5 x4 0 x5 x6 1. Решим систему уравнений относительно переменных x5 , x6 . Полагая, что свободные переменные равны 0, найдем первый опорный план x0 = (0, 0, 0, 3, 1). Составим симплекс-таблицу: Базис x5 x6 L( x0 ) B 3 1 0 x1 2 3 -3 x2 1 -1 -1 x3 4 2 -1 x4 3 5 -1 x5 1 0 0 x6 0 1 0 Итерация 0. Текущий опорный план неоптимален, так как в индексной строке есть отрицательные коэффициенты. В качестве ведущего выберем столбец, в котором находится наибольший коэффициент, то есть столбец, соответствующий переменной x1. Вычислим значения частного от деления bi / ai1 и из них выберем наименьшее. Вторая строка является ведущей. Разрешающий элемент находится на пересечении ведущего столбца и ведущей строки и равен 3. Базис B x1 x2 x3 x4 x5 x6 bi / ai1 x5 3 2 1 4 3 1 0 11/2 x6 L( x0 ) 1 3 -1 2 5 0 1 1/ 3 0 -3 -1 -1 -1 0 0 0 Получаем новую симплекс-таблицу: Базис x5 x1 L( x1 ) B 21/3 1 /3 x1 0 1 x2 12/3 -1 /3 x3 22/3 2 /3 x4 /3 2 1 /3 x5 1 0 1 0 -2 1 4 0 -1 x6 /3 1 /3 -2 1 Итерация 1. Текущий опорный план неоптимален, так как в индексной строке есть отрицательные коэффициенты. Аналогично предыдущему определяем разрешающий элемент – он 2 3 находится на пересечении первого столбца и первой строки, и равен 1 . Базис B x5 1 x1 x2 x3 x4 0 12/3 2 -1 /3 1 -1 1 0 -2 2 /3 x1 L( x1 ) 1 x5 x6 /3 1 -2 /3 12/3 0 1 1 4 0 2 /3 2 /3 bi / ai2 /3 12/5 - 1 0 /3 Получаем новую симплекс-таблицу: Базис x2 x1 L( x2 ) B 12/5 4 /5 4 3 /5 x1 0 x2 1 x3 13/5 1 0 0 0 x4 /5 x5 /5 -1 3 11/5 13/5 1 1 3 4 /5 3 /5 x6 /5 -2 /5 1 /5 1 1 /5 1 /5 Индексная строка не содержит отрицательных элементов, значит, найден оптимальный план. 4 2 Оптимальный план: x1 , x2 1 ; максимальное значение целевой 5 5 4 2 4 функции L( x ) 3 1 3 . 5 5 5 22. Пусть x1, x2, x3 – количество партий товаров 1, 2 и 3 вида соответственно. Получаем следующую математическую модель: 5 x1 8 x2 6 x3 max, 0,5 x1 0, 7 x2 0, 6 x3 370, 0,1x1 0,3x2 0, 2 x3 90. Найдем решение полученной задачи симплекс-методом. Умножим неравенства на 10 и приведем задачу к канонической форме. Для этого введем дополнительные переменные x4 , x5 . Получим 5 x1 7 x2 6 x3 x4 0 x5 3700, x1 3x2 2 x3 0 x4 x5 900. Решим систему уравнений относительно переменных x4 , x5 . Полагая, что свободные переменные равны 0, найдем первый опорный план x0 = (0, 0, 0, 3700, 900). Составим симплекс-таблицу: Базис x4 B 3700 x1 5 x2 7 x3 6 x4 1 x5 0 x5 L( x0 ) 900 1 3 2 0 1 0 -5 -8 -6 0 0 Итерация 0. Текущий опорный план неоптимален, так как в индексной строке есть отрицательные коэффициенты. В качестве ведущего выберем столбец, в котором находится наибольший коэффициент, то есть столбец, соответствующий переменной x2. Вычислим значения частного от деления bi / ai2 и из них выберем наименьшее. Вторая строка является ведущей. Разрешающий элемент находится на пересечении ведущего столбца и ведущей строки и равен 3. Базис x4 B 3700 x1 5 x2 7 x3 6 x4 1 x5 0 bi / ai2 x5 L( x0 ) 900 1 3 2 0 1 0 -5 -8 -6 0 0 300 0 5284/7 Получаем новую симплекс-таблицу: Базис x4 B 1600 x2 L( x1 ) 300 x1 22/3 1 x2 0 /3 1 2400 -2 /3 x3 11/3 1 2 0 -2 x4 1 /3 x5 -21/3 1 0 /3 /3 2 0 2 /3 Итерация 1. Текущий опорный план неоптимален, так как в индексной строке есть отрицательные коэффициенты. Аналогично предыдущему определяем разрешающий элемент – он 2 3 находится на пересечении первого столбца и первой строки, и равен 2 . Базис x4 x2 L( x1 ) B 1600 300 x1 22/3 1 /3 2400 -21/ x2 0 3 x3 11/3 1 2 0 -2 x4 1 /3 1 0 /3 bi / ai1 x5 -21/3 600 900 /3 2 0 2 /3 0 Получаем симплекс-таблицу: Базис x1 B 600 x1 1 x2 0 x2 L( x2 ) 100 0 1 1 0 1 3800 0 x3 /2 1 x4 /8 3 /2 -1 /2 7 x5 /8 -7 /8 5 /8 /8 5 /8 Индексная строка не содержит отрицательных элементов, значит, найден оптимальный план. Оптимальный план: x1 600, x2 100; максимальное значение целевой функции L( x ) 5 600 8 100 3800. Таким образом, наибольшую прибыль приносит реализация 600 партий товара 1 вида, 100 партий товара 2 вида и отказ от реализации товара 3 вида. 32. Двум ограничениям исходной задачи поставим в соответствие две двойственные переменные у1, у2. Количество переменных исходной задачи равно количеству ограничений двойственной. Матрицы коэффициентов систем ограничений прямой и двойственной задач являются транспонированными друг к другу. Коэффициенты целевой функции прямой задачи станут свободными членами системы ограничений двойственной задачи. Так как целевая функция прямой задачи исследуется на минимум, то целевая функция двойственной задачи будет исследоваться на максимум. Вид неравенств ограничений выбирается по целевой функции. Свободные члены системы ограничений прямой задачи станут коэффициентами целевой функции двойственной. Получим двойственную задачу: L( y ) 2 y1 6 y2 max, 2 y1 2 y2 1, y1 y2 1, 2 y1 3 y2 6, y1 5 y2 1. Решим исходную задачу методом искусственного базиса. Введем искусственные переменные x5 , x6 ; получим 2 x1 x2 2 x3 x4 x5 0 x6 2, 2 x1 x2 3x3 5 x4 0 x5 x6 6. Целевую функцию запишем в виде L( x ) x1 x2 6 x3 x4 Mx5 Mx6 , где M 1. Выразим из системы уравнений переменные x5 , x6 : x5 2 2 x1 x2 2 x3 x4 , x6 6 2 x1 x2 3x3 5 x4 , и подставим их в целевую функцию. Получим L( x ) x1 x2 (6 5M ) x3 (1 6M ) x4 8M . Полагая, что свободные переменные равны 0, найдем первый опорный план x0 = (0, 0, 0, 0, 2, 6). Составим симплекс-таблицу: Базис x5 B 2 x1 2 x2 -1 x3 2 x4 1 x5 1 x6 0 x6 L( x0 ) 6 -2 1 3 5 0 1 8M 1 -1 -6+5M 1+6M 0 0 Итерация 0. Текущий опорный план неоптимален, так как в индексной строке есть положительные коэффициенты. В качестве ведущего выберем столбец, в котором находится наибольший коэффициент, то есть столбец, соответствующий переменной x4. Вычислим значения частного от деления bi / ai4 и из них выберем наименьшее. Вторая строка является ведущей. Разрешающий элемент находится на пересечении ведущего столбца и ведущей строки и равен 5. Базис x5 x6 L( x0 ) B 2 6 x1 2 -2 x2 -1 1 x3 2 3 x4 1 x6 0 1 bi / ai4 2 5 x5 1 0 8M 1 -1 -6+5M 1+6M 0 0 0 11/5 Получаем новую симплекс-таблицу: Базис x5 x4 L( x1 ) B /5 x1 22/5 4 11/5 1 4 -2 2 x2 -11/5 1 /5 2 1 x3 12/5 3 /5 1 3 /5 2 -1 /5+ /5M 1 /5+2 /5M -1 /5-1 /5M -6 /5+1 /5M x4 0 x5 1 1 0 0 0 x6 /5 -1 1 -1 /5 /5-11/5M Итерация 1. Текущий опорный план неоптимален, так как в индексной строке есть положительные коэффициенты. Аналогично предыдущему определяем разрешающий элемент – он 2 5 находится на пересечении первого столбца и первой строки, и равен 2 . Базис x5 x4 L( x1 ) B /5 x1 22/5 -2 /5 4 11/5 1 x2 -11/5 1 4 1 x3 12/5 3 /5 1 3 /5 2 -1 /5+ /5M 12/5+22/5M -1 /5-1 /5M -6 /5+1 /5M x4 0 x5 1 1 0 0 x6 /5 /5 bi / ai1 1/ 3 - /5-11/5M 0 -1 1 -1 0 Получаем новую симплекс-таблицу: Базис x1 x4 L( x2 ) B /3 x1 1 11/3 0 -12/3 0 1 x2 /2 -1 0 -1 /2 x3 /12 x4 0 5 /6 1 -75/12 0 7 x5 /12 x6 /12 5 1 -7 -1 1 /6 /12-M -1 /6 /12-M Индексная строка не содержит положительных элементов, значит, план является оптимальным. Итак, оптимальный план: 1 1 x1 , x4 1 ; 3 3 1 1 2 минимальное значение целевой функции L( x ) 1 1 . 3 3 3