7163
реклама

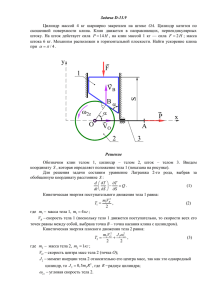
7163. Клин массой М = 0,5 кг с углом при основании α = 30° покоится на гладком горизонтальном столе. На наклонную поверхность клина ставят заводной автомобиль массой m = 0,1 кг и отпускают с нулевой начальной скоростью, после чего автомобиль начинает движение вверх по клину в плоскости рисунка. Найти скорость и автомобиля относительно клина в момент, когда клин приобретает относительно стола скорость v=2 см/с. Дано: М = 0,5 кг; α = 30°; m = 0,1 кг; v=2 см/с. Найти: u=? Решение. При решении задачи пренебрежем влиянием воздуха и будем использовать инерциальную систему отсчета, связанную со столом, который будем считать неподвижным. Свяжем со столом прямоугольную декартову систему координат и направим ее ось ОХ в горизонтальном направлении в плоскости рисунка. В данной инерциальной системе отсчета можно применять закон сохранения импульса автомобиля и клина вдоль оси ОХ, поскольку внешние силы вдоль этого направления отсутствуют (стол по условию горизонтальный и гладкий). Следовательно, в выбранной системе отсчета выполняется соотношение: 𝑚 ∙ 𝑢0𝑥 − 𝑀 ∙ 𝑣 = 0, где v - модуль скорости клина относительно стола, u0x - горизонтальная проекция абсолютной скорости автомобиля и0 на ось ОХ. По закону сложения скоростей (см. рисунок) 𝑢 ⃗0 =𝑣+𝑢 ⃗, где u - скорость автомобиля относительно клина, v - скорость клина относительно стола. В проекции на ось ОХ это равенство имеет вид: 𝑢0𝑥 = 𝑢𝑥 − 𝑣 = 𝑢 ∙ cos 𝛼 − 𝑣. Объединяя записанные соотношения, получаем: 𝑀+𝑚 𝑢= ∙ 𝑣. 𝑚 ∙ cos 𝛼 Подставляя в эту формулу заданные в условии задачи числа и проверяя размерность, находим ответ: 0,5 + 0,1 см см 𝑢= ∙2 = 14 . 0,1 ∙ cos 30° с с Ответ. 𝑴+𝒎 см 𝒖= ∙ 𝒗, 𝒖 = 𝟏𝟒 . 𝒎 ∙ 𝐜𝐨𝐬 𝜶 с