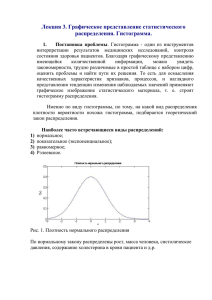
Гистограмма.Анализ распределения
реклама
Графическое представление вариационного ряда. Анализ распределения Анализ каждой произвольной выборки, представляющей собой совокупность независимых, одинаково распределенных случайных измерений, начинается с расчета описательных статистик эмпирического ряда: средних, медианы, моды, дисперсии, стандартного отклонения, ошибки среднего и др. Особое место в анализе выборок занимает проверка соответствия характера эмпирического распределения какому-нибудь заданному закону распределения. Это связано с тем, что многие стандартные методы статистического анализа предполагают нормальное распределение данных (или не сильно от него отклоняющееся). Работа выполняется по вариантам. Вариант задания соответствует номеру в списке студентов журнала посещений. Скопируйте выборку, соответствующую номеру вашего варианта, в новую книгу MS Excel и сохраните в своей папке. Средние значения pH атмосферных осадков (в первой строке номер варианта) 1 7,20 2 7,00 3 5,64 4 3,78 5 3,40 6 7,22 7 7,05 8 6,84 9 6,53 10 2,90 11 7,49 12 2,30 13 6,40 14 5,70 15 5,80 3,70 6,88 5,39 4,92 6,30 7,17 7,06 6,56 6,96 4,80 7,55 7,80 6,85 5,48 3,60 3,70 6,88 4,72 6,51 4,40 6,61 6,73 6,96 7,02 5,14 7,23 5,90 6,91 5,19 2,00 2,90 6,75 7,63 7,58 4,90 7,05 6,78 6,78 7,00 5,90 7,55 3,10 6,80 5,99 2,70 3,80 6,88 3,80 2,69 6,40 7,20 6,53 6,88 6,93 6,80 7,21 3,60 6,40 5,39 3,70 4,70 7,25 6,44 2,96 6,20 6,85 7,05 7,87 6,85 4,90 7,19 4,70 6,55 5,70 3,40 4,80 6,88 7,10 2,06 6,70 6,95 7,06 7,33 7,04 4,30 7,14 2,60 6,31 5,39 2,30 3,90 7,00 6,29 8,47 5,10 6,88 6,97 7,13 7,03 5,20 7,30 4,00 6,59 5,01 2,60 5,60 6,88 3,80 7,23 7,00 6,93 7,02 7,08 7,08 5,90 6,67 2,60 6,86 5,60 2,60 4,50 7,42 3,29 3,56 7,50 6,80 7,02 6,98 6,88 4,94 6,90 2,90 7,24 4,50 3,90 3,90 7,25 4,72 2,34 6,10 6,53 7,07 6,96 6,85 4,30 6,98 3,00 6,63 5,39 3,30 4,00 7,00 3,29 8,24 8,20 4,91 7,24 6,89 6,87 4,10 6,90 2,20 6,55 4,38 2,96 4,70 7,08 3,11 8,19 8,40 7,02 7,24 6,86 6,70 3,67 7,06 7,80 7,17 6,11 2,50 6,60 6,13 6,89 5,06 5,30 7,02 7,13 6,86 7,97 7,20 7,14 6,30 6,86 5,77 2,30 4,70 6,75 1,50 3,65 5,40 6,85 7,25 6,93 7,18 5,20 7,21 2,30 6,55 4,79 3,70 3,90 7,13 6,89 4,51 5,60 6,88 7,37 7,51 7,97 5,80 7,57 2,00 6,21 4,61 3,00 3,80 7,13 1,50 4,34 3,90 6,86 6,77 6,97 6,64 4,30 8,13 1,70 7,17 4,87 2,20 4,30 7,89 7,59 2,17 4,30 6,87 7,04 6,84 7,10 6,10 7,26 2,90 6,68 4,50 3,00 6,50 7,00 7,04 3,65 3,60 6,93 7,07 7,44 6,70 4,80 7,20 5,10 6,55 4,38 1,90 7,50 7,43 5,88 3,66 3,20 7,80 6,02 6,73 6,29 3,40 7,25 3,80 6,68 5,52 3,40 3,90 6,88 3,29 6,89 3,60 6,89 6,78 7,45 7,17 5,30 7,48 4,30 6,62 4,55 4,20 4,30 6,88 8,88 1,83 4,10 6,85 6,98 6,83 7,14 4,40 7,23 3,20 6,68 4,61 1,70 3,90 6,50 5,67 2,87 3,90 7,35 6,88 7,05 6,85 3,57 7,60 3,80 6,55 5,86 2,10 3,80 6,67 3,80 4,20 4,40 7,13 6,97 6,99 7,13 4,00 8,34 3,20 6,68 5,94 2,30 5,40 6,50 6,11 1,91 4,10 7,14 6,88 7,05 6,96 5,00 7,43 3,20 6,31 4,38 2,30 5,10 7,25 5,59 3,63 5,20 7,41 6,87 7,12 7,09 5,10 7,56 4,60 6,91 4,32 2,70 4,70 6,75 4,54 2,15 6,60 7,19 7,19 6,85 7,11 4,20 7,37 3,40 6,48 6,09 2,10 6,70 6,88 4,54 1,97 6,80 7,78 7,34 6,83 7,11 5,20 7,43 3,90 6,86 6,21 3,90 4,30 6,88 7,36 7,78 8,90 7,27 7,09 6,94 7,21 4,80 7,46 3,00 6,55 5,63 2,90 5,90 6,88 3,98 3,23 5,80 7,29 7,89 6,65 6,94 4,50 8,09 2,60 6,31 5,80 2,50 16 2,26 17 1,79 18 3,89 19 2,87 20 2,52 21 2,64 22 2,88 23 2,72 24 2,11 25 2,30 26 3,77 27 2,72 28 2,45 29 3,77 30 5,30 3,14 1,66 3,05 2,91 2,70 2,38 3,03 4,18 2,82 2,87 2,61 3,02 1,95 4,34 5,45 3,58 2,66 3,89 2,92 3,69 2,88 3,65 2,43 2,45 3,14 3,10 3,16 3,82 3,13 5,38 3,14 1,36 3,09 2,46 3,56 2,03 2,58 2,76 3,36 2,35 2,44 4,21 3,34 3,44 6,73 3,05 1,91 4,44 3,47 3,09 2,74 3,34 2,76 2,76 3,87 4,48 3,48 3,12 2,93 6,64 2,45 1,40 3,38 2,52 2,40 2,52 2,79 2,92 3,26 2,64 3,76 3,45 2,76 5,20 5,70 2,45 0,72 3,00 2,34 2,57 2,27 2,53 2,55 2,27 3,15 3,05 3,11 3,29 3,16 5,38 2,73 1,42 3,23 2,13 2,64 2,36 2,71 2,43 2,43 2,40 3,82 2,68 2,56 2,45 6,31 3,22 2,45 4,26 2,96 2,94 1,77 1,97 3,56 4,04 2,76 2,90 3,51 3,21 2,73 5,52 3,05 3,56 3,37 2,43 2,70 2,98 2,16 3,64 4,29 4,93 3,25 2,57 4,48 3,81 5,58 3,35 2,94 4,17 2,92 2,34 3,26 3,29 2,57 2,81 2,00 3,77 2,66 4,39 3,87 3,64 2,95 2,13 3,53 2,92 2,16 2,80 2,43 3,24 3,99 2,66 3,71 2,44 3,46 4,25 5,63 3,05 3,33 3,76 3,71 2,30 3,16 2,62 2,62 3,70 2,45 2,87 2,39 4,24 3,28 5,45 3,25 2,03 2,77 2,76 2,60 2,53 2,34 2,52 3,69 2,88 3,78 2,27 3,96 3,54 4,09 2,85 2,74 3,22 3,05 2,25 5,28 2,13 2,07 4,14 2,21 4,20 2,66 2,60 4,52 5,45 3,05 2,00 3,47 2,62 2,92 2,37 2,28 3,83 2,70 2,54 3,25 3,26 1,85 4,31 4,55 2,85 2,81 4,59 2,37 2,22 3,59 5,99 2,79 3,50 3,12 3,25 2,72 2,08 2,85 3,62 3,18 3,50 3,78 3,23 2,72 3,09 2,25 4,59 3,94 3,23 2,98 2,88 4,06 3,22 3,91 2,81 1,53 3,33 2,57 2,37 3,43 2,76 2,91 3,50 3,50 3,17 2,44 3,49 3,79 4,25 2,95 1,51 3,78 2,94 2,72 3,32 2,16 2,72 2,65 1,95 2,78 2,39 3,55 3,71 4,25 2,85 1,47 3,50 2,94 2,43 2,61 2,57 3,16 2,47 2,20 3,00 2,36 3,10 3,48 5,06 2,81 2,07 4,98 2,83 2,14 2,78 2,30 3,66 2,40 3,75 2,79 2,21 3,99 3,01 4,61 2,73 2,35 4,75 4,37 3,43 2,19 2,16 3,05 3,44 3,24 3,03 2,42 3,78 4,41 4,61 2,92 1,75 3,18 2,62 2,52 3,43 3,09 3,00 3,29 3,83 3,21 2,61 4,46 5,22 4,32 3,18 1,87 4,29 2,60 3,63 3,79 3,75 3,10 2,77 3,45 2,44 2,78 4,75 3,93 4,91 3,40 2,07 4,68 2,55 2,40 2,88 2,83 3,52 3,05 2,78 2,93 3,10 2,56 3,64 4,96 3,30 3,21 5,78 2,60 4,09 2,11 3,15 3,49 2,69 1,79 2,61 3,22 2,75 2,75 5,12 2,73 1,43 4,55 2,37 2,97 2,34 2,46 3,46 4,54 3,55 3,11 2,72 3,14 3,14 4,50 4,65 2,15 3,26 2,40 2,38 2,66 2,13 3,74 3,78 2,90 2,83 3,50 4,53 4,53 6,74 3,25 0,72 4,45 3,01 2,58 2,37 2,96 1,99 3,96 2,62 3,70 1,95 4,91 4,91 5,21 3,18 2,10 3,95 2,67 2,87 3,51 2,70 2,62 2,51 2,62 3,18 3,26 6,12 6,12 4,50 Построение гистограммы с помощью инструмента «Гистограмма» надстройки «Анализ данных» Microsoft Excel Гистограмма представляет собой столбчатую диаграмму частот. По горизонтальной оси диаграммы откладывают измеренные значения из набора данных, по вертикальной – частоту встречаемости этих значений. Высота каждого столбца показывает частоту (количество) значений из набора данных, принадлежащих соответствующему интервалу, равному ширине этого столбца. Гистограмма наглядно показывает, какие значения или диапазоны значений исследуемой переменной являются наиболее частыми, насколько сильно они различаются между собой, как сконцентрировано большинство наблюдений вокруг среднего, является распределение симметричным или нет, имеет ли оно моду или несколько мод (т.е. мультимодальным). Для построения гистограммы в Excel используют инструмент Гистограмма из Пакета анализа. При этом весь диапазон изменения случайной величины разбивается на интервалы равной ширины, называемые карманами (классами). Подсчитывается число выборочных значений, попавших в каждый карман. По ним вычисляются статистические (относительные) частоты - отношение числа попаданий в карман m к общему числу испытаний n (m/n), по которым и строится гистограмма выборочной функции распределения статистических вероятностей. Определим объем выборки. Устанавливаем курсор в ячейку, где будет приведено значение N (к примеру, С2), выполняем команду Вставить функцию из меню Формулы, далее в категориях Статистические выбираем функцию СЧЁТ, нажимаем ОК. В появившемся окне нажимаем на кнопку напротив поля Значение 1. Выделяем ячейки с данными (A2:A31) и жмем ОК. Аналогичным способом находим наименьшее (команда МИН(А2:А31) и наибольшее =МАКС(А2:А31). Оценим величину классового интервала (i) при которой ряд не был бы слишком громоздким и, в тоже время, позволил бы выявить характерные черты случайной величины x по формуле: i = (хmax – xmin) / k, где k – количество интервалов. Для оценки оптимального количества интервалов можно воспользоваться формулой Стерджесса: k = 1 + 3,3 lg n, где n — количество всех значений величины. Рис. 1. Вычисление ширины интервала Определим границы интервалов. За начало первого интервала рекомендуется принимать величину, равную a1 = (xmin – i / 2), тогда a2 = a1 + i, a3 = a2 + i и т. д. (рис. 2). Построение интервалов продолжают до тех пор, пока начало следующего по порядку интервала не будет равным или большим xmax. При необходимости уменьшите разрядность. Рис. 2. Расчет границ интервалов Для расчета интервальных частот и построения гистограммы воспользуемся инструментом Гистограмма из надстройки Анализ данных Microsoft Excel. По умолчанию данная надстройка не установлена, поэтому для ее активации необходимо открыть Параметры Excel (Файл – Параметры) и выбрать вкладку Надстройки. В поле Управление выберите элемент Надстройки Excel и нажмите кнопку Перейти. Откроется диалоговое окно Надстройки, в нем установите флажок для компоненты Пакет анализа. После нажатия кнопки ОК меню Данные будет дополнено командой Анализ данных. В окне ввода исходных данных инструмента Гистограмма (рис. 3) укажите входной интервал (ссылку на ячейки A2:A31; выделять заголовок столбца и отмечать флажок Метки не будем), интервал карманов (ссылку на ячейки C8:C14, содержащие правые границы интервалов), установите флажок автоматического вывода графика, задайте выходной интервал. Рис. 3. Диалоговое окно Гистограмма Отредактируйте полученную гистограмму. Исключите зазоры, выполнив следующие действия: Нажмите правую кнопку мыши на одном из столбиков гистограммы, выберите Формат ряда данных. В открывшемся окне на вкладке Параметры ряда установите Без зазора. Рис. 4. Гистограмма Вычислите коэффициент вариации (V), представляющий собой отношение среднего квадратического отклонения к средней арифметической, выраженное в процентах (=СТАНДОТКЛОН (A2:A31) / СРЗНАЧ (A2:A31)*100). Коэффициенты асимметрии (Kas) и эксцесса (Е) относятся к показателям формы распределения. Величина Kas может быть положительной и отрицательной. Положительная величина коэффициента асимметрии указывает на наличие правосторонней асимметрии, отрицательная – левосторонней. Оцените Kas с помощью среднеквадратической ошибки коэффициента асимметрии, которая зависит от объема изучаемой совокупности и 6( N 1) рассчитывается по формуле: mas . ( N 1)( N 3) Если отношение Kas/mas > 3, то асимметрия считается существенной. Рис. 5. Формулы для оценки асимметрии Аналогично оценим коэффициент эксцесса (Е) (рис. 6). Ошибка коэффициента 24 N ( N 2)( N 3) эксцесса: mE . Если отношение E/mE > 3, то отклонение от ( N 1) 2 ( N 3)( N 5) нормального распределения можно считать существенным. Рис. 6. Формулы для оценки эксцесса Произведите расчет базовых статистических показателей может производиться с использованием надстройки (опции) «Пакет анализа», которая позволяет оперативно получить значения показателей описательной статистики. Выставление показателя метки помечает столбцы или строки, при этом первые значения в расчете не участвуют. Отчет выполните в MS Word, скопировав полученные результаты расчетов и гистограмму. На основании рассчитанных значений показателей описательной статистики и гистограммы сделайте выводы об особенностях формы распределения единиц совокупности. Оцените вариабельность (разброс) значений выборки по величине коэффициента вариации. Возможность отнесения кривой распределения исследуемых данных к типу кривых нормального распределения устанавливается путем анализа формы гистограммы ряда распределения с учетом оценок показателей особенностей формы распределения – коэффициентов асимметрии (Кas) и эксцесса (E). При анализе формы гистограммы прежде всего следует оценить распределение вариантов значений признака по интервалам (группам). Если на гистограмме четко прослеживаются два-три колебания частот вариантов, это говорит о том, что распределение не является однородным. Если гистограмма имеет одновершинную форму, есть основания предполагать, что выборка является однородной по данному признаку. Установив по виду диаграммы однородность совокупности, для дальнейшего анализа формы распределения используются описательные параметры выборки – показатели центра распределения (M, Мо, Ме), вариации (σ), особенностей формы распределения (Кas, E), позволяющие оценить близость эмпирических данных к нормальной форме распределения. Нормальное распределение является симметричным, если для него выполняются соотношения: М = Мо = Ме, Кas = 0. Нарушение этих соотношений свидетельствует о наличии асимметрии распределения. Распределение с небольшой или умеренной асимметрией в большинстве случаев по своему типу относится к нормальному. Отклонение эмпирического ряда по асимметрии и эксцессу от нормального распределения считают существенным, если Kas и Е более, чем в 3 раза превышают свои ошибки (mas, mE).