Формула Пика
реклама

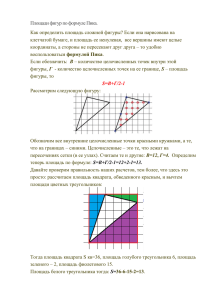
IX школьная научно-практическая конференция «В начале славных дел…» Секция точных наук: Математика. Формула Пика Исследовательская работа по математике Выполнила: Шукалова Кристина Алексеевна, ученица 6А класса МБОУ СШ №1 Научный руководитель : Щербакова Татьяна Прокопьевна, учитель математики МБОУ СШ №1 г. Архангельск, 2016 год 1 Оглавление 1.Ведение………………………………………………………………………………. 3 2.Основная часть………………………………………………………………………. 4 2.1 Представление о Формуле Пика……………………………………. 4 2.2 Об авторе Формулы Пика……………………………….................... 4 2.3 Примеры применения формул……………………………………….. 5 2.4 Вычисления площади фигуры……………………………………….. 6 2.5 Получение дробных площадей………………………………………. 6 2.6 Рассмотрение разных многоугольников с равными площадями……………………………………………………………… 6 2.7 Задача на вычисление площади Открытого банка заданий ЕГЭ по математике сайта ФИПИ ………………………………………….. 7 3.Заключение…………………………………………………………………………… 8 4.Библиографический список………………...……………………............................ 9 5.Приложение……………………………………………………………...................... 10 2 Введение На уроках математики мы учились вычислять площадь прямоугольников, треугольников, многоугольников разрезанием на части и достраиванием их до целых фигур. Мне стало интересно, а можно ли находить площадь многоугольников другим способом? Нами были изучены литература по теме, материалы из интернет источников и проведено исследование. Актуальность: умение находить площадь многоугольников необходимо на уроках математики, а также оно понадобится в будущем, в быту, знание нахождения площади понадобится ещё последующих классах при сдаче экзаменов. Целью нашего исследования является особенности применения нового способа нахождения площади различных многоугольников с вершинами в узлах решетки. Для достижения поставленной цели решались следующие задачи: Изучить источники на бумажных носителях и в Интернете. Провести анализ найденных материалов. Решить задачи на нахождение площади многоугольников разными способами и сравнить результаты. Найти задачи по вычислению площади на клетчатой решётке на сайте ФИПИ. Написать текст исследовательской работы. Объект исследования: нахождение площади многоугольников разными способами. Предмет исследования: Использование Формулы Пика при вычислении площади многоугольника При проведении исследования была выдвинута рабочая гипотеза: нахождение площади одной и той же фигуры разными способами должно давать одинаковые значения. При исследовании использовались следующие методы: Анализ источников, наблюдение, знаковое моделирование, проведение экспериментов, прогнозирование при выдвижении гипотезы. 3 Основная часть 2.1 Представление о Формуле Пика Рассмотрим многоугольник, вершины которого находятся в узлах решётки. Через В обозначаем количество точек, находящихся во внутренней области многоугольника. Через Г обозначаем количество точек на границе многоугольника. Тогда площадь многоугольника находится по формуле S = В + Г/2 – 1. [2] <Приложение 1.> <Приложение 1.> Эту формулу вывел австрийский математик Георг Пик. 2.2 Об авторе Формулы Пика Георг Алекса́ндр Пик родился 10 августа 1859г. в городе Лейпциг. В 16 лет Георг окончил школу и поступил в Венский университет. Широкую известность получила теорема Пика, открытая им в 1899 году для расчёта площади многоугольника. В Германии эта теорема включена в школьные учебники. Умер 13 июля 1942г. в концлагере. [2] <Приложение 2.> Георг Пик 4 2.3 Примеры применения формул Рассмотрим задачу на нахождение площади многоугольника по Формуле Пика: S B B - количество точек внутри. Г 1 2 Г – количество точек на границе. [4] В нашей задаче внутри расположении 17 точек, а на границе -14 точек, тогда площадь многоугольника равна: S =17 + 14 : 2 – 1 = 17 + 7 – 1 = 23. <Приложение 1.> 2.4 Из первых опытов по вычислению площади фигуры Формулу Пика мы подвергли сомнению, так как подсчитали площадь этого же многоугольника вторым способом, разбив его на прямоугольник и два прямоугольных треугольника. Получили, что площадь многоугольника равна 23, а по Формуле Пика у нас получилось 22. Такого расхождения не должно было бы быть, подумали мы. Стали искать ошибку и нашли её. Значит, для этого многоугольника эта формула справедлива. <Приложение 3.> 5 2.5 Получение дробных площадей Мы стали выяснять, существуют ли площади, меньшие единицы при вычислении по Формуле Пика. Рассмотрели многоугольники, у которых нет точек во внутренней области. Для синего треугольника площадь равна ½, а для красного треугольника площадь равна 3/2. Значит, можно построить треугольники, с площадью меньше единицы, и треугольник с площадью, больше единицы. Даже получилось, что можно построить треугольник с площадью равной единице, если на границе взять четыре точки: S = 0 + 4/2 – 1 = 1. <Приложение 4.> Наши опыты показали, что значение площади по формуле Пика являются либо правильными, либо неправильными дробями со знаменателем 2. 2.6 Рассмотрение разных многоугольников с равными площадями Рассмотрим несколько многоугольников, у которых количество внутренних точек одинаково и количество точек на границе тоже одинаково, а многоугольники имеют разную форму. При этом условии оказалось, что вычисленные площади по формуле Пика равны. S1 = S2 = 13 +6:2 -1 = 15. 6 Рассмотрим многоугольники, у которых количество внутренних точек и точек на границе изменилось и многоугольники имеют разную форму, а площади, вычисленные по формуле Пика, равны. S3 = S4 = 12 +8:2 -1 = 15. Из этих опытов по вычислению площадей мы сделали вывод, что четырёхугольники путём сдвига двух вершин можно заменить на треугольник с такой же площадью. S5 = 12 +8:2 -1 = 15. <Приложение4> 2.7. Задача на вычисление площади Открытого банка заданий ЕГЭ по математике сайта ФИПИ Задача №0AB9AB План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м × 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах. [5] <Приложение5> Г Найдём площадь по формуле Пика: 𝑆 = 𝐵 + 2 − 1. В = 7 , Г = 9. S =7 + 9 : 2 -1= 21 . 2 7 3. Заключение В результате исследования были изучены источники на бумажных носителях и из Интернета. Проведены опыты по применению Формулы Пика для вычисления площадей различных многоугольников. Выявлены возможные ошибки при её применении. Проведены эксперименты по сравнению скорости вычисления площадей многоугольников по формуле Пика и разбиением фигуры на части. Нашли свойство многоугольников, которые можно заменить на равновеликий многоугольник и даже треугольник. Наше исследование подтвердило гипотезу, достигло цели. Полученные результаты можно использовать на занятиях математического кружка и в старших классах при сдачи выпускного экзамена. Исследование можно продолжить в направлении поиска других формул и способов нахождения площади. При выполнении исследовательской работы я узнала много нового, научилась новым приёмам при поиске иллюстраций, получила положительный опыт в преодолении трудностей. 8 4. Библиографический список 1. Математика. 6 класс: учеб. для общеобразоват. учреждений / [С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин]. – 7-е изд. – М. : Просвещение, 2009. – 256 с. 2. Георг Пик https://ru.wikipedia.org/wiki/%D0%9F%D0%B8%D0%BA,_%D0%93%D0%B5%D0%BE%D1%80%D 0%B3 Режим доступа 28.12.15 3. Математические эпюды http://www.etudes.ru/ru/etudes/pick/ Режим доступа 27.01.2016 4. Математика на клетчатой бумаге. Математический клуб «Кенгуру». Выпуск №8. 5. Открытый банк заданий ФИПИ. Режим доступа: http://www.fipi.ru/content/otkrytyy-bankzadaniy-ege 6. Фигуры и площади. Математический клуб «Кенгуру». Выпуск №17. 9 5. Приложения Приложение 1. Выделение точек на границе и во внутренней области многоугольника. . Приложение 2. Портрет Георга Пика 10 Приложение 3. Опыт № 1. Первые ошибки в применении Формулы Пика. Приложение 4. Получение площади, меньшей единицы и большей единицы, по Формуле Пика. 11 Приложение 5 Многоугольники разной формы с равными площадями, полученные путём сдвига вершин. Приложение 6 Чертёж к задаче Открытого банка заданий ЕГЭ по математике сайта ФИПИ 12