Конспект урока по математике «Функция у = aх2, её график и

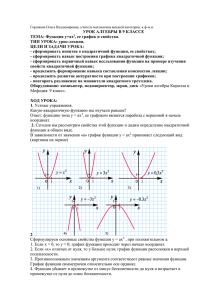
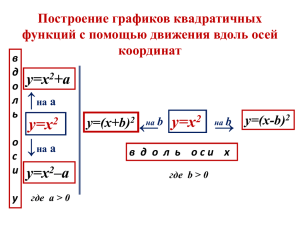
Конспект урока по математике «Функция у = aх2, её график и свойства» для 9-го класса
Тип урока: урок открытия новых знаний.
Цель урока:
1. Формирование учебно-познавательных компетенций через анализ и сравнение различных алгоритмов;
применять имеющиеся знания в новой ситуации, выявлять возникающие проблемы.
2. Формирование коммуникативных компетенций: умение вести диалог, задавать вопросы, защищать свою точку зрения.
Задачи:
- закрепить умения учащихся по построению графиков квадратичной
квадратичной функции от значений а;
функций; выяснить зависимость положения графика
- научить определять по значению а положение ветвей параболы на координатной плоскости; определять промежутки возрастания
и убывания функции; по графику научить определять заданную функцию;
- по формуле квадратичной функции научить определять соответствующий ей график.
Применяемые методы и педтехнологии: исследовательские с использованием компетентностно-ориентированных заданий,
учебный диалог, технология обучения в сотрудничестве; дифференцированный подход к обучению; информационные технологии как
средство активизации познавательной деятельности и творческого потенциала учащихся.
Формы работы: фронтальная, индивидуальная, групповая.
Формируемые компетенции:
- учебно-познавательная;
- коммуникативная.
Формируемые УУД:
- познавательные;
- регулятивные;
- коммуникативные.
Средства обучения: учебник «Алгебра – 9» под редакцией Теляковского, проектор, экран, ноутбуки, Интернет, чертёжные
инструменты.
ХОД УРОКА
№
Этап урока
1
Орг. момент
2
Мотивация
3
Актуализация
и
фиксирования
индивидуально
го затруднения
в
пробном
действии
Название используемых ЭОР
Деятельность учителя
(с указанием действий с ЭОР, например, демонстрация)
Учитель приветствует учащихся и проверяет визуально
готовность к уроку.
Посмотрите внимательно на карточку (приложение 1) и
скажите, а можете ли вы определить, какой функции, какой
график соответствует?
Чем, на ваш взгляд, отличаются эти функции?
Откройте тетради, запишите число, классная работа, тему
урока: «Функция у= ах2, её свойства и график».
http://learningapps.org/display У вас на ПК открыта веб- страница, выполните задание.
?v=7t6bebk5
Сформулируйте вопросы, на которые вы бы хотели
получить ответы на сегодняшнем уроке.
Деятельность ученика
Приветствует учителя,
готовится к уроку
Заслушивает варианты
ответов учащихся
Выполняют задание,
формулируют вопросы:
Что является графиком
функции у= ах2. Как
строится график этой
функции
Какими свойством
обладает заданный
график
http://www.yotx.ru/default.aspx Прежде, чем отвечать на поставленные вопросы, вспомним Каждая группа
?clr0=000000&exp0=2x-3&mix=- основные свойства линейной функции.
выполняет построение
10&max=10&asx=on&u=mm&nx Класс делится на три группы. Каждая группа выполняет графика с помощью
=X&aiy=on&asy=on&ny=Y&iw=6 задание: Постройте график функции:
онлайн - сервиса.
00&ih= 400&ict=png&aa=on
1. y = 2х- 3,
Выполняют
2. y = -2х- 3
предложенное задание
3.y=0,5х+2
на исследование
По графику определите:
линейной функции.
Область определения
Область значения
Нули функции
Определите возрастающей или убывающей является
данная функция.
5. Сколько точек достаточно взять, чтобы построить
график?
Проверим, что у вас получилось. К доске выходят по
одному учащемуся из группы.
Итак, подведём итог: Назовите свойства линейной функции
Для того, чтобы выяснить, что является графиком функции
у=ах2 и какими свойствами она обладает, проведем
исследовательскую работу.
Исследовательская работа.
Построим в одной системе координат график функции
у=ах2, 1) если а=1, и 2) а=0,5. Какую функцию мы получим.
Это квадратичная функция?
Запишем
определение:
Квадратичной
функцией
называется функция, которую можно задать формулой
вида у= ах2+bх+с, где х- независимая переменная, а, b, снекоторые числа, причём а≠0.
1.
2.
3.
4.
4
Изучение
нового
материала
Что надо знать для построения графика функции?
а) С чего начнём построение?
Обсуждают в группе
свои предположения,
доказывают свой выбор.
Подводят итог
у=х2
Записывают
определение
Записывают задания в
тетрадях.
Координаты точек
С построения таблицы
Построим таблицу значений. Для её построения возьмём значений.
побольше точек.
х
-3
-2
-1
0
1
2
3
Озвучивают выводы:
у
9
4
1
0
1
4
9
Построим график функции.
Графиком функции
б) Ответьте на вопросы:
является парабола
Графиком функции является….
Где расположена вершина параболы?
Как проходит график если х=0, и у=0?
http://files.schoolcollection.edu.ru/dlrstore/e5b3b
05d-32e8-4a44-a00a5e9e4a90f087/a09.swf
Исследуйте, как значение коэффициента а влияет на форму
параболы
Если х=0, у=0, график
проходит через начало
координат.
Ветви располагаются
вверх, если х≠0, у>0
Как располагаются ветви параболы, если коэффициент
принимает положительные значения?
Какая ось является осью симметрии параболы?
Относительно оси
ординат
Что значит, парабола симметрична относительно оси Противоположным
ординат?
значениям аргумента
соответствует, равные
значения функции
На каком промежутке функция убывает?
Функция убывает в
промежутке (-∞;0]
Функция возрастает в
На каком промежутке функция возрастает?
промежутке [0;+∞).
Какое наименьшее значение принимает функция?
Наименьшее значение
функции 0, при х=0.
Существует ли наибольшие значение функции?
Нет
Какова область значения функции?
[0;+∞).
Что
происходит
с
графиком
при
увеличении График сжимается
коэффициента?
При уменьшении коэффициента?
График расширяется
http://kvantmultfilm.ru/de_ma
l.php?en=14
Проверим, верны ли наши выводы. Просмотрим Просматривают
видеоролик. В ходе просмотра фиксируйте у себя в видеоролик, определяют
тетрадях все новые для вас термины, фамилии ученых, новые термины.
прозвучавшие с экрана, это вам понадобиться для
выполнения домашнего задания.
Подведём итог.
http://learningapps.org/display
?v=7t6bebk5
Вернёмся в начало урока и заполним пропустившиеся Выполняют
слова
http://files.schoolcollection.edu.ru/dlrstore/46b09
de7-4f94-4ca8-acbfca727e94403b/a08.swf
http://fcior.edu.ru/card/12731/k
vadratichnaya-funkciya.html
Давайте снова посмотрим на карточку (приложение 1) и
выполним предложенное задание: Подберите
математическую запись функции для каждого графика.
Выполняют
Вам необходимо выполнить самостоятельно за
компьютером интерактивный тест с выбором варианта
ответов.
Для тех, кто справится с работой раньше остальных,
предлагаю выполнить задание по карточке
Выполняют тест,
анализируют
полученный результат и
выставляют отметку.
5
6
Физминутка
Первичное
закрепление
нового
материала
7
Самостоятельн http://uztest.ru/lessons#
ая работа
8
Рефлексия
Предлагает ответить на вопросы – ромашка Блума:
1. Простые вопросы: Какие понятия темы тебе
запомнились?
2. Уточняющие вопросы: Правильно ли я вас поняла,
что, графики квадратичной функции важны для
человека?
3. Интерпретирующий вопрос: Почему же график
квадратичной функции так интересен для нас?
4. Практический вопрос: Где мы можем использовать
параболу в повседневной жизни?
5. Творческий вопрос: Если бы вы были
древнегреческим учёным, то как бы обозначали
параболу?
Учащиеся,
справившиеся с тестом,
выполняют
дополнительное
задание.
Отвечают на
поставленные вопросы
Оценивают свою
деятельность на уроке
На сколько вы усвоили данный материал? Оцените
результат своей деятельности.
10
Домашнее
задание
http://youtube.com/watch?v=F
bapCwqQ65A&feature=relate
d
П.5 № 91, 92
Для самостоятельного повторения теоретического
материала просмотреть видеоролик
Творческое задание: на сайте http://wikipedia.org найти
термины, прозвучавшие в ролике (парабола,
параболическое зеркало, телескоп с рефлектором, с
коническое сечение), найти биографии математиков
(Апполоний Пергский, Дж. Грегори), имена которых были
упомянуты.
Подготовить материал к созданию совместного
фотоальбома: сделать фотографии окружающих
предметов, имеющих параболическую форму, выложить
их на сайте FANstudio.