Лабораторная работа № 11 ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ ПРИ НАГРЕВАНИИ И

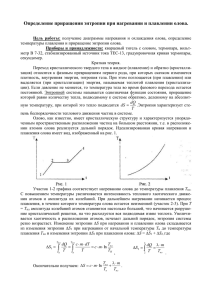
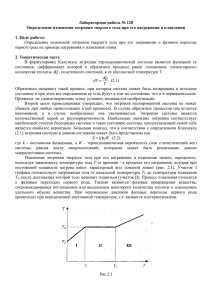
Лабораторная работа № 11
ОПРЕДЕЛЕНИЕ ИЗМЕНЕНИЯ ЭНТРОПИИ ПРИ НАГРЕВАНИИ И
ПЛАВЛЕНИИ ОЛОВА
Цель работы: построить графики плавления и кристаллизации олова;
определить температуру плавления олова; рассчитать изменение энтропии
при фазовом переходе первого рода.
Введение
Понятие энтропии является одним из основных в термодинамике.
Физический смысл энтропии можно пояснить следующими рассуждениями о
направлении тепловых процессов. Если проходит какой-либо тепловой
процесс, то обратный процесс, при котором проходятся те же тепловые
состояния, но в обратном порядке, как правило, невозможен.
P≠ 0
P= 0
Рис.1
Так, необратимо расширение газа в пустоту (рис.1). Газ никогда сам по себе
не соберется вновь в одной половине сосуда. Так же необратим процесс
теплопередачи; тепло передается от более нагретого тела
к
менее
нагретому, но обратный процесс – самопроизвольный переход тепла от
менее нагретого тела к более нагретому - никогда не происходит. Вообще
всякая предоставленная самой себе система стремится перейти в состояние
теплового равновесия, при котором давление и температура одинаковы во
всех частях системы. Достигнув этого состояния, система сама по себе из
него уже не выходит.
Необратимы все процессы, сопровождающиеся трением. Трение вызывает
замедление движения, т.е. приближение к состоянию равновесия, в котором
отсутствует движение одних частей относительно других. При этом
кинетическая энергия направленного движения постепенно исчезает,
превращаясь в тепло, точнее, во внутреннюю энергию системы - энергию
хаотического движения молекул соответствующего равновесного состояния.
Тот факт, что все самопроизвольные тепловые процессы идут только в
одном направлении - к тепловому равновесию, в физике известен как второй
закон (второе начало) термодинамики.
Итак, необратимы все тепловые процессы, однако степень необратимости
зависит от характера конкретного процесса. В некоторых случаях степень
необратимости может оказаться столь незначительной, что процесс можно
считать обратимым. Из рассмотренных примеров видно, что для достижения
обратимости следует исключить процессы, имеющие характер приближения к
тепловому равновесию: не должно происходить расширения газа в пустоту,
непосредственного перехода тепла от более нагретого тела к менее нагретому
и не должно быть трения.
Примером обратимого процесса является адиабатическое расширение
(или сжатие) газа. Адиабатический процесс-это процесс, протекающий при
полной
теплоизоляции
от
окружающей
среды.
Условие
теплоизолированности исключает передачу тепла от более нагретых внешних
тел. Если расширяется газ в цилиндре под поршнем и поршень движется
достаточно медленно, то за поршнем не успевает образовываться пустота и
расширение газа в пустоту также не происходит. Разумеется, на практике
всегда останутся какие-то источники необратимости (несовершенство
теплоизоляции, трение при движении поршня), и только если ими пренебречь,
то идеализированный таким образом процесс будет полностью обратим.
Причину необратимости тепловых процессов объясняет теория
вероятности. Дело в том, что вероятность реализации равновесного состояния
(с более хаотичным и, следовательно, более равномерным распределением
молекул по объему системы) выше, чем вероятность неравновесного
состояния. Поясним это арифметическим подсчетом. Пусть в сосуде,
мысленно разделенном на две половины, находится две молекулы №1 и №2.
Ввиду полной хаотичности движений каждая
из них может оказаться в любой части сосуда
с одинаковой вероятностью, В результате с
равной вероятностью могут реализовываться
представленные
на
рис.2
четыре
комбинации распределения молекул
по
частям
сосуда, т.е. четыре различных
микросостояния. Следовательно, вероятность
Рис.2
каждого
микросостояния
равна
1/4.
Отметим, что второе и третье состояния физически эквивалентны (они
неразличимы с макроскопической точки зрения, т.к. нумерация молекул –
процедура чисто умозрительная, молекулы невозможно различить). Поэтому
говорят, что два микросостояния (второе и третье) представляют собой одно
макросостояние II, определяемое термодинамической вероятностью W ,
равной 2 (и вероятностью w = 1/4 + 1/4 =1/2).
Термодинамическая вероятность W состояния системы – это число способов,
которыми может быть реализовано данное макросостояние, или число
микросостояний,
осуществляющих
данное
макросостояние.
Термодинамическая вероятность W =2 означает, что данное физическое
состояние реализуется двумя микроскопическими способами. Проще говоря,
макросостояние II (с более равномерным распределением молекул по объему
сосуда) реализуется вдвое чаще, чем неравномерное распределение I и III.
Рассмотрим теперь четыре молекулы в таком сосуде, мысленно пронумеруем
их. Нетрудно видеть, что теперь ввиду хаотичности движения молекул
возникает равновероятная возможность реализации 16 микросостояний
(рис.3).
Однако и здесь можно выделить группы физически эквивалентных
состояний, т.е. макросостояний с соответствующей термодинамической
вероятностью W . Это следующие макросостояния: I (W =1), II (W =4), III (
W =6) равновесное, IV (W =4), V (W =1). Теперь термодинамическая
вероятность
равновесного распределения III выше, чем вероятность
наиболее неравновесного распределения I или V уже в шесть раз.
Рис.3
С ростом числа молекул в сосуде вероятность наиболее
неравновесного распределения, когда все молекулы собираются в одной
половине сосуда, резко убывает: для двух молекул w =1/22=1/4 (рис.2) для
четырех молекул w =1/24=1/16 (рис.3), для N молекул w =1/2N (при N
=1020: w  0 ). При этом термодинамическая вероятность равновесного
состояния с ростом числа молекул все больше превосходят вероятность
любого неравновесного состояния.
Итак, система стремится к равновесному состоянию, поскольку именно
оно обладает наибольшей термодинамической вероятностью W =6. Это
надо понимать
так: если возможно другое состояние, у которого
термодинамическая вероятность больше, то система будет стремиться к
этому состоянию.
В физике, однако,
принято пользоваться не самим значением
термодинамической вероятности W , а ее логарифмом, умноженным на
постоянную Больцмана k . Определенную таким образом величину S как
S  k lnW ,
(1)
называют энтропией системы.
Энтропия так же, как и термодинамическая вероятность, определяет
направление тепловых процессов. Если возможно состояние с большей
энтропией, то система будет стремиться к этому новому состоянию.
Второй закон термодинамики, определяющий направление тепловых
процессов, можно сформулировать, поэтому как закон возрастания энтропии:
при любых необратимых процессах в замкнутой системе энтропия системы
возрастает. Максимально возможное значение энтропия
достигает в
тепловом равновесии.
Справедливо и обратное. Всякий процесс, при котором энтропия
замкнутой системы возрастает, является необратимым. Чем больше
возрастание энтропии, тем больше степень необратимости, и наоборот.
Идеализированному случаю полностью обратимого процесса в замкнутой
системе соответствует изменение энтропии, равное нулю. Разумеется, если
система не замкнута, то ее энтропия изменяется и при обратимом процессе.
Определение энтропии по формуле (1) представляет сложную задачу
статистической физики. Соответствующие расчеты позволяют связать
энтропию с другими тепловыми величинами. Запишем без вывода формулу
для расчета изменения dS энтропии при бесконечно малом элементарном
обратимом процессе:
dS 
dQ
,
T
(2)
где dQ - количество тепла, полученное системой (незамкнутой), T температура системы. Связь dS и dQ по формуле (2) имеет простой
физический смысл. Сообщение системе тепла приводит к увеличению
хаотичности теплового движения, хаотичности распределения молекул
(выравниванию распределения по объему) и, следовательно, к увеличению
термодинамической вероятности W или энтропии S . Естественно и то, что
на изменение энтропии dS подведенная энергия dQ влияет тем больше, чем
меньше собственная внутренняя энергия системы, пропорциональная
температуре T . Поэтому с уменьшением температуры dS возрастает.
Экспериментальная часть
Процесс плавления и последующего охлаждения олова можно
представить на графике зависимости его температуры от времени нагревания
(рис.4). По мере сообщения теплоты температура олова сначала повышается,
а затем, когда олово нагреется до температуры плавления Tпл , несмотря на
продолжающееся нагревание, его температура остается неизменной. Когда
олово полностью расплавится, температура жидкого олова будет снова
повышаться. При охлаждении расплавленного олова температура сначала
понижается, затем начинается кристаллизация, которая происходит также
при неизменной температуре.
4
T
2
3
5
6
1Т
7
t
0
Рис.4
Плавление (кристаллизация) представляют собой фазовый переход
вещества из твердой фазы в жидкую (и наоборот). Фазовый переход 1 рода
сопровождается поглощением или выделением теплоты при неизменной
температуре. Вся поглощенная при плавлении теплота пойдет на
совершение работы по разрушению кристаллической решетки, поэтому
температура остается постоянной до тех пор, пока не расплавится весь
кристалл. Дальнейшее нагревание пойдет на увеличение кинетической
энергии молекул жидкого олова, и температура снова будет повышаться. При
охлаждении температура будет понижаться до тех пор, пока не начнется
кристаллизация. Выстраивая кристаллическую решетку, атомы олова
возвращают в виде теплоты ту энергию, которая была затрачена на ее
разрушение при плавлении. Таким образом, Tпл = Т кр .
Определение изменения энтропии при плавлении олова будем определять
по формуле (2). Так как в процессе плавления олово нагревают, то
количество подведенного тепла положительное dQ >0, следовательно,
изменение энтропии также положительно dS >0. Это значит, что энтропия
олова в жидком состоянии больше, чем в кристаллическом состоянии.
Увеличение энтропии объясняется тем, что в жидком состоянии движение
молекул более хаотизированно по сравнению с твердым состоянием.
Определим изменение энтропии олова Sн при нагревании его от
комнатной температуры
плавления):
Sн
Tк
до температуры плавления
Т пл
Т пл dQ
.
  dS  
Тк T
Тк
Tпл
(до начала
(3)
Количество тепла, полученное оловом при нагревании, пропорционально
изменению температуры: dQ  cmdT (4), где c – удельная теплоемкость
олова ( c =230 Дж/кг К), а m – масса олова.
Подставляя (4) в (3), получаем:
Т пл dT
Tпл cmdT
T
Sн  
 cm 
 cm ln пл .
Тк
Тк T
Тк T
Найдем изменение энтропии олова Sпл в процессе
(5)
плавления. В этом
случае температура олова не изменяется, несмотря на подведение тепла. Все
тепло идет на работу по разрушению кристаллической решетки.
Sпл  
dQ
1
Q
m


,
 dQ 
Tпл Т пл
Tпл Tпл
(6)
где
Q  m - количество тепла, переданное олову при плавлении, а  
Q
m
-
удельная (приходящаяся на единицу массы) теплота плавления олова
(  = 0,58 х 105 Дж/кг).
Полное приращение энтропии к концу плавления:
Т

.
S  Sн  Sпл  mc ln пл 
Т к Т пл
(7)
Формула (7) может быть использована для экспериментального
определения изменения энтропии при нагревании и плавлении олова после
измерения значения температур Tпл и Tк .
Экспериментальная установка
Для определения изменения энтропии при нагревании и плавлении олова
предназначена экспериментальная установка ФПТ1-11, общий вид которой
показан на рис.4. Нагревание олова происходит в тигле с помощью
электрического нагревателя 3, источник питания которого размещен в блоке
приборов 7. Температура олова измеряется термопарой 6 с помощью
цифрового термометра, расположенного в блоке 7. Время нагрева измеряется
цифровым секундомером, расположенным в блоке приборов 7.
Рис.4. Общий вид экспериментальной установки ФПТ1-11 и ее блок-схема:
1-стойка, 2-кронштейн, 3-нагреватель, 4-датчик температуры, 5-тигель с исследуемым
материалом, 6-блок рабочего элемента, 7- блок приборов
Порядок выполнения работы
1.Включить установку тумблером «Сеть» и измерить начальную температуру
олова Tк .
2.Одновременно включить нагреватель и запустить секундомер и через
каждую минуту измерять температуру олова. Измерения проводить до тех
пор, пока температура не достигнет постоянной величины ( Tпл ), а затем
начнет увеличиваться. Результаты измерений отмечать на графике T =f(t).
3.Выключить нагреватель и провести аналогичные измерения при
охлаждении олова, отмечая температуру на том же графике, что и в п.2.
4.Выключить установку тумблером «Сеть».
Обработка результатов измерения
1.По двум полученным графикам определить температуры, соответствующие
участкам графиков, параллельным оси времени, и по их среднему значению
найти температуру плавления (кристаллизации) олова.
2.По формуле (7) определить изменение энтропии за время нагревания и
плавления олова.
3.Оценить погрешность результатов измерений.
Контрольные задания
1.Дать определение фазовому переходу первого рода? Что характерно для
этого перехода?
2.Что такое энтропия и как она связана с термодинамической вероятностью?
3.Сравнить изменение энтропии при нагревании и плавлении олова и из чего
складывается полное изменение энтропии?
4.Вывести основную расчетную формулу, используемую в данной работе.
5.До какой температуры нужно нагревать олово в тигле при выполнении
эксперимента?
6.Обьяснить причину необратимости тепловых процессов. В каком
направлении идут тепловые процессы?
7.Каковы основные источники погрешностей данного метода измерений?
Литература
1. Трофимова Т.И. Курс физики. - М.Высшая школа, 1999-2003.
2. Савельев И.В. Курс общей физики, М.: - Наука, 2002, т.II.
3. Детлаф А.А., Яворский Б.М. Курс Физики, М.: - Высшая школа,2002
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Дальневосточный государственный технический университет
(ДВПИ им. В.В.Куйбышева)
Определение изменения энтропии при нагревании и плавлении олова
Методические указания к лабораторной работе № 11
для студентов дневной и заочной форм обучения всех технических
специальностей по курсу физики
Владивосток , 2009
Одобрено научно-методическим советом университета
УДК 536.625; 076.
Определение изменения энтропии при нагревании и плавлении олова: метод.
указания /сост.В.В.Зауткин, Г.П.Тимакова, Н.И.Чухрий. - Владивосток: Издво ДВГТУ, 2009.-9с.
Методические указания предназначены для проведения лабораторного
практикума по курсу общей физики для студентов дневной и заочной форм
обучения
@ Зауткин В.В., Тимакова Г.П., Чухрий Н.И. 2009