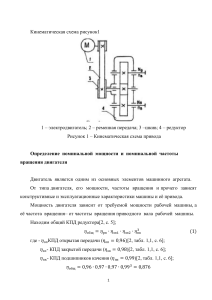
12АТП-1
реклама

Группа 12 АТП-1
Дата 05.02.2016
Дисциплина МДК.06.01 Основы машиностроительного производства
Задание: Изучить материалы изложенные в практической работе № 37
Методика расчета конической прямозубой передачи.
Исходными данными для расчета конической прямозубой передачи являются
требуемое передаточное отношение, передаваемые моменты на валах шестерни
и колеса, частота вращения шестерни и колеса.
Все эти величины должны быть определены после выбора двигателя и
кинематического расчета механизма.
Расчет конической прямозубой передачи с межосевым углом
Σ=90○производится в следующей последовательности.
1. Выбор материала зубчатых колес.
При выборе материалов шестерни и колеса можно руководствоваться данными,
приведенными в таблице 1 Приложения. Рекомендуется выбирать материалы и
термообработку таким образом, чтобы твердость поверхности зубьев шестерни
была на 20÷30 НВвыше, чем колеса.
2. Определение допускаемых напряжений.
С учетом фактических условий нагружения:
;,
где [σ]HO, [σ]FO- допускаемые соответственно контактные и изгибные
напряжения при базовом числе циклов напряжений (таблица 1) ;
m = 6 - для колес из незакаленных сталей и других мягких материалов ;
m = 9 - для колес из закаленных сталей;
NHO , NFO- базовые числа циклов нагружений;
NHE, NFE- фактические числа циклов нагружений за заданный срок службы.
При расчете на контактную прочность зубьев принимается
NHO =30HB24[1] .
При расчете на изгиб зубьев для зубчатых колес, выполненных из сталей NFO =
4×106 , для зубчатых колес из других материалов NFO=3×106.
При расчете NHE =NFEисходят из того, что за каждый оборот колеса каждый
зуб испытывает один цикл нагружений
NHE = NFE = 60×n ×T,
где n– частота вращения зубчатого колеса, об/мин;
Т– время работы передачи за срок службы механизма, в часах.
Если NHE<NHOилиNFE<NFO, то принимают соответственно
NHE =NHO и NFE=NFO .
Если NHE>25×107,NFE>25 ×107, то принимаютNHE=NFE =25×107.
В обоих случаях следует пересчитать срок службы передачи, исходя из
принятых значений NHE и NFE.
3. Определение чисел зубьев шестерни, колеса и передаточнго числа.
Число зубьев шестерни по условию отсутствия подрезания для прямозубых
колес должно быть Z1 ≥ 17 cos(90o- arctg ί 12),
где ί 12 - требуемое передаточное отношение передачи ( отношение угловых
скоростей шестерни и колеса).
Рекомендуется выбирать Z1 = 18 ÷ 30.
Число зубьев колеса Z2=Z1 × ί 12 .
Передаточное число u = Z2 /Z1 , определяется по найденным значениям
Z1иZ2, округленных до целых чисел, и не должно отличаться от требуемого
передаточного отношения более, чем на3%.
4. . Определение внешнего делительного диаметра колеса
Из условия контактной прочности рабочих поверхностей зубьев:
,
где M2- вращающий момент на колесе ,H/мм;
u - передаточное число зубчатой передачи;
[σ]HE - наименьшее допускаемое контактное напряжение с учетом
фактических условий нагружений;
ψвRе = в/Re ≤0,3 - коэффициент ширины зубчатого венца, при выполнении
проектного расчета рекомендуется принимать ψвRе= 0,285 ;
KH - коэффициент нагрузки, учитывающий дополнительные вредные нагрузки,
сопутствующие работе передачи. При проектном расчете предварительно
принимают KH = 1,2 для колес с твердостью поверхностей зубьев HB≤350 и KH
=1,35 при твердости HB>350.
E1, E2- модули упругости первого рода соответственно материала шестерни и
колеса.
Полученное значение dе2 округляют до ближайшего стандартного значения по
ГОСТ 12289-76 (таблица 2).
1.5. Расчёт геометрических параметров зубчатой передачи
Геометрические параметры конического зацепления
Внешний окружной модуль me = dе2 ⁄Z2.
Угол делительного конуса колеса δ2 = arctg u.
Угол делительного конуса шестерни δ1 = 90○ - δ2 .
Внешний делительный диаметр шестерни dе1 = m e1×Z1 .
Внешнее конусное расстояние Re = 0,5 de2 ⁄ sin δ2 .
Ширина зубчатого венца b = ΨвRе × Re.
Среднее конусное расстояние R = Re – 0,5 b.
Средний окружной модуль m = me R ⁄ Re .
Средний делительный диаметр шестерни d1 = m ×Z1 .
Средний делительный диаметр колеса d2 = m × Z2 .
Внешняя высота зуба he = 2,2 ×me .
Внешняя высота головки зуба hae = me .
Внешняя высота ножки зуба hfe = 1,2 ×me.
Угол ножки зуба θf = arc tg ( hfe ⁄ Re).
Угол головки зуба θd = θf.
Внешний диаметр вершин зубьев шестерни dae1 = de1+ 2hae ×cos δ1.
Внешний диаметр вершин зубьев колеса dae2 = dae2 + 2hae×cos δ2.
1.6. Проверочный расчёт контактных напряжений на рабочих поверхностях
зубьев
Кнβ - коэффициент концентрации нагрузки, учитывающий распределение
нагрузки по ширине венца, определяется по таблице 3.
Кнν - коэффициент, учитывающий влияние динамической нагрузки, влияющей
в зацеплении, определяется в зависимости от степени точности зубчатых колес,
твердости рабочей поверхности зубьев о окружной скорости по
таблицам 4 и 5.
Если полученное в результате расчета фактическое контактное напряжение σн
не превышает допускаемое напряжение [σ]HE более чем на 5%, т.е.
ξ= σн-[σ] НЕ/[σ] HE× 100% ≤ 5%,
то прочность зубчатой передачи по контактным напряжениям можно считать
удовлетворительной. Если же расхождение ξ >5%, то необходимо увеличить
внешние делительные диаметры зубчатых колес de2 и de1 или подобрать для
изготовления зубчатых колес материал, обеспечивающий более высокое
значение [σ]HE. В зависимости от принятого решения производятся вновь
необходимые расчеты в соответствии с данной методикой.
1.7. Определение сил в коническом зацеплении.
Окружные усилия на шестерне и колесе Ft1=Ft2=2M1/d1=2M2/d2.
Радиальная сила на шестерне, равная осевой силе на колесе
Fr1=2M1×tgλ×cos b1/ d1,
где угол зацепления λ=200.
Осевая сила на шестерне, равная радиальной силе на колесе
Fa1=2M1×tgλ× sin b1/d1= Fr2.
1.8. Проверочный расчет зубьев на выносливость по напряжениям изгиба
σF = (Ft×KFв×KFν×YF )/(0,85×b×m) ≤ [σ]FE,
где КFβ- коэффициент концентрации нагрузки, учитывающийнеравномерность
распределения нагрузки по длинезубьев, определяется по таблице 6.
KFν – коэффициент динамичности, учитывающий динамическое действие
нагрузки, определяется по таблице 7.
YF – коэффициент прочности зубьев по местным напряжениям, определяется по
таблице П8 в зависимости от эквивалентного числа зубьев на колесе
(шестерни)Z ν= Z / cos b.
Расчет следует вести для зубьев того из колес, для которого отношение
[σ]FЕ/YFменьше.
Если полученное в результате фактическое напряжение изгиба σF не превышает
допускаемое [σ]FЕ или превышает, но не более чем на 5%, т.е.
ξ = {(σF -[σ]FЕ)/ [σ]FЕ´} 100% ≤ 5%,
прочность зубьев по напряжениям изгиба можно считать удовлетворительной.
Если же ξ>5%, то необходимо увеличить внешние делительные диаметры
зубчатых колес de2 и de1 или подобрать для изготовления зубчатых колес
материал, обеспечивающий более высокое значение [σ]HЕ. В зависимости от
принятого решения производятся вновь необходимые расчеты в соответствии с
данной методикой.
2. пример расчета.
Рассмотрим пример расчета конической прямозубой передачи с межосевым
углом 90о. Такие конические зубчатые передачи получили наибольшее
распространение.
Для наглядности в настоящем разделе один и тот же расчёт выполнен дважды: с
микрокалькулятором «вручную» и на компьютере.
Оба расчета используют одни и те же исходные данные: вращающие моменты
на валу шестерни М1и валу колесаМ2, частота вращения шестерниn1,
передаточное число передачи и срок службы передачи. Кроме того, в исходных
данных должен указывается способ расположения колес относительно опор на
валах.
Исходные данные.
Необходимо рассчитать реверсивную прямозубую коническую зубчатую
передачу. Вращающий момент на валу колеса М2 = 61400 Н/мм. Частота
вращений шестерниn1 = 1500 об/мин. Требуемое передаточное отношение
передачиi12=2,12. Срок службыТ = 103часов. Шестерня расположена
относительно опор консольно, а колеса несимметрично.
2.1. Расчет на калькуляторе.
2.1.1. Выбор материала зубчатых колес.
Так как заданием не предусматривается специальных требований к габаритам и
массе передачи, выбираем в качестве материала для изготовления зубчатых
колес сталь со средними механическими характеристиками и относительно
небольшой стоимостью – сталь 45 ГОСТ 1050-74. для шестерни – сталь 45,
термообработка – улучшениеНВ 220; для колеса – сталь 45, термообработка –
нормализацияНВ 190. Учитывая реверсивность передачи (зубья работают
обеими сторонами), по таблице 1 определяем допускаемые контактные и
изгибные напряжения, соответствующие базовому числу циклов напряжений.
[σ]но1=600Н/мм2, [σ]но2=500Н/мм2, [σ] FO 1=180Н/мм2, [σ] FO 2=140Н/мм2 .
2.1.2. Расчёт допускаемых напряжений с учетом фактических условий
нагружения.
Фактическое число циклов нагружений зубьев шестерни и колеса:
NHE1=NFЕ1=60×n1×T=60×1500×103=9×107;
NHE2=NFЕ2=60×n1×T/ί12=60×1500×103/2,12=4,2×107.
Базовые числа циклов нагружений:
Nно1=30НВ2,4=30×2202,4=1,2×107,
Nно2=30×1902,4=0,88×107;
NFO1=NFO2=4×106.
Допускаемые контактные напряжения:
Допускаемые напряжения изгиба:
2.1.3. Определение чисел зубьев и передаточного числа.
Принимаем Z1=20. Тогда число зубьев колеса Z2=Z1×ί12=20×2,12=42,4.
Принимаем Z2=42. Передаточное число зубчатой передачи равно
u=Z2/Z1=42/20 = 2,10, что вполне приемлемо, так как относительная ошибка
меньше 1%.
2.1.4. Определение внешнего делительного диаметра колеса
Из условия контактной прочности рабочих поверхностей зубьев:
,
В качестве расчетного допускаемого контактного напряжения принимаем
наименьшее, т.е. [σ]НЕ=[σ]НЕ2=385 Н/мм2.
Коэффициент нагрузки предварительно принимаем КН=1,2;
модуль упругости первого рода для сталей Е=Е1=Е2=2,1×105Н/мм2(таблица 1).
Коэффициент ширины зубчатого венца принимаем ψвRе=0,285.
Принимаем в соответствии с ГОСТ 12289-76 (таблица 2) de2=180мм.
2.1.5. Расчёт геометрических параметров зубчатой передачи.
Внешний окружной модуль me= de2/Z2=180/42=4,285мм.
Углы делительных конусов колеса и шестерни:
b2 = arctgu = arctg 2,1 = 64032´12´´,
b1= 900- b2 = 900-64032´12´´= 25027´48´´.
Внешний делительный диаметр шестерни de1= me Z1=4,285×20=85,75мм.
Внешнее конусное расстояние
Re=0.5 de2/sin b2=0.5×180/sin 64032´12´´=99,68мм.
Ширина зубчатого венца в=ψвRе×Re=0,285×99,68=28,408мм.
Принимаем в=28мм.
Среднее конусное расстояние R=Re-0,5в=99,68-0,5×28=85,476мм.
Средний окружной модуль m=me R/Re=4,285×85,476/99,68=3,674мм.
Средние делительные диаметры шестерни и колеса:
d1=m× Z1=3,674×20=73,48мм,
d2=m× Z2=3,674×42=154,31мм.
Внешняя высота зуба hе=2,2× me =2,2×4,285=9,427мм.
Внешняя высота головки зуба hαе= me =4,285мм.
Внешняя высота ножки зуба hƒе=1,2× me =1,2×4,285=5,142мм.
Угол ножки зуба θƒ= arctg( hƒе/ Re) = arctg (5,142/99,68) = 2057´12´´
Угол головки зуба θα = θƒ = 2057´12´´.
Внешние диаметры вершин зубьев шестерни и колеса:
dαе1=dα1+2hαе×cos b1=85,70+2×4,285×cos 25027´48´´ =93,44мм,
dαе2= dα2+2 hαе ×cos b2=180+2×4,285×cos 64032´12´´=183,68мм.
2.1.6. Проверочный расчет контактных напряжений на рабочих поверхностях
зубьев
;
Коэффициент ширины шестерни по среднему диаметру
Ψвd =в/d 1=28/73,48=0,38,
а средняя окружная скорость ν=πd1×n1/60000=π×73,48×1500/60000=5,8 м/с.
Для этой скорости по таблице 5 назначаем 8-юстепень точности.
По таблице 3 при Ψвd=0,38, консольном расположении шестерни и твердости
поверхности зубьев НВ < 350 коэффициент КНβ=1,15.
Коэффициент КНΝ=1,1определяется по таблице 5.
2.1.7. Определение сил в зацеплении.
Окружная сила Ft=2M2 /d2=2×51400/154.31=795,80 H.
Радиальная сила на шестерне, равное осевому усилию на колесе
Fr1= Fa2=2M2tg200×sind2/b2=2×61400×tg200sin 64032´12´´/154,32 = 261,44 Н.
Осевая сила на шестерне, равная радиальной силе на колесе
Fa1=2M1×tgλ× sin b1/d1= Fr2. =2×21162×tg200sin25 027´48´´/73,48= 123,12 Н.
2.1.8. Проверочный расчет зубьев на выносливость
по напряжениям изгиба
Рассчитываем эквивалентное число зубьев шестерни и колеса
Zν1=Z1/cosb1=20/cos25027´48´´=22,15
Zν2=Z2 /cos b 2=42/cos 64032´12´´=97,68;
Значения YF1=4,1иYF2=3,6определяем по таблице 8.
Рассчитываем и сравниваем отношения
[σ]FЕ1/YF1=107/4,1=26,09; [σ]FЕ2/YF2=95/3,6=26,38.
Расчет ведем для зубьев шестерни, т.к. [σ]FЕ1/YF1<[σ]FЕ2/YF2.
по таблице 6 КFβ=1,37, а по таблице 7КFν=1,45.