пропорциональные отрезки в прямоугольном - Matem

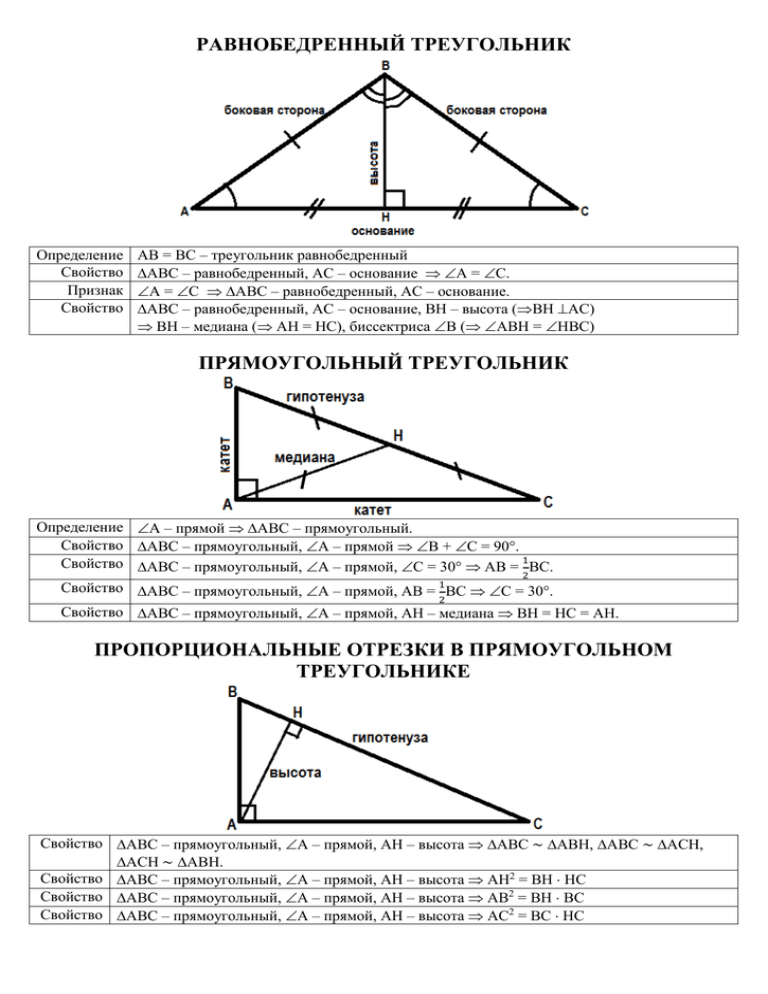
РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК
Определение
Свойство
Признак
Свойство
АВ = ВС – треугольник равнобедренный
АВС – равнобедренный, АС – основание  А = С.
А = С  АВС – равнобедренный, АС – основание.
АВС – равнобедренный, АС – основание, ВН – высота (ВН АС)
 ВН – медиана ( АН = НС), биссектриса В ( АВН = НВС)
ПРЯМОУГОЛЬНЫЙ ТРЕУГОЛЬНИК
Определение А – прямой  АВС – прямоугольный.
Свойство АВС – прямоугольный, А – прямой  В + С = 90.
Свойство АВС – прямоугольный, А – прямой, С = 30  АВ = 1ВС.
2
Свойство АВС – прямоугольный, А – прямой, АВ = 1ВС  С = 30.
2
Свойство АВС – прямоугольный, А – прямой, АН – медиана  ВН = НС = АН.
ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ В ПРЯМОУГОЛЬНОМ
ТРЕУГОЛЬНИКЕ
Свойство АВС – прямоугольный, А – прямой, АН – высота  АВС ~ АВН, АВС ~ АСН,
АСН ~ АВН.
Свойство АВС – прямоугольный, А – прямой, АН – высота  АН2 = ВН  НС
Свойство АВС – прямоугольный, А – прямой, АН – высота  АВ2 = ВН  ВС
Свойство АВС – прямоугольный, А – прямой, АН – высота  АС2 = ВС  НС