ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ПО ГЕОМЕТРИИ В 8 КЛАССЕ

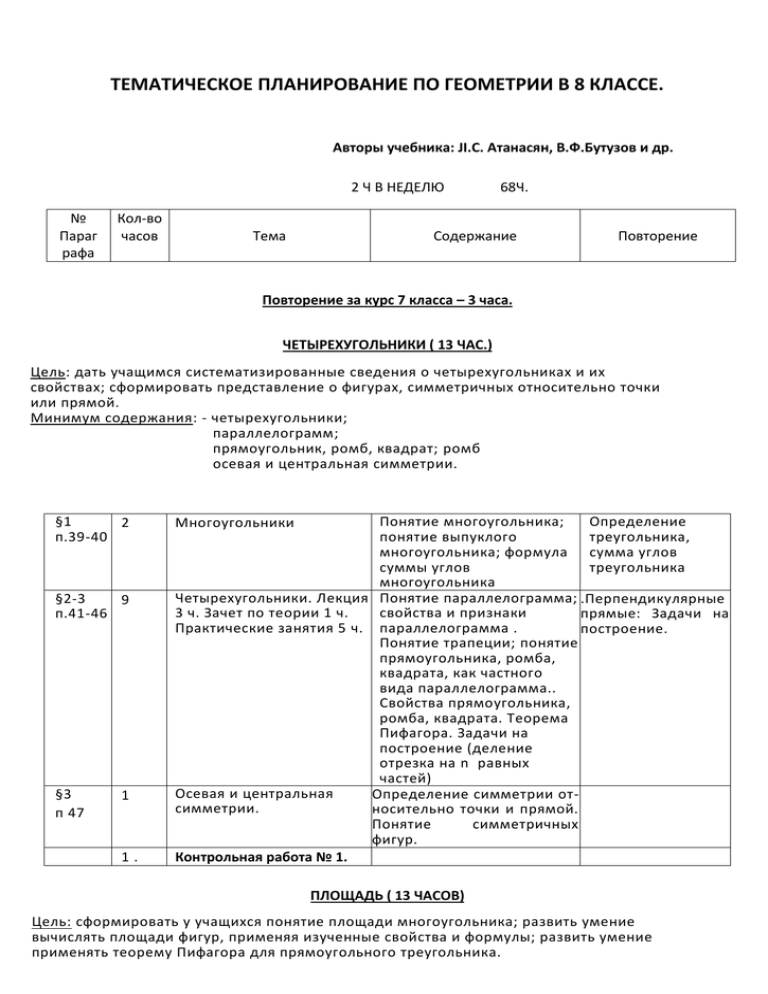
ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ ПО ГЕОМЕТРИИ В 8 КЛАССЕ.
Авторы учебника: JI.C. Атанасян, В.Ф.Бутузов и др.
2 Ч В НЕДЕЛЮ
№
Параг
рафа
Кол-во
часов
Тема
68Ч.
Содержание
Повторение
Повторение за курс 7 класса – 3 часа.
ЧЕТЫРЕХУГОЛЬНИКИ ( 13 ЧАС.)
Цель: дать учащимся систематизированные сведения о четырехугольниках и их
свойствах; сформировать представление о фигурах, симметричных относительно точки
или прямой.
Минимум содержания: - четырехугольники;
параллелограмм;
прямоугольник, ромб, квадрат; ромб
осевая и центральная симметрии.
§1
2
п.39-40
§2-3
9
п.41-46
§3
п 47
1
1.
Понятие многоугольника;
Определение
понятие выпуклого
треугольника,
многоугольника; формула сумма углов
суммы углов
треугольника
многоугольника
Четырехугольники. Лекция Понятие параллелограмма; .Перпендикулярные
3 ч. Зачет по теории 1 ч.
свойства и признаки
прямые: Задачи на
Практические занятия 5 ч. параллелограмма .
построение.
Понятие трапеции; понятие
прямоугольника, ромба,
квадрата, как частного
вида параллелограмма..
Свойства прямоугольника,
ромба, квадрата. Теорема
Пифагора. Задачи на
построение (деление
отрезка на n равных
частей)
Осевая и центральная
Определение симметрии отсимметрии.
носительно точки и прямой.
Понятие
симметричных
фигур.
Контрольная работа № 1.
Многоугольники
ПЛОЩАДЬ ( 13 ЧАСОВ)
Цель: сформировать у учащихся понятие площади многоугольника; развить умение
вычислять площади фигур, применяя изученные свойства и формулы; развить умение
применять теорему Пифагора для прямоугольного треугольника.
Минимум содержания: - площади
четырёхугольников, теорема Пифагора.
§1-2
п 48-53
8
Площади фигур
(многоугольников,
четырёхугольников)
Лекция 2 ч.
Зачет по теории 1 ч.
Практические занятия 5ч.
§3
п54-55
4
Теорема Пифагора.
1
Контрольная работа № 2.
Основные свойства пло- Единицы
щадей. Вывести формулу измерения
для
вычисления площадей
площади
прямоугольника
квадрата,
параллелограмма,
треугольника и трапеции
Формулировка и
Прямоугольный
доказательство
треугольник,
его
теоремы Пифагора и
свойства.
обратной ей теоремы.
!
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ ( 19 Ч А С А )
Цель: сформировать понятие подобных треугольников. Выработать умение применять
признаки подобия треугольников, сформировать аппарат решения прямоугольных
треугольников.
Минимум содержания: - три признака подобия треугольников, средняя линия треугольника.
определения синуса, косинуса, тангенса острого угла прямоугольного треугольника,
значение синуса, косинуса, тангенса для углов 30 ,45 ,60 .
1
§1-2
п56-61
§3
П.62-65
§4
П.66-67
7
Определение подобных
треугольников.
Признаки подобия
треугольников . Лекция
1,5 ч. Зачет по теории
0,5 ч. Практические
занятия 5 ч
Понятие пропорциональных
Определение
отрезков; понятие подобных
биссектрисы угла.
треугольников, изучить
Определение
свойство биссектрисы
равных треутреугольника. Формулировка и гольников.
доказательство признаков
Признаки
подобия треугольников и
равенства
применение этих признаков при треугольников
решении задач.
1
6
Контрольная работа № 3.
Применение подобия к Сформулировать и доказать
доказательству теорем теорему о средней линии
и решению задач
треугольника. Ввести понятие
среднего геометрического двух
отрезков и рассмотреть вопрос
о пропорциональных отрезках в
прямоугольном треугольнике.
Задача на деление отрезка в
данном отношен-
4
Соотношения между
сторонами и углами в
прямоугольном
треугольнике.
Ввести понятия синуса, косинуса
и тангенса острого угла
прямоугольного треугольника.
Применение элементов
тригонометрии для решения
прямоугольных треугольников.
Задачи на построение : деление
отрезка пополам;
построение
перпендикулярных
прямых;
построение ,
биссектрисы угла.
Понятие прямоугольного
треугольника, его
элементы:
теорема
Пифагора.
Нахождение значений
синуса, косинуса и тангенса углов в 30° ,.45°,
60°.
1
Контрольная работа № 4 .
ОКРУЖНОСТЬ (16 ЧАСОВ )
Цель: дать учащимся систематизированные сведения об окружности и ее свойствах,
вписанных и описанных окружностях.
Минимум содержания: - окружность и круг;
касательная к окружности и ее свойства; центральные и вписанные углы; окружность,
описанная около треугольника Окружность, вписанная в треугольник.
§1
П.68-69
3
§2
П.70-71
4
§3
П.72-73
2
§3
П.74-75
4
2
1
4
Взаимное
расположение прямой
и окружности. Понятие
касательной к окружности, свойство
касательной. Свойство
отрезков касательных,
проведенных из одной
точки.
Понятие градусной меры
Центральные и вписанные
дуги окружности.
углы
Понятие центрального и
вписанного углов.
Теорема об измерении
вписанных углов и об
отрезках
пересекающихся хорд.
Четыре замечательные точки Свойство биссектрисы
угла; свойство
треугольника
серединного
перпендикуляра к
отрезку. Ввести четыре
замечательные точки
треугольника.
Понятие вписанной и
Вписанная и описанная
описанной окружности
окружности
около многоугольника.
Теорема об
окружности, вписанной
в треугольник и
описанной около
треугольника. Свойства
вписанных и описанных
четырехугольников.
Решение задач по теме
Решение задач
« Окружность».
Контрольная работа № 5.
Обобщающее повторение
Касательная к окружности
Понятие
окружности и ее
элементы
Свойство внешнего
угла. Свойство равнобедренного
треугольника.
Первый признак
подобия
треугольников.
Медиана,
биссектриса,
высота треугольника.