7 класс - 3 четверть

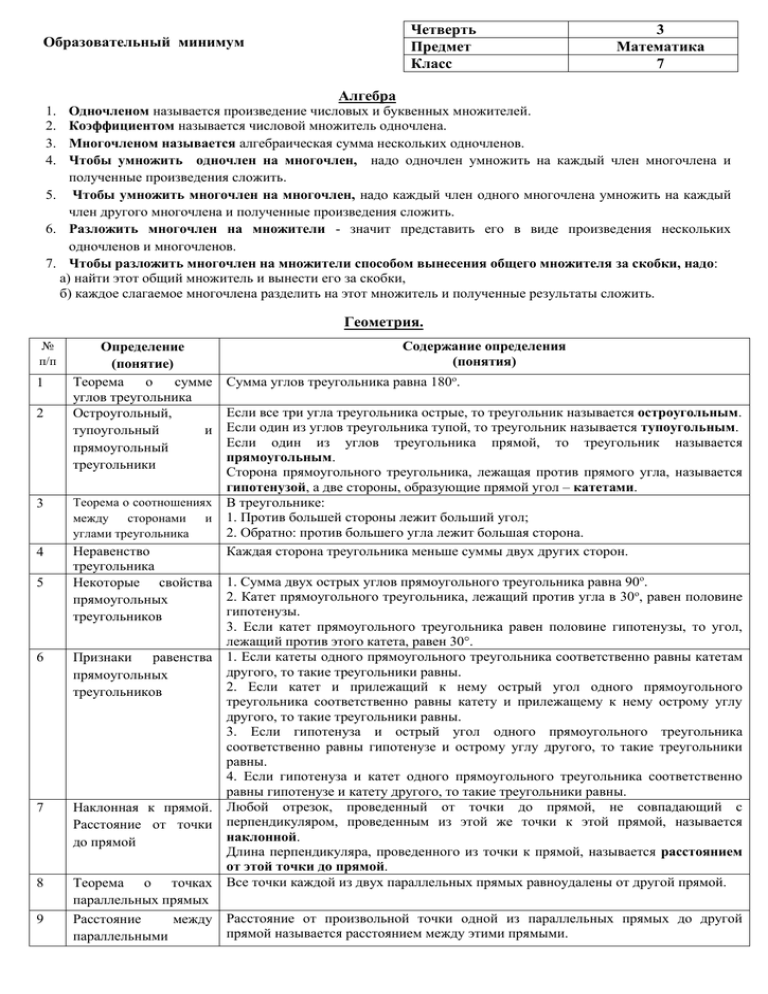
Четверть
Предмет
Класс
Образовательный минимум
3
Математика
7
Алгебра
Одночленом называется произведение числовых и буквенных множителей.
Коэффициентом называется числовой множитель одночлена.
Многочленом называется алгебраическая сумма нескольких одночленов.
Чтобы умножить одночлен на многочлен, надо одночлен умножить на каждый член многочлена и
полученные произведения сложить.
5. Чтобы умножить многочлен на многочлен, надо каждый член одного многочлена умножить на каждый
член другого многочлена и полученные произведения сложить.
6. Разложить многочлен на множители - значит представить его в виде произведения нескольких
одночленов и многочленов.
7. Чтобы разложить многочлен на множители способом вынесения общего множителя за скобки, надо:
а) найти этот общий множитель и вынести его за скобки,
б) каждое слагаемое многочлена разделить на этот множитель и полученные результаты сложить.
1.
2.
3.
4.
Геометрия.
№
п/п
1
2
Определение
(понятие)
Теорема
о
сумме
углов треугольника
Остроугольный,
тупоугольный
и
прямоугольный
треугольники
Содержание определения
(понятия)
Сумма углов треугольника равна 180о.
Если все три угла треугольника острые, то треугольник называется остроугольным.
Если один из углов треугольника тупой, то треугольник называется тупоугольным.
Если один из углов треугольника прямой, то треугольник называется
прямоугольным.
Сторона прямоугольного треугольника, лежащая против прямого угла, называется
гипотенузой, а две стороны, образующие прямой угол – катетами.
В треугольнике:
1. Против большей стороны лежит больший угол;
2. Обратно: против большего угла лежит большая сторона.
Каждая сторона треугольника меньше суммы двух других сторон.
3
Теорема о соотношениях
между сторонами и
углами треугольника
4
Неравенство
треугольника
Некоторые свойства 1. Сумма двух острых углов прямоугольного треугольника равна 90о.
2. Катет прямоугольного треугольника, лежащий против угла в 30о, равен половине
прямоугольных
гипотенузы.
треугольников
3. Если катет прямоугольного треугольника равен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
Признаки равенства 1. Если катеты одного прямоугольного треугольника соответственно равны катетам
другого, то такие треугольники равны.
прямоугольных
2. Если катет и прилежащий к нему острый угол одного прямоугольного
треугольников
треугольника соответственно равны катету и прилежащему к нему острому углу
другого, то такие треугольники равны.
3. Если гипотенуза и острый угол одного прямоугольного треугольника
соответственно равны гипотенузе и острому углу другого, то такие треугольники
равны.
4. Если гипотенуза и катет одного прямоугольного треугольника соответственно
равны гипотенузе и катету другого, то такие треугольники равны.
Наклонная к прямой. Любой отрезок, проведенный от точки до прямой, не совпадающий с
Расстояние от точки перпендикуляром, проведенным из этой же точки к этой прямой, называется
наклонной.
до прямой
Длина перпендикуляра, проведенного из точки к прямой, называется расстоянием
от этой точки до прямой.
Теорема о точках Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
параллельных прямых
Расстояние
между Расстояние от произвольной точки одной из параллельных прямых до другой
прямой называется расстоянием между этими прямыми.
параллельными
5
6
7
8
9
прямыми