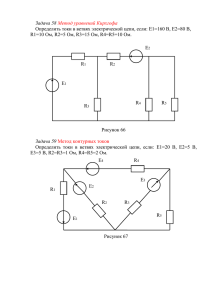
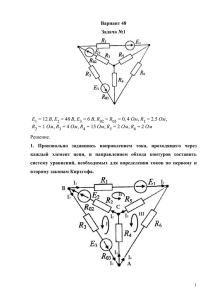
Электротехника и электроника ОПУ14.1, ОПУ
реклама

ЭЛЕКТРОТЕХНИКА И ЭЛЕКТРОНИКА Задание. Составить конспект темы «Законы Кирхгофа. Методы контурных токов и узлового напряжения», ответив на следующие вопросы: 1. Сформулировать первый закон Кирхгофа. Написать закон в математической форме 2. Дать определение: ветвь, узел. 3. Написать правило определения знака тока, для записи первого закона Кирхгофа. 4. Сформулировать второй закон Кирхгофа. Написать закон в математической форме 5. Написать правило определения знака ЭДС, для записи второго закона Кирхгофа. 6. Переписать в тетрадь образец решения задачи на тему «Законы Кирхгофа. Методы контурных токов и узлового напряжения». Ответы на вопросы присылать на электронную почту: [email protected] 1 Законы Кирхгофа – правила, которые показывают, как соотносятся токи и напряжения в электрических цепях. Эти правила были сформулированы Густавом Кирхгофом в 1845 году. В литературе часто называют законами Кирхгофа, но это не верно, так как они не являются законами природы, а были выведены из третьего уравнения Максвелла при неизменном магнитном поле. Но все же, первое более привычное для них название, поэтому и мы будет их называть, как это принято в литературе – законы Кирхгофа. Первый закон Кирхгофа – сумма токов сходящихся в узле равна нулю. Давайте разбираться. Узел это точка, соединяющая ветви. Ветвью называется участок цепи между узлами. На рисунке видно, что ток i входит в узел, а из узла выходят токи i1 и i2. Составляем выражение по первому закона Кирхгофа, учитывая, что токи, входящие в узел имеют знак плюс, а токи, исходящие из узла имеют знак минус i-i1-i2=0. Ток i как бы растекается на два тока поменьше и равен сумме токов i1 и i2 i=i1+i2. Но если бы, например, ток i2входил в узел, тогда бы ток I определялся как i=i1-i2. Важно учитывать знаки при составлении уравнения. Первый закон Кирхгофа это следствие закона сохранения электричества: заряд, приходящий к узлу за некоторый промежуток времени, равен заряду, уходящему за этот же интервал времени от узла, т.е. электрический заряд в узле не накапливается и не исчезает. Второй закон Кирхгофа – алгебраическая сумма ЭДС, действующая в замкнутом контуре, равна алгебраической сумме падений напряжения в этом контуре. 2 Напряжение выражено как произведение тока на сопротивление (по закону Ома). В этом законе тоже существуют свои правила по применению. Для начала нужно задать стрелкой направление обхода контура. Затем просуммировать ЭДС и напряжения соответственно, беря со знаком плюс, если величина совпадает с направлением обхода и минус, если не совпадает. Составим уравнение по второму закону Кирхгофа, для нашей схемы. Смотрим на нашу стрелку, E2 и Е3совпадают с ней по направлению, значит знак плюс, а Е1 направлено в противоположную сторону, значит знак минус. Теперь смотрим на напряжения, ток I1 совпадает по направлению со стрелкой, а токи I2 и I3 направлены противоположно. Следовательно: -E1+E2+E3=I1R1-I2R2-I3R3 На основании законов Кирхгофа составлены методы анализа цепей переменного синусоидального тока. Метод контурных токов – метод основанный на применении второго закона Кирхгофа и метод узловых потенциалов основанный на применении первого закона Кирхгофа. 3 Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач. Задача 1 Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа. Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение. Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС. На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс. Уравнения для первого и второго контуров по второму закону будут: 4 Все эти три уравнения образуют систему Подставим известные значения и решим данную линейную систему уравнений. 100𝐼1 + 150𝐼3 = 75 {150𝐼2 + 150𝐼3 = 100 𝐼3 − 𝐼1 − 𝐼2 = 0 𝐼3 = 𝐼1 + 𝐼2 { 100𝐼1 + 150(𝐼1 + 𝐼2 ) = 75 150𝐼2 + 150(𝐼1 + 𝐼2 ) = 100 Раскроем скобки, умножим второе уравнение на 2, получим: 𝐼3 = 𝐼1 + 𝐼2 {500𝐼1 + 300𝐼2 = 150 150𝐼1 + 300𝐼2 = 100 Из второго уравнения полученной системы выразим 𝐼2 . Вычтем из второго уравнения третье. Получим: 𝐼3 = 𝐼1 + 𝐼2 100 − 150𝐼1 {𝐼2 = 300 350𝐼1 = 50 𝐼1 = 0.14 {𝐼2 = 0.26 𝐼3 = 0.40 Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей. 36.1≈36.5 Баланс мощностей сошелся, а значит токи и ЭДС найдены верно. 5