Тема 4. Стереометрические задачи
реклама

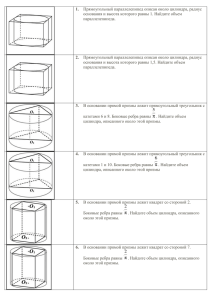
Тема 4. Стереометрические задачи Задания В9 и В11. Для успешного решения предлагаемых задач требуется знание основных формул для нахождения значений геометрических величин пространственных фигур, умения проводить дополнительные построения на изображениях пространственных фигур, работать с формулами, выполнять арифметические действия и преобразования числовых выражений. Задание С2 Характеристика задания Задание на вычисление отрезков, площадей, углов, связанных с многогранниками и телами вращения. Как правило, в задаче нужно найти длину отрезка, площадь, угол (между двумя прямыми, между прямой и плоскостью, между двумя плоскостями), связанные с призмой, пирамидой, цилиндром, конусом или шаром. Дополнительные построения минимальны (например, построение линейного угла двугранного угла). Теоретический материал Площадь поверхности призмы S = S áîê . + 2 S îñí . ., где S áîê . . – площадь боковой поверхности призмы, S îñí . – площадь основания. S áîê .ïðÿìîé ïðèçìû = Ðîñí . H , где Ðîñí . – периметр основания, H – высота призмы, (высота прямой призмы равна боковому ребру). Объем призмы V = S îñí . . * H Площадь поверхности пирамиды S = S áîê . + S îñí . 1 Ðîñí . háîê . , где háîê . – апофема (высота боковой грани Sбок. правильной пирамиды = 2 правильной пирамиды). 1 S îñí . * H 3 Площадь поверхности цилиндра S = S áîê . + 2 S îñí . Объем пирамиды V = Sбок. = 2 RH , S îñí . = R 2 , R – радиус основания цилиндра, H – высота. Объем цилиндра V =. S îñí . H = R 2 H . Площадь поверхности конуса S = S áîê . + S îñí . Sбок. = RL , где L – образующая конуса, R – радиус основания. 1 Объем конуса V = R 2 H . 3 Площадь поверхности шара S = 4 R 2 , 4 Объем шара V = R 3 . 3 Задания для самостоятельной работы Задания В9 1) Найдите квадрат расстояния между вершинами C и D2 многогранника, изображенного на рисунке, все двугранные углы которого прямые. 2) Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 3, а его диагональ равна 29 . Найдите третье ребро параллелепипеда, выходящее из той же вершины. 3)Основанием прямой четырехугольной призмы является ромб со стороной 3 и острым углом 60 0 . Меньшая диагональ призмы равна 5. Найдите боковое ребро призмы. 4) Боковое ребро правильной шестиугольной пирамиды равно 8 и наклонено к плоскости основания под углом 60 0 . Найдите радиус окружности, описанной около основания пирамиды. 5) Радиус основания цилиндра равен 4, диагональ осевого сечения равна 8 2 . Найдите образующую цилиндра. 6. Найдите радиус сферы, вписанной в куб, диагональ которого равна 2 3 . 7.Найдите квадрат диаметра сферы, описанной прямоугольного параллелепипеда, ребра которого равны 3,4,5. Задания В11 1. Площадь поверхности куба равна 54. Найдите его объем. 2. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы. 3. Объем треугольной пирамиды равен 45. Плоскость, проходящая через сторону основания этой пирамиды, пересекает противоположное ребро в точке, делящей это ребро в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые разбивает плоскость исходную пирамиду. 4. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой. 5. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра. 6. Найдите площадь поверхности многогранника, изображенного на рисунке. Все двугранные углы многогранника равны 90 0 . Задания С2 1. В правильной шестиугольной призме ABCDEFA1 B1C1 D1 E1 F1 , все ребра которой равны 2, найдите расстояние от точки B до прямой A1 F1 . 2. В правильной треугольной пирамиде SABC с основанием ABC известны ребра: AB 24 3 , SC 25. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и BC. 3. В кубе ABCDA1 B1C1 D1 найдите косинус угла между плоскостями BA1C1 и BA1 D1 . 4. В правильной треугольной призме ABCA1 B1C1 , все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1 . 5. Основанием прямой призмы ABCDA1 B1C1 D1 является ромб ABCD , AB 10 , BD 12 . Высота призмы равна 6. Найдите расстояние от центра грани A1 B1C1 D1 до плоскости BDC 1. .