НПФ располагает статистикой по смертности среди участников за... времени. Необходимо исследовать насколько фактическая ...
реклама
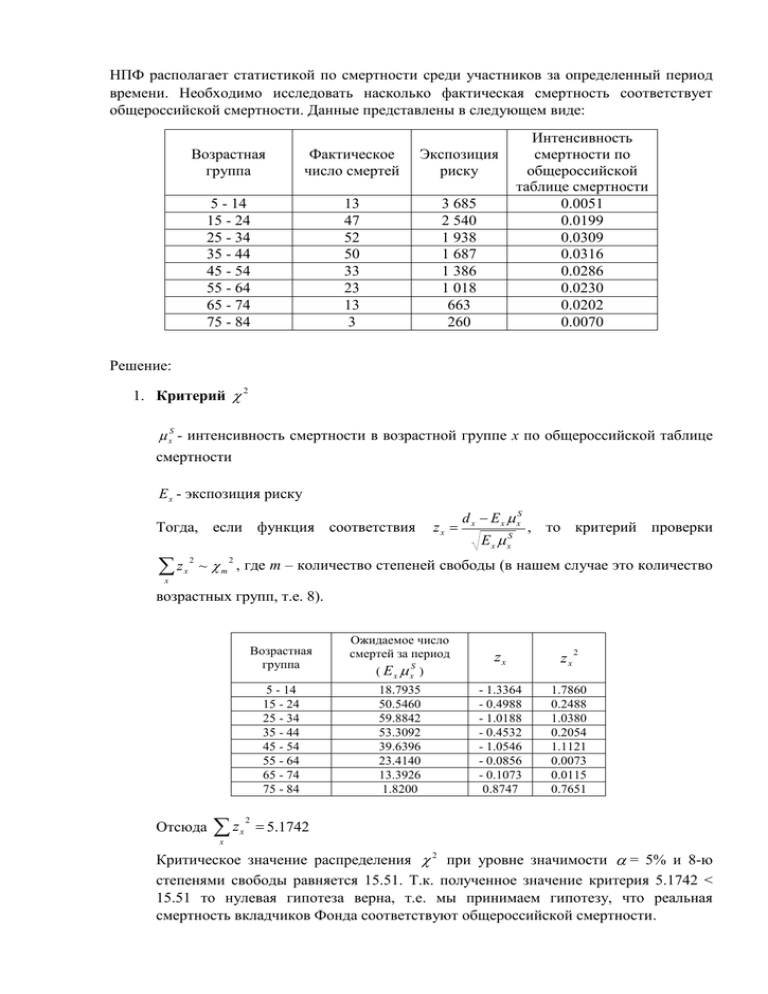
НПФ располагает статистикой по смертности среди участников за определенный период времени. Необходимо исследовать насколько фактическая смертность соответствует общероссийской смертности. Данные представлены в следующем виде: Возрастная группа Фактическое число смертей Экспозиция риску 5 - 14 15 - 24 25 - 34 35 - 44 45 - 54 55 - 64 65 - 74 75 - 84 13 47 52 50 33 23 13 3 3 685 2 540 1 938 1 687 1 386 1 018 663 260 Интенсивность смертности по общероссийской таблице смертности 0.0051 0.0199 0.0309 0.0316 0.0286 0.0230 0.0202 0.0070 Решение: 1. Критерий 2 xS - интенсивность смертности в возрастной группе x по общероссийской таблице смертности E x - экспозиция риску Тогда, если функция соответствия z 2 x zx d x E x xS E x xS , то критерий проверки ~ m , где m – количество степеней свободы (в нашем случае это количество 2 x возрастных групп, т.е. 8). Возрастная группа 5 - 14 15 - 24 25 - 34 35 - 44 45 - 54 55 - 64 65 - 74 75 - 84 Отсюда z 2 x Ожидаемое число смертей за период ( Ex ) S x 18.7935 50.5460 59.8842 53.3092 39.6396 23.4140 13.3926 1.8200 2 zx zx - 1.3364 - 0.4988 - 1.0188 - 0.4532 - 1.0546 - 0.0856 - 0.1073 0.8747 1.7860 0.2488 1.0380 0.2054 1.1121 0.0073 0.0115 0.7651 5.1742 x Критическое значение распределения 2 при уровне значимости = 5% и 8-ю степенями свободы равняется 15.51. Т.к. полученное значение критерия 5.1742 < 15.51 то нулевая гипотеза верна, т.е. мы принимаем гипотезу, что реальная смертность вкладчиков Фонда соответствуют общероссийской смертности. 2. Standardised deviations test Предполагаем, что индивидуальное отклонение распределено нормально Normal (0,1) и поэтому только 1 из 20 z x должен иметь абсолютный разброс значений больше чем 1.96. Т.к. наибольшее отклонение меньше чем 1.96, то принимаем нулевую гипотезу. 3. Signs test Число положительных знаков имеет биномиальное распределение m,0.5 , где m – количество степеней свободы (в нашем случае это количество возрастных групп, т.е. 8). В нашем случае возможен только 1 положительный знак. В соответствии с формулой биномиального распределения вероятность иметь 0 либо 1 положительный знак: 8 8 8 8 0.5 0.5 0.0352 0 1 Т.к. мы используем двусторонний критерий (слишком мало или слишком много положительных знаков могут быть проблемой), то мы отклоняем нулевую гипотезу если вероятность иметь 0 либо 1 положительный знак будет меньше 0.025. Т.к. 0.0352 > 0.025 мы принимаем нулевую гипотезу. 4. Cumulative deviations test (d x x E x xS ) E x xS ~ Normal (0,1) x Возрастная группа d x E x xS 5 - 14 15 - 24 25 - 34 35 - 44 45 - 54 55 - 64 65 - 74 75 - 84 Сумма - 5.7935 - 3.5460 - 7.8842 - 3.3092 - 6.6396 - 0.4140 - 0.3926 1.1800 - 26.7991 Ожидаемое число смертей ( E x xS ) 18.7935 50.5460 59.8842 53.3092 39.6396 23.4140 13.3926 1.8200 260.7991 26.7991 1.6595 . При уровне значимости = 5% значение 260.7991 критерия содержится в интервале 1.96,1.96 . Значения критерия Таким образом, принимаем нулевую гипотезу. 5. Grouping of signs test G = число групп положительных знаков = 1 m = число отклонений = 8 n1 = число положительных отклонений = 1 n2 = число отрицательных отклонений = 7 Необходим определить максимальное K, при котором будет выполнено неравенство: n1 1 n2 1 k t 1 t 0.05 m t 1 n1 Мы отклоняем нулевую гипотезу при уровне значимости 5%, если G K . K = 0. Таким образом, принимаем нулевую гипотезу.





