математическая статистика_примеры и задачи
реклама

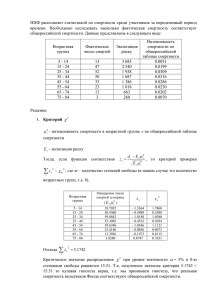
Министерство образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
ПРИМЕРЫ И ЗАДАЧИ
Утверждено Редакционно-издательским советом университета в качестве
учебного пособия
НОВОСИБИРСК
2011
УДК 519.2(075.8)
М34
Рецензенты: А. Г. Пинус, д-р физ.-мат. наук, проф.,
Т. М. Назарова, кандидат физ.-мат. наук, доц.,
Работа подготовлена на кафедре высшей математики
для студентов нематематических специальностей
М34
Математическая статистика. Примеры и задачи : учебное пособие / М. Ю. Васильчик, А. П. Ковалевский, И. М. Пупышев и др. —
Новосибирск : Изд-во НГТУ, 2011 — 84 с.
ISBN 978-5-7782-1721-8
Настоящее учебное пособие подготовлено для студентов очного и заочного отделений технических направлений и специальностей, изучающих
теорию вероятностей и математическую статистику в обычном объеме. При
его написании были использованы методические разработки и другие материалы, ранее изданные кафедрой высшей математики НГТУ. Эти материалы
включены в текст пособия без ссылок, за что мы приносим свои извинения.
Все замечания по содержанию данной работы просим передавать на кафедру высшей математики. Они будут с благодарностью приняты и учтены в
следующих изданиях.
УДК 519.2(075.8)
ISBN 978-5-7782-1721-8
c Васильчик М.Ю., Ковалевский А.П.,
Пупышев И.М., Тренева Т.В.,
Хаблов В.В., Шефель Г.С., 2011
c Новосибирский государственный
технический университет, 2011
Оглавление
Глава 1. Основы выборочного метода
§ 1.1 Выборка. Базовые понятия математической статистики.
§ 1.2 Выборочные характеристики . . . . . . . . . . . . . . . . .
§ 1.3 Точечные оценки параметров распределения . . . . . . .
§ 1.4 Интервальные оценки параметров распределения . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Глава 2. Проверка статистических гипотез.
§ 2.1 Основные сведения. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§ 2.2 Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности. . . . . . . . . . . . . . . . . . . . . . . . . .
§ 2.3 Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией нормальной совокупности. . . . . . . . . . . . . .
§ 2.4 Сравнение дисперсий двух нормальных генеральных совокупностей. . .
§ 2.5 Сравнение средних двух генеральных совокупностей. . . . . . . . . . . .
§ 2.6 Проверка гипотезы о виде распределения генеральной совокупности
по критерию
Пирсона (критерий x2 ). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.1 Проверка гипотезы о нормальном распределении генеральной совокупности по критерию . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.2 Проверка гипотезы о равномерном распределении генеральной совокупности. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.6.3 Проверка гипотезы о распределении генеральной совокупности по
закону Пуассона. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава 3. Метод наименьших квадратов и элементы регрессионного анализа.
§ 3.1 Предварительные сведения. Метод
наименьших квадратов. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§ 3.2 Проверка гипотезы о значимости выборочного коэффициента корреляции. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§ 3.3 Уравнения линейной регрессии. . . . . . . . . . . . . . . . . . . . . . . . . .
ПРИЛОЖЕНИЕ. Таблицы
4
4
8
10
14
21
21
24
28
31
33
37
37
40
42
46
46
48
55
i
Литература
xxiv
3
Глава 1
Основы выборочного метода
1.1 Выборка. Базовые понятия математической статистики.
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ. X,Y, . . . — имена случайных величин, чьи законы распределения неизвестны (или известны лишь частично) и подлежат
исследованию. Если X — такая случайная величина, то ее в математической
статистике называют генеральной совокупностью. Для исследования производят n независимых наблюдений, в которых получают значения
→
-X = (X1 , X2 , . . . , Xn ) — выборку объема n из генеральной совокупности.
Если элементы выборки упорядочить:
X(1) , X(2) , . . . , X(n) ), (X(1) à X(2) à . . . à X(n) , то результат называют
вариационным рядом. Число X(n) − X(1) называется размахом выборки.
Аналогом функции распределения в статистике является выборочная,
или эмпирическая функция распределения: F ∗ (x) =
nx
, где nx — число элеn
ментов выборки, меньших, чем x. График F ∗ (x) имеет вид, как на рис.1
Если обозначить nk — количество элементов выборки, равное Xk , то
nk
— относительные частоты наблюдаечисла nk — частоты, а wk =
n
мых значений. Если nk имеет (локально) максимальное значение, то соот→
-ветствующее Xk называют модой выборки X .
→
--
1.1. Для выборки X = (5, 1, −2, 10, 1, 5, 5, 3, 5, 6) построить вариационный ряд и определить моды.
4
F∗ 1
2/n
1/n
X(1) O
X(3)
X(2)
x
X(n)
Рис. 1
РЕШЕНИЕ. Вариационный ряд
X(1) , X(2) , . . . , X(10) = (−2, 1, 1, 3, 5, 5, 5, 5, 6, 10) .
Модами являются значения 1 и 5. Размах выборки равен 12.
Выборочный ряд распределения — это такое представление вариационного ряда:
X
w
X(1)
w1
X(2)
w2
...
...
1.1 (Продолжение). Для примера, приведенного выше, построить выборочный ряд и график выборочной функции распределения.
X −2 1
3
5
6
10
РЕШЕНИЕ.
w 0, 1 0, 2 0, 1 0, 4 0, 1 0, 1
Эмпирическая функция распределения приведена на рис.2
1
0, 9
0, 8
F ∗ (x)
0, 4
0, 3
0, 1
−2
O
1
3
5 6
Рис. 2
5
10
x
Аналогом плотности распределения в статистике является гистограмма. Для любого набора чисел x0 , x2 , . . . , xr если x0 à X(1) и X(n) à xr ,
тоnопределены значения n1 ,n2 ,. . .,nr , где nk — число значений в выборке,
попавших в промежуток Dk = [xk−1 , xk ), k = 1, 2, . . . , r − 1. Последний
промежуток Dr , делаем замкнутым: Dr = [xr −1 , xr ]. Числа nk это частоты
попадания элементов выборки в промежуток Dk . По определению функция
n
f ∗ (x) принимает на промежутке Dk постоянное значение, равное k , где
nhk
hk = xk − xk−1 — длина промежутка Dk . Часто длину hk выбирают постоянной hk = h, а число промежутков r определяют по формуле Стеджеса :
r = log2 n + 1.
xr − x1
. Вне проЗдесь [. . .] — целая часть числа. При этом выборе h =
r
∗
межутка [x0 , xr ] значение функции f (x) полагают равным нулю. Так построенная функция f ∗ (x) называется гистограммой. Ее графиком является ступенчатая фигура. Суммарная площадь под всеми ступеньками всегда
равна
n1
n2
n1 n2
n
· h1 +
· h2 + . . . =
+
+ . . . = = 1.
nh1
nh2
n
n
n
f ∗ (x)
nr
nhr
n2
nh2
n1
nh1
x0
O
x1
xr
x
Рис. 3
1.1 (Продолжение). Для рассматриваемого примера построить гистограмму.
РЕШЕНИЕ. r = [log2 n] + 1 = [log2 10] + 1 = 4. При выборе x0 = −2 и
x4 = 10 получаем: h = 3, n1 = 1, n2 = 3, n3 = 5, n4 = 1.
6
f ∗ (x)
5/30
3/30
1/30
−2
4
1
O
7
10
x
Рис. 4
Другое приближение плотности распределения с помощью выборки —
полигон частот. Это — ломаная, соединяющая середины верхних оснований прямоугольников, образующих гистограмму. Звенья ломаной спроектированы на отрезки одинаковой длины и площадь под графиком полигона
равна единице.
5/30
f ∗ (x)
3/30
1/30
−2
O
1
4
7
Рис. 5
10
x
Гистограммой частот называется гистограмма, умноженная на объем
выборки n. В этом случае суммарная площадь под всеми ступеньками равна
n2
n1
·h +
· h + . . . = n1 + n2 + . . . = n.
h1 1 h2 2
1.2 По выборке объема n = 100 построена гистограмма частот:
7
y
) 18
z
12
8
4
O
2
4
6
x
8
Рис. 6
Чему равно значение z ?
РЕШЕНИЕ. Вычисляя площадь под ступеньками, приходим к равенству 68+
2z = 100, откуда z = 16.
1.2
Выборочные характеристики
Для выборочного ряда распределения
X
nk
Число X =
1
n
X(1)
n1
X(2)
n2
...
...
n
X(1) · n1 + X(2) · n2 + . . . =
1X
n k= 1
Xk называется выбороч-
ным средним.
1.1 (Продолжение). Найти выборочное среднее для нашего примера.
X −2 1 3 5 6 10
РЕШЕНИЕ.
nk 1
2 1 4 1 1
X = −2 · 1 + 1 · 2 + . . . + 10 · 1 = 3, 9 .
Число S2X = S2 = Dв X =
n
2
2
2
1 1X
=
n
X(1) − X
· n1 + X(2) − X
· n2 + . . .
p
=
n l =1
Xl − X
на-
зывают выборочной дисперсией; S = sв X = Dв X — выборочное среднее
квадратическое отклонение. В случае, когда числа Xn целые, а X — нет,
8
более удобной для устного счета является формула
2
Dв X = X 2 − X =
n
1 2
2
1X 2
2
X(1) · n1 + X(22) · n2 + . . . − X =
X −X
10
n l =1 l
1.1 (Продолжение). Для текущего примера найти выборочную дисперсию.
РЕШЕНИЕ.
1
2
Dв X =
(−2) · 1 + 12 · 2 + 32 · 1 + 52 · 4 + 62 · 1 + 102 · 1 − 3, 92 =
10
p
= 8, 369; sв X = 8, 369 ≈ 2, 892 9.
n
1X k
Xl назыДля любого натурального значения k число mk = X k =
n l =1
вается k-м выборочным моментом.
Свойства выборочных математического ожидания и дисперсии.
1. Если X = C — постоянная, то X = C.
2. Если C — постоянная, то CX = CX.
3. Если X = C — постоянная, то Dв X = 0.
4. Если C — постоянная, то Dв X + C = Dв X.
5. Если C — постоянная, то Dв CX = C2 Dв X.
1.3 Найти выборочные среднее и среднее квадратическое отклонение
X 123, 4 128, 4 133, 4
.
для вариационного ряда
nk 4
1
5
РЕШЕНИЕ. Заметим, что значения в выборке следуют друг за другом с шагом h = 5. Это позволяет представить X в виде X = 5 · Y + 128, 4. ВаY −1 0 1
. Для Y выборочные
риационный ряд для Y имеет вид
n 4
1 5
характеристики вычисляются легко:
2
Y = 0, 1 . SY2 = Y 2 − Y = 0, 9 − 0, 01 = 0, 89 . По свойствам 1–5
Dв (5 · Y + 128, 4) =
X = 5 · Y + 128, 4 = 5 · Y + 128, 4 = 128, 9. S2X = p
Dв (5 · Y ) = 25 · SY2 = 22, 25 . Отсюда sвY = SY = 22, 25 ≈ 4, 717 .
Задачи для самостоятельного решения.
→
-1.4 Дана выборка X = (4, 0, 9, 0, 4, −3, 2, 4, 5, 4) из генеральной совокупности. Произвести необходимые вычисления и
1) построить вариационный ряд;
2) определить моды выборки;
9
3) по формуле Стеджеса найти число интервалов для построения гистограммы и построить ее;
4) найти выборочные: среднее, дисперсию, исправленную дисперсию;
5) построить график выборочной функции распределения.
1.5 Выполнить задания предыдущей задачи для выборки
→
-X = (11, 2, 6, 7, 6, −1, 4, 6, 2, 6).
1.6 Найти выборочные среднее и среднее квадратическое отклонение для
X 131, 7 136, 7 141, 7
.
выборочного ряда
nk 3
2
5
1.3
Точечные оценки параметров распределения
Пусть распределение генеральной совокупности известно частично, например его функция распределения содержит один или несколько неизвестных параметров q = (q1 , q2 , . . .) Для определения этих параметров используют статистики. Статистика — это функция, значения q∗ которой
→
-зависят от выборки X и которая
используется для (приближенного)
на→
-- →
-- ∗
∗
хождения значения q ≈ q X . Такие функции q X называются точечными оценками параметров q. Например, часто используется оценка
a ≈ X для неизвестного математического ожидания M(X ) = a генеральной совокупности X . Для оценки дисперсии s2 можно использовать
статистику Dв X = S2 . Важнейшим для анализа является следующее соображение: каждое значение Xi можно рассматривать как значение случайной величины, имеющей то же распределение, что и генеральная совокупность X , и случайныевеличины
Xi и X j независимы при i ≠ j. То
→
--
гда любая статистика q∗ X — случайная величина, закон распределения
которой определяется
законом распределения
генеральной совокупности.
→
→
-- -- ∗
∗
= q, то оценка q X называется несмещенной. НаЕсли M q X
1
пример, M X = M
n
X
n
1X
n
M (Xl ) =
1X
M (X ) = M (X ) .
n l =1
Таким образом X — несмещенная оценка математического ожидания a =
n−1 2
M (X ) . Можно показать, что M S2 =
s . Поэтому оценка S2 —
n
смещенная оценка параметра s2 = D(x). Несмещенной является оценка
n 2
S.
S20 =
n−1
n l =1
Xl =
n l =1
Методы получения оценок параметров распределения.
10
Из всех методов рассмотрим два.
I. Метод моментов. Он основан на требовании равенств: для q = q∗
mk = X k ,
где X k — k-й выборочный момент, а mk = M X k — момент k-го порядка
генеральной совокупности.
Получение оценки методом моментов складывается из следующих трех
этапов:
1. Записать (или вычислить) выражение
mk = mk (q) = M X k .
2. Выразить q через M X k .
3. Заменить q на q∗ , а M X k на X k .
1.7 Известно, что X ⊂
= N a, s2 . Найти оценки параметров распределения a, s2 по методу моментов.
РЕШЕНИЕ. Параметров распределения — два. Выпишем два уравнения
для этих двух неизвестных:
1)
2)
m1 a, s2 = M(X ) = a;
m2 a, s2 = M(X 2 ) = M X 2 2 + D(X ) = a2 + s2 .
a = M(X );
3)
s2 = M X 2 − M X 2 2 .
a∗ = X ;
s2 ∗ = X 2 − X 2 = DВ (X ).
II. Метод максимального правдоподобия. Он основан на том соображе→
-нии, что если была реализована выборка X, то пара метр q должен быть
та →
-- ким, чтобы вероятность этого события была максимальной. Если P q, X
— эта вероятность, то по необходимому условию экстремума производная
этой функции по переменным q есть ноль. Если q = (q1 , q2 , . . .), то все
11
→
-- ∂P q, X
→
-- = 0. Функция P q, X называется функ∂qi
→
-цией правдоподобия, соответствующей выборке X. По теореме умноже →
-- n
→
∂P q, X
-- Y
ния вероятностей P q, X = P (q, Xl ) . Вместо уравнений
=
∂qi
l =1
частные производные
0 технически более удобными являются равносильные уравнения
→
-- ∂ ln P q, X
∂qi
= 0,
i = 1, 2, . . .
Систему этих уравнений
и решают для определения параметровраспреде→
-- →
-- ∗
ления. Если q X — решение этой системы, то говорят, что q∗ X — это
оценки параметров распределения q, полученные по методу максимального правдоподобия.
Изложенное выше справедливо для случая дискретного распределения
генеральной совокупности X . Аналогично для распределения, имеющего
плотность f (q, x), функцией правдоподобия, соответствующей выборке
→
--
→
-- X , называют P q, X =
n
Y
f (q, Xl ) и для определения параметров рас-
l =1
пределения решают ту же систему уравнений
→
-- ∂ ln P q, X
∂qi
→
-- = 0,
i = 1, 2, . . .
Решение этой системы q∗ X — это оценки параметров распределения q,
полученные по методу максимального правдоподобия.
1.8 Известно, что закон распределения генеральной совокупности X име-
X
P
x1 x2
, где x1 и x2 — известные числа. Требуется опредеp 1− p
лить параметр p по методу максимального правдоподобия.
→
-РЕШЕНИЕ. Пусть в выборке X содержится m значений x1 , остальные n −
m — значения x2 . Тогда
ет вид
→
-- P q, X =
m) ln(1 − p).
n
Y
l =1
→
-- P p, Xl = pm (1 − p)n−m . ln P q, X = m ln p + (n −
→
-- ∂ ln P p, X
m n−m
= 0 равносильно
−
= 0, или m = np,
p
1− p
→
-m
m
откуда p =
. Таким образом, p∗ X =
— оценка максимального
Уравнение
∂p
n
n
правдоподобия параметра p.
12
1.9 Произведена
выборка объема n из генеральной совокупности X ⊂
=
N a, s2 . Построить оценки параметров a, s2 по методу максимального
правдоподобия.
РЕШЕНИЕ. Вычислим функцию правдоподобия
→
-- P a, s, X =
n
Y
l =1
f (a, s, Xl ) =
n
Y
1
√
s 2p
l =1
e
−
(Xl − a)
2s2
2
.
Определим значения параметров, при которых эта функция, или, что равносильно, функция
n
2
X
→
-- 1
1
(Xl − a)
= − ln(2p) − n ln s −
ln P a, s, X = − ln(2p) − n ln s −
2
2
2s
2
l =1
n 2
X − 2aX + a2 . Если паре (a, s) соответствует максимум этой функ2
2s
ции, то
→
--
∂
ln
P
a,
s
,
X
= 0;
∂a
→
∂ ln P a, s, X
= 0;
∂s
X − a = 0;
1 − 1 X 2 − a2 = 0.
3
или
s
s
Окончательный
вид оценки максимального правдоподобия:
a∗ = X ;
Заметим, что для нормального распре
2
2 ∗
s
= X 2 − X = Dв X.
деления эти оценки совпали с полученными по методу моментов.
Задачи для самостоятельного решения.
1.10 Применить метод моментов и найти оценку q для равномерного распределения X ⊂
= U (0, q) .
1.11 Применить метод моментов и найти оценки q1 , q2 для равномерного
распределения X ⊂
= U (q1 , q2 ) .
1.12 Применить метод моментов и(найти оценку q для показательного расqe−qx , x á 0;
пределения с плотностью f (x) =
0, x < 0.
→
--
1.13 Для выборки X ⊂
= P(q) применить метод моментов и найти оценку q.
(Распределение Пуассона: pn = e−q ·
→
--
qn
,
n!
n = 0, 1, 2, . . .)
1.14 Для выборки X ⊂
= N(q, 1) применить метод моментов и найти оценку
q.
13
→
--
1.15 Для выборки X ⊂
= N(0, q) применить метод моментов и найти оценку
q.
1.16 Применить метод максимального правдоподобия и найти оценку q для
равномерного распределения X ⊂
= U (0, q) .
1.17 Применить метод максимального правдоподобия и найти оценки q1, q2
для равномерного распределения X ⊂
= U (q1 , q2 ) .
1.18 Применить метод максимального правдоподобия и найти оценку q для
показательного
распределения с плотностью
(
qe−qx , x á 0;
f (x) =
0, x < 0.
→
--
1.19 Для выборки X ⊂
= P(q) применить метод максимального правдопо-
добия и найти оценку q. (Распределение Пуассона: pn = e−q ·
qn
,
n!
n=
0, 1, 2, . . .)
→
-1.20 Для выборки X ⊂
= N(q, 1) применить метод максимального правдоподобия и найти оценку q.
→
-1.21 Для выборки X ⊂
= N(0, q) применить метод максимального правдоподобия и найти оценку q.
1.4
Интервальные оценки параметров распределения
Пусть распределение генеральной совокупности содержит неизвестный
→
-параметр q. Говорят, что построенный по выборке X объема n интервал
(q− , q+ ) накрывает параметр q с надежностью g, если вероятность события q ∈ (q− , q+ ) стремится к g при стремлении n к бесконечности. В
этом случае интервал (q− , q+ ) называют доверительным интервалом для
q; построение такого интервала — получение интервальной оценки для q;
число g ∈ (0, 1) — доверительная вероятность, или уровень доверия оценки; числа q− и q+ — нижняя и верхняя доверительные границы.
В случае, когда при любом n вероятность P (q ∈ (q− , q+ )) = g, доверительный интервал называют точным.
Рассмотрим несколько случаев построения доверительного интервала
для параметров нормально распределенной генеральной совокупности. В
рассуждениях будем опираться на лемму Фишера:
Если произведена выборка объема n из X ⊂
= N a, s2 , и Y = a − X , то
14
√
Y n
1)
⊂
= N(0, 1);
s
2) случайная величина
n
1 X
s2
n =1
2
(Xn − a) = x2n , то есть имеет распределе-
ние, называемое «хи-квадрат с n степенями свободы»;
3)
nS2
= x2n−1 ;
s2
√
Y n−1
4)
⊂
= Tn−1 , то есть имеет распределение, которое называется
S
распределением Стьюдента с n − 1 степенями свободы.
Заметим, что распределения Хи-квадрат и Стюдента «известны», то есть
хорошо изучены, значения их функций распределения составлены в подробные таблицы и могут быть вычислены с практически любой наперед заданной точностью.
Примеры.
1. X имеет нормальный закон распределения: X ⊂
= N a, s2 , значение
параметра s известно, значением g задаёмся, а для a строим доверительный
интервал, который указывает на положение a на числовой оси по возможности наиболее точно, то есть имеет наименьшую длину.
При построении доверительных интервалов последнее требование не всегда удаётся выполнить, но в рассматриваемом случае помогают геометриa − X ∈
ческие соображения. Вероятность
√ (a− , a+ ) ⇐⇒ √
√
события a ∈
n n
Y n
a− − X ·
∈
, a+ − X ·
. Слуa− − X, a+ − X ⇐⇒
s
s
s
√
Y n
чайная величина
по лемме Фишера имеет стандартное нормальное
s
распределение,
и вероятность
события √ √
√ Y n
∈
s
a− − X ·
са над интервалом
n
n
, a+ − X ·
равна площади под кривой Гаусs
s
√
√ n n
, a+ − X ·
.
a− − X ·
s
s
Длина промежутка (a− , a+ ) или, что равносильно
√n √n a− − X ·
, a+ − X ·
S0
S0
для заданной площади g будет наименьшей, если этот промежуток симметричен относительно нуля: a+ − X = d; a− − X = −d.
15
fY
y
x
−d
2d
3d
Число d, точность оценки, отвечает равенству P(−d < Y < d) = g ⇔
P −
√
d
O
Рис. 7
√
√
√ d n Y n d n
<
<
s
s
s
= g ⇔ 2F0
√ d n
= g . Если обозначить
s
s
d n
= t , то точность оценки d = t √ , и
s
n
√
√ √
d n Y n d n
<
<
=g=
P −
s
s s
= P(−d < a − X < d) = P X − d < a < X + d .
Таким образом, X − d, X + d — искомый доверительный интервал для
математического ожидания a.
1.22 Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания a нормально распределенной генеральной совокупности, если даны генеральное среднее квадратическое отклонение s = 5 и выборочное среднее X = 13. Объем выборки 16.
√ РЕШЕНИЕ. Найдем точность оценки d из уравнения 2F0
d n
= g, что
s
4d
4d
=
= 0, 475. Из таблицы 4 Приложения имеем:
5
5
1, 96 или d = 2, 45. Доверительный
интервал
X − d < a < X + d =(10, 55; 15, 45).
равносильно F0
2. X имеет нормальный закон распределения: X ⊂
= N a, s2 , значение параметра s НЕизвестно, значением g задаёмся, а для a строим доверительный интервал, который указывает на положение a на числовой оси
по возможности наиболее точно, то есть имеет наименьшую длину.
В рассматриваемом случае будем рассуждать аналогично тому, как рассуждали в предыдущем примере. Вероятность события
a ∈ (a− , a+ ) ⇐⇒ a − X ∈ a− − X, a+ − X ⇐⇒
16
√
√
√
!
n−1 n−1
Y n−1
a− − X ·
∈
, a+ − X ·
.
⇐⇒
S
S
S
√
Y n−1
Случайная величина
по лемме Фишера имеет распределение СтюS
дента с n − 1 степенями свободы. Вероятность события
!
√
√n − 1 √n − 1
Y n−1
a− − X ·
∈
, a+ − X ·
S
S
S
равна площади под графиком плотности распределения Стюдента над интервалом
!
√n − 1 √n − 1
a− − X ·
, a+ − X ·
S
Длина промежутка (a− , a+ ) или, что равносильно
√
.
S
√ n n
a− − X ·
, a+ − X ·
S0
S0
для заданной площади g будет наименьшей (как и для нормального закона),
если промежуток
√
√
!
n−1 n−1
a− − X ·
, a+ − X ·
S
S
симметричен относительно нуля: a+ − X = d; a− − X = −d.
Число d — точность оценки — отвечает равенству
!
√
√
√
n−1 Y n−1
n−1
P(−d < Y < d) = g ⇔ P −d ·
<
<d·
=
S
S
S
= g ⇔ FT
√
d n−1
S
!
=
1−g
.
2
В этом равенстве FT — функция распределения
распределения Стьюдента,
√
d n−1
а FT = 1 − FT . Если обозначить
= t , то точность оценки d =
S
S
,и
t√
n−1
√
√
√
!
n−1 Y n−1
n−1
P −d ·
<
< d·
=g=
S
S
S
= P(−d < a − X < d) = P X − d < a < X + d .
Таким образом, X − d, X + d — искомый доверительный интервал для
математического ожидания a.
17
1.23 Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания a нормально распределенной генеральной совокупности, если даны выборочное среднее квадратическое отклонение S = 5 и выборочное среднее X = 13. Объем выборки 17. √
!
d n−1
=
РЕШЕНИЕ. Найдем точность оценки d из уравнения FT
S
1−g
, что равносильно FT = 0, 025. Из таблицы 5 Приложения имеем:
2
4d
= 2, 12 или d = 2, 65. Доверительный интервал
5
X − d < a < X + d =(10, 35; 15, 65).
3. X имеет нормальный закон распределения: X ⊂
= N a, s2 , значение
параметров a, s2 НЕизвестны, значением g задаёмся. Построить доверительный интервал для s2 .
Отметим сразу, что как и всегда при построении доверительного интервала, если решение задачи существует, то таких решений бесконечно много.
Приведем только одну конструкцию — простую, хотя и заведомо не оптимальную в том смысле, что строящийся интервал не является самым коротким из возможных.
Для решения задачи заметим, что по лемме Фишера случайная величина
nS2
распределена как x2n−1 . Обозначим Fx2 ее функцию распределения и
s2
будем искать значения
! x1 и x2 , для которых вероятность
nS2
P x1 < 2 < x2 = g. Для однозначности потребуем, чтобы
s !
!
2
nS2
1−g
nS
2
à
x
=
P
á
x
P
(
x
)
=
=
F
1
2 = 1 − Fx2 (x2 ).
1
x
s2
2
s2
1−g
1+g
и Fx2 (x2 ) =
эти x1 и x2 найдем по
По равенствам Fx2 (x1 ) =
2
2
таблице значений функции распределения Fx2 (см. приложение). Очевидно,
что неравенство x1 <
s2− =
nS2
nS2
nS2
< s2 <
и, если
< x2 равносильно
2
s
x2
x1
nS2
nS2
, а s2+ =
, то s2− , s2+ — нужный доверительный интервал.
x2
x1
1.24 Найти доверительный интервал для оценки с надежностью 0,9 неизвестной дисперсии s2 нормально распределенной генеральной совокупности, если даны выборочная дисперсия S2 = 4 и объем выборки 10.
1−g
1+g
РЕШЕНИЕ. По равенствам Fx2 (x1 ) =
и Fx2 (x2 ) =
,
2
2
2
2
то есть Fx (x1 ) = 0, 05 и Fx (x2 ) = 0, 95 при числе степеней свободы 9 из
18
таблицы 6 Приложения найдем: x1 = 3, 33 и x2 = 16, 9. Доверительный
интервал
!
!
10 · 4 10 · 4
nS2 nS2
2
2
=
,
,
= (2, 367; 12, 012)
s− , s+ =
x2 x1
16, 9 3, 33
4. X имеет нормальный закон распределения: X ⊂
= N a, s2 , значение
параметра a известно, s2 НЕизвестно, значением g задаёмся. Построить доверительный интервал для s2 .
Этот случай отличается от предыдущего только тем, что число степеней
свободы для распределения x2 полагают равным не n − 1, а n − 2 — на единицу меньше.
Задачи для самостоятельного решения.
1.25 По выборке объема n = 25 из нормально распределенной генеральной совокупности X с дисперсией D(X ) = 25 вычисленное среднее X =
14. Построить доверительный интервал для неизвестного математического
ожидания, если требуемая надежность оценки а) g = 0, 95; б) g = 0, 9.
1.26 По выборке объема n = 16 из нормально распределенной генеральной совокупности X с дисперсией D(X ) = 25 вычисленное среднее
X = 14. Построить доверительный интервал для неизвестного математического ожидания, если требуемая надежность оценки g = 0, 95. Сравните
результат с ответом задачи 25(а).
1.27 По выборке объема n = 25 из нормально распределенной генеральной совокупности X с дисперсией D(X ) = 9 вычисленное среднее
X = 14. Построить доверительный интервал для неизвестного математического ожидания, если требуемая надежность оценки g = 0, 95. Сравните
результат с ответом задачи 25(а).
1.28 По выборке объема n = 26 из нормально распределенной генеральной совокупности X с выборочной дисперсией S2 = 25 вычисленное
среднее X = 14. Построить доверительный интервал для неизвестного математического ожидания, если требуемая надежность оценки а) g = 0, 95
(сравните результат с ответом задачи 25(а)); б) g = 0, 9.
1.29 По выборке объема n = 17 из нормально распределенной генеральной совокупности X с выборочной дисперсией S2 = 25 вычисленное среднее X = 14. Построить доверительный интервал для неизвестного математического ожидания, если требуемая надежность оценки g = 0, 95. Сравните результат с ответом задачи 28(а).
1.30 По выборке объема n = 26 из нормально распределенной генеральной совокупности X с выборочной дисперсией S2 = 9 вычисленное
среднее X = 14. Построить доверительный интервал для неизвестного математического ожидания, если требуемая надежность оценки g = 0, 95.
Сравните результат с ответом задачи 28(а).
19
1.31 По выборке объема n = 25 из нормально распределенной генеральной совокупности X вычисленное среднее X = 14. Построить доверительный интервал для неизвестного математического ожидания, если требуемая
надежность оценки g = 0, 95 и S2 = 25. Сравните результат с ответом задачи 25(а).
1.32 По выборке объема n = 26 из нормально распределенной генеральной совокупности X с выборочной дисперсией S2 = 25 построить доверительный интервал для неизвестной дисперсии, если требуемая надежность
оценки а) g = 0, 95; б) g = 0, 9.
ОТВЕТЫ.
1.25 а) (12,04;15,96); б) (12,355;15,645). 1.26 (11,55;16,45).
1.27 (12,824;15,176). 1.28 а) (11,94;16,06); б) (11,29;16,71).
1.29 (11,825;16,175). 1.30 (12,764;15,236). 1.31 (11,9;16,1).
1.32 а) (15,51;46,97); б) (16,71; 42,26).
20
Глава 2
Проверка статистических
гипотез.
2.1
Основные сведения.
Статистической гипотезой называется всякое высказывание о генеральной совокупности- изучаемой случайной величине, проверяемое по результатам наблюдений (по выборке), не располагая сведениями о всей генеральной совокупности, по определенным правилам. По выборочным данным делают вывод о том, можно принять эту гипотезу или нет. Процедура
сопоставления высказанной гипотезы с выборочными данными называется
проверкой гипотезы. Обычно гипотезы обозначаются H, H0 , H1 , ....
Гипотезы бывают простые и сложные. Простойназывается гипотеза, однозначно фиксирующая закон распределения случайной величины. В противном случае гипотеза называется сложной. Допустим, генеральная совокупность Х имеет нормальный закон распределения. Обозначим через a математическое ожидание Х, s2 - дисперсию. Предположим, что дисперсия s2
известна. Тогда гипотеза H0 : a = a0 , где a0 - фиксированное известное
число, - простая гипотеза, H0 : a > a0 (или H0 : a < a0 ) - сложная односторонняя гипотеза, H0 : a0 < a < a1 - сложная двусторонняя гипотеза. Если неизвестны и математическое ожидание и дисперсия, то гипотеза
H0 : a = a0 - сложная гипотеза, т.к. дисперсия неизвестна и, значит, закон
распределения случайной величины не фиксируется однозначно.
На первом шаге, имея выборочные данные и руководствуясь конкретными условиями рассматриваемой задачи, формулируют гипотезу H0 , которую называют нулевой(основной) и гипотезу H1 , конкурирующую с гипо21
тезой H0 . Ее часто называют альтернативнойгипотезой. По данной выборке будет принято решение - справедлива ли гипотеза H0 , или гипотеза H1 .
Необходимо отметить, что как правило в математической статистике не делается категорический вывод - "гипотеза H0 истинна или гипотеза H0 ложна. О гипотезе делается вывод - вероятность справедливости гипотезы H0
большая, чтобы ее принять, или "гипотеза H0 не отвергается или "гипотеза
H0 не противоречит выборочным данным".
На втором шаге задается вероятность a, которую называют уровнем значимости. Так как высказывание, что H0 справедлива для генеральной совокупности принимается по выборочным данным, т.е. по ограниченному
числу наблюдений, то решение может быть ошибочным. Если гипотеза H0
отвергается (т.е., принимается гипотеза H1 ), а на самом деле гипотеза H0
верна, то совершается ошибка первого рода. Уровень значимости - это вероятность ошибки первого рода, равна a. Вероятность a задается заранее малым числом. Обычно используются значения a : 0, 05; 0, 01; 0, 005; 0, 001.
Для этих значений составлены таблицы.
Если принимается гипотеза H0 , а верна конкурирующая гипотеза H1 , то
совершается ошибка второго рода. Вероятность сделать ошибку второго рода обозначается часто b. Отметим, что в результате проверки относительно
гипотезы H0 может быть принято и правильное решение. Вероятность этого решения равна 1 − a. Если не принимают гипотезу H0 (т.е. принимают
гипотезу H1 ), тогда как и на самом деле гипотеза H0 не верна, то вероятность этого решения равна 1 − b.
На третьем шаге находят величину w = w(X1 , . . . , Xn ), зависящую от
случайной выборки (X1 , . . . , Xn ).По ее значениям выносят решение о "расхождении выборки с гипотезой H0 ". Величина w(X1 , . . . , Xn ) есть случайная величина т.к. выборка X1 , . . . , Xn случайна и она подчиняется при выполнении гипотезы H0 некоторому известному закону распределения, затабулированному, т.е. для которого составлены таблицы. Величину w называют
критерием.
На четвертом шаге выделяется подобласть значений W критерия w, которые свидетельствуют о существовании расхождения выборки с гипотезой
H0 и, следовательно, о невозможности принять гипотезу H0 . Подобласть W
называется критической областью. Пусть критическая область выделена.
Тогда, если вычисленные по выборке значения w попадают в критическую
область, то гипотеза H0 отвергается и принимается гипотеза H1 . Ясно, что
такое решение может оказаться ошибочным, и на самом деле гипотеза H0
может быть справедливой. То есть, ориентируясь на критическую область
можно совершить ошибку первого рода, вероятность которой задана заранее и равна a. Отсюда вытекает требование к критической области:
— вероятность того, что критерий w примет значение из критической
22
области W , должна быть равна заданному числу a, т.е. P(w ∈ W ) = a. Критическая область равенством P(w ∈ W ) = a определяется неоднозначно.
Если y = fv (x) - плотность критерия w, то на оси абсцисс существует бесконечное число областей — интервалов, таких, что площади построенных на
них криволинейных трапеций равны a.
y
y = fv(x)
x
O
x
кр
a,пр
y
y = fv(x)
x
x
кр
a,л
O
y
y = fv(x)
x
O
x
кр
a,л
x
кр
a,пр
Поэтому выдвигается еще следующее требование: критическая область
должна быть расположена так, чтобы при заданной вероятности a вероятность b ошибки второго рода была минимальной.
Возможны три вида расположения критической области (в зависимости
от вида нулевой и конкурирующей гипотез, вида распределениякритерия w).
кр
Правосторонняя критическая область состоит из интервала xa,пр , +∞ ,
кр
кр
где xa,пр определяется из условия P w > xa,пр = a, и называется правосторонней критической точкой, отвечающей уровню значимости
a. Левокр
сторонняя критическая область состоит из интервала −∞, xa,л , где лекр
восторонняя
критическая точка xa,л определяется из условия
P w < xкр
a,л = a.
23
Двусторонняя критическая область есть объединение двух интервалов
кр
W = −∞, xкр
a/2,л
кр
xкр
a/2,пр , ∞ ,
[
где точки xa/2,л и xa/2,пр определяются из условий
P w < xкр
a/2,л =
a
, P w > xкр
a/2,пр =
a
,
2
2
и называется двусторонними критическими точками.
Последний пятый шаг состоит в том, что в формулу критерия
w = w(X1 , . . . , Xn ) вместо случайных величин подставляют конкретную
числовую выборку X1 , . . . , Xn и подсчитывают численное значение wчис
критерия. Если число wчис попадает в критическую область W , то гипотеза
H0 отвергается и принимается гипотеза H1 . Следует при этом иметь ввиду,
что можно допустить ошибку первого рода с вероятностью a.
Если wчис не попадает в критическую область, гипотеза H0 не отвергается. Это не означает, что H0 есть единственная подходящая гипотеза, просто
расхождение между выборочными данными и гипотезой H0 невелико, т.е.
гипотеза H0 не противоречит результатам наблюдений. Но наряду с H0 таким же свойством могут обладать и другие гипотезы.
2.2
Сравнение выборочной средней с гипотетической генеральной средней нормальной совокупности.
А. ДИСПЕРСИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ ИЗВЕСТНА.
Пусть генеральная совокупность Х имеет нормальный закон распределения и пусть дисперсия D(X ) = s2 известна. Имеется выборка
X1 , X2 , . . . , Xn значений величины Х. Требуется при данном уровне значимости a проверить нулевую гипотезу H0 : a = a0 , где a0 - гипотетическое
значение математического ожидания Х, при данных ниже конкурирующих
гипотезах.
1) Конкурирующая гипотеза H1 : a ≠ a0 . По выборке X1 , . . . , Xn вычисляются значения критерия
где X =
1
n
n
P
j =1
Uнабл =
√
(X − a0 ) n
s
,
(1)
X j , n− объем выборки.
По таблице для функции Лапласа находят критическую точку uкр двусторонней критической области из равенства
1−a
.
(2)
F(uкр ) =
2
24
Если | Uнабл |< uкр , то нет оснований отвергать гипотезу H0 . Если | Uнабл |>
uкр , то нулевая гипотеза H0 отвергается.
2) Конкурирующая гипотеза H1 : a > a0 . Критическая точка правосторонней критической области находится из равенства
1 − 2a
.
(3)
F(uкр
п )=
2
кр
При Uнабл < uп нет оснований отвергнуть нулевую гипотезу, при Uнабл >
uкр
п нулевая гипотеза отвергается.
3) Конкурирующая гипотеза H1 : a < a0 . По формуле (1) вычисляют
Uнабл и находят вспомогательную критическую точку uкр
п по формуле (3),
кр
кр
затем полагаем границу левосторонней критической области uл = −uп .
кр
Если Uнабл > uл , то нет оснований отвергнуть нулевую гипотезу H0 , если
Uнабл < uкр
л , то гипотеза H0 отвергается.
2.1 Из нормальной генеральной совокупности с известным средним квадратическим отклонением s = 40 извлечена выборка объема n = 64 и по
ней найдено выборочное среднее X = 136, 5.Требуется при уровне значимости a = 0, 1 проверить гипотезу H0 : a = 130 при конкурирующей
гипотезе H1 : a > 130.
РЕШЕНИЕ. Вычисляем значение критерия по формуле (1)
√
(136, 5 − 130) 64
= 1, 3.
40
По таблице для функции Лапласа находим критическую точку правосторонней критической области из равенства
1 − 2a
0, 8
F(uкр ) =
=
= 0, 4.
2
2
Получаем uкр = 1, 28. Так как Uнабл = 1, 3 > uкр , то отвергаем нулевую
гипотезу.
2.2 Из нормальной генеральной совокупности с известным средним квадратическим отклонением s = 5, 2 извлечена выборка объема n = 100 и по
ней найдено выборочное среднее X = 27, 56. Требуется при уровне значимости a = 0, 05проверить гипотезу H0 : a = 26 при конкурирующей
гипотезе H1 : a ≠ 26.
РЕШЕНИЕ. Вычисляем значение критерия (1)
Uнабл =
√
(27, 56 − 26) 100
1, 56
=
= 3.
5, 2
5, 2
По таблице для функции Лапласа находим критическую точку uкр = 1, 96.
Так как |Uнабл | = 3 > uкр = 1, 96, то нулевая гипотеза отвергается.
2.3 По паспортным данным на автодвигатель, расходы топлива на 100
км пробега составляет 10 л при среднем квадратическом отклонении 2 л. В
Uнабл =
25
результате совершенствования конструкции двигателя ожидается, что расход топлива уменьшится. Проверка 25 случайно отобранных автомобилей
с модифицированными двигателями выяснила, что средний расход топлива на 100 км пробега составляет 9,2 л. Используя 5% уровень значимости,
проверить гипотезу, что модификация повлияла на расход топлива.
2.4 По результатам n = 9 замеров установлено, что выборочное среднее время (в сек) изготовления детали X = 48. Предполагая нормальное
распределение распределение случайной величины с дисперсией s = 3 сек,
проверить при уровне значимости a = 0, 05 гипотезу H0 : a = 49 при
конкурирующей гипотезе H1 : a ≠ 49.
2.5 По выборке объема n = 16, извлеченной из нормальной генеральной
совокупности с известным средним квадратическим отклонением s = 4,
выборочным средним X , при уровне значимости a = 0, 05 проверить гипотезу H0 : a = 2 при конкурирующей гипотезе H1 : a > 2.
Б. ДИСПЕРСИЯ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ НЕИЗВЕСТНА.
В качестве критерия проверки гипотезы H0 : a = a0 принимается случайная величина
√
T=
n
1 P
X j , S20 =
1
(X − a0 ) n
n
P
S0
,
(X − X )2 . Случайная величина Т имеет
n − 1 j =1 j
распределение Стьюдента с k = n − 1 степенями свободы.
1) Для конкурирующей гипотезы H1 : a ≠ a0 по таблице критических
точек распределения Стьюдента, по заданному уровню значимости a, помещенному в верхней строке таблицы и по числу степеней свободы k = n − 1,
кр
находится критическая точка tдвукр (a, k). Для данной выборки
X1 , X2 , . . . , Xn вычисляется значение величины
√
(X − a0 ) n
.
Tнабл =
S0
кр
Если |Tнабл |< tдвукр , то нет оснований отвергнуть гипотезу H0 . Если |Tнабл |>
кр
tдвукр , то нулевая гипотеза H0 отвергается.
2). При конкурирующей гипотезе H1 : a > a0 по уровню значимости a,
где X =
n i =1
помещенному в нижней строке таблицы критических точек распределения
Стьюдента и числу степеней свободы k = n−1, находится критическая точка
кр
кр
(a, k). Как и в п.1 вычисляется значение Tнабл . Если Tнабл < tпр , то нет
tпр
кр
оснований отвергнуть гипотезу H0 . Если Tнабл > tпр , то нулевая гипотеза
отвергается.
3). При конкурирующей гипотезе H1 : a < a0 сначала находится "вспокр
кр
могательная"критическая точка (как в п.2) tпр (a, k). и полагается tл =
кр
кр
−tпр . Если Tнабл > tл , то нет оснований отвергнуть гипотезу H0 . Если Tнабл <
tлкр , то нулевая гипотеза отвергается.
26
2.6 Поставщик утверждает, что применение новой партии удобрений обеспечит урожайность пшеницы до 60 ц/га. Удобрение внесли на площади 37
га и получили
55 ц/га урожая при выборочном среднем квадратическом отклонении S0 =
3 ц/га. При 5% уровне значимости оценить справедливость утверждения поставщика.
РЕШЕНИЕ. Имеем, a0 = 60, X = 55, n = 37, S0 = 3, a = 0, 05.
Вычисляем значение критерия √
T
√
5 37
(55 − 60) 37)
=−
= −10, 138.
Tн =
3
3
кр
Вычисляем критическую точку tпр (0, 05; 36)(k = 37 − 1 = 36− число степеней свободы) по таблице критических точек распределения Стьюдента
кр
(нижняя строка): tпр (0, 05; 36) = 1, 689. Следовательно,
кр
кр
tл = −tпр = −1, 689 ∈ (−∞; −1, 689) и гипотеза H0 отвергается.
2.7 По выборке объема n = 16, извлеченной из нормальной генеральной совокупности, найдены выборочное среднее X = 118, 2 и исправленное среднее квадратическое отклонение S0 = 3, 6. Требуется при уровне
значимости a = 0, 05 проверить гипотезу H0 : a0 = 120 при конкурирующей гипотезе H1 : a ≠ 120
РЕШЕНИЕ. Вычисляем значение Tнабл √
(118, 2 − 120) 16
= −2.
Tнабл =
3, 6
По таблице критических распределения Стьюдента (верхняя строка) нахокр
дим tдвуст (0, 05; 15) (k = n − 1 = 15 - число степеней свободы). Получаем
кр
кр
= 2, 13, то нет осноtдвуст (0, 05; 15) = 2, 13.. Поскольку |Tнабл | = 2 < tдвуст
ваний отвергать гипотезу H0 .
2.8 Поставщик двигателей утверждает, что средний срок их службы равен 800 час. Для выборки из n = 17 двигателей средний срок службы оказался X = 865 час. Проверить гипотезу H0 : a0 = 800 час при уровне значимости a = 0, 01, если выборочное среднее квадратическое отклонение
S0 = 120 час и при конкурирующей гипотезе H1 :> 800.
2.9 Учет времени сборки узла машины бригадой из 10 слесарей показал,
что среднее время (в мин) сборки узла X = 76, а выборочная дисперсия
S20 = 15. Предполагая распределение времени сборки нормальной случайной величиной, проверить при уровне значимости a = 0, 01 гипотезу о том,
что a0 = 75 мин является нормативом (м.о.).
2.10 Проектный контрольный размер изделий, изготавливаемых станкомавтоматом, a0 = 35 мм. Измерено n = 20 случайно отобранных изделий и
получены следующие результаты
Xi 34,8 34,9 35,0 35,1 35,2
ni
2
3
4
6
5
27
Требуется: а) Найти выборочное среднее X и выборочное среднее квадратическое отклонение S0 . б) При уровне значимости a = 0, 05 проверить
гипотезу H0 : a = 35 мм при конкурирующей гипотезе H1 : a ≠ 35.
2.11 Дана выборка объема n = 80, извлеченная из нормально распределенной генеральной совокупности
Xi
8 8,2 8,4 8,6
ni 15 20 25 20
Требуется: а) Найти выборочное среднее X и выборочное среднеквадратическое отклонение S0 . б) При уровне значимости a = 0, 01 проверить
гипотезу H0 : a = 8 при конкурирующей гипотезе H1 : a < 8.
2.12 Дана выборка объема n = 90, извлеченная из нормально распределенной генеральной совокупности
Xi 0 1
2
3 40
ni 7 27 26 20 10
Требуется: а) Найти выборочное среднее X и выборочное среднеквадратическое отклонение S0 . б) При уровне значимости a = 0, 05 проверить
гипотезу H0 : a = 6 при конкурирующей гипотезе H1 : a > 6.
2.3
Сравнение исправленной выборочной дисперсии с гипотетической генеральной дисперсией
нормальной совокупности.
Пусть генеральная совокупность X имеет нормальное распределение,
n
1 P
Xi ,
X1 , X2 , . . . , Xn — случайная выборка. Пусть X =
2
0
S =
1
n
P
n − 1 i =1
n i =1
(Xi − X )2 . Рассматривается нулевая гипотеза H0 : s2 = s20
о равенстве неизвестной дисперсии s2 предполагаемому значению s20 при
уровне значимости a.
1) Пусть конкурирующей гипотезой будет гипотеза H1 : s2 > s20 . Критерием в этом случае служит случайная величина
x2 =
(n − 1)S20
s20
,
имеющая распределение x2 с числом степеней свободы k = n − 1. По данной
числовой выборке X1 , X2 , . . . , Xn вычисляется значение x2набл . При уровне
значимости a и данному числу степеней свободы k = n − 1 по таблице критических точек распределения x2 находится критическая точка x2кр (a, k).
28
Если x2набл < x2кр , то нет оснований отвергнуть гипотезу H0 . Если x2набл > x2кр ,
то нулевая гипотеза отвергается.
2
2) При конкурирующей
гипотезе H1 : s2 ≠
находят левую критиче
s0 . a
a
, k и правую x2пр,кр
, k . Если
2
2
2
2
2
xлев,кр < xнабл < xпр,кр , то нет оснований отвергнуть нулевую гипотезу H0 .
Если x2лев,кр > x2набл или x2пр,кр < x2набл , то нулевая гипотеза отвергается.
3) При конкурирующей гипотезе H1 : s2 < s20 . находят критическую
точку
x2кр (1 − a, k). Если x2набл > x2кр (1 − a, k), то нет оснований отвергнуть нулевую гипотезу. Если x2набл < x2кр (1 − a, k), то гипотеза H0 отвергается.
2.13 Точность работы станка-автомата проверяется по дисперсии s2 контролируемого размера изделий, которая не должна превышать 0,15. По данным из n = 25 отобранных изделий вычислена оценка дисперсии S20 =
0, 25. При уровне значимости a = 0, 01 выяснить, обеспечивает ли станок
требуемую точность.
РЕШЕНИЕ. Нулевой гипотезой будет H0 : s2 = 0, 15, конкурирующей —
гипотеза H1 : s2 > 0, 15. Вычислим значение критерия
скую точку x2лев,кр 1 −
x2 =
(n − 1)S20
s20
=
24 · 0, 25
= 40.
0, 15
По таблице критических точек распределения x2 со степенями свободы k =
24 при уровне значимости a = 0, 01,находим x2кр (0, 01; 24) = 43. Поскольку x2набл < x2кр , то нет оснований отвергнуть гипотезу H0 .
2.14 Из нормальной генеральной совокупности извлечена выборка объема n = 31 :
Xi 10,1 10,3 10,5 10,7 10,9
ni
2
7
10
9
3
Требуется: а) Найти выборочное среднее отклонение S0 . б) При уровне
значимости a = 0, 05 проверить нулевую гипотезу H0 : s2 = s20 = 0, 18,
приняв в качестве конкурирующей гипотезу H1 : s2 > 0, 18.
Xi − 10, 5
и составим
РЕШЕНИЕ. а) Перейдем к новым вариантам ui =
0, 2
расчетную таблицу
ui
ni
ui ni
-2
-1
0
1
2
2
7
10
9
3
-4
-7
0
9
6
u2i ni
8
7
0
9
24
29
4
48
= 0, 129; u2 =
=
31
31
31 · 0, 22
n
n · 0, 22 2
1 P
u − u2 =
(Xi − X )2 =
1, 548; S20 =
(1, 548 −
n − 1 i =1
n−1
30
(0, 129)2 ) = 0, 063.
б) Вычисляем значение критерия
30 · 0, 063
= 10, 5.
x2набл =
0, 18
По таблице критических точек распределения x2 при k = 30 степеней свободы иуровне значимости
a = 0, 05 находим
Результаты вычислений дают следующее: u =
x2лев,кр 1 −
a
a
, k = x2кр (0, 975; 30) = 16, 8; x2пр,кр
, k = x2кр (0, 025; 30) =
2
2
47, 0. Поскольку x2набл = 10, 5 ∉ (16, 8; 47, 0), то гипотеза H0 отвергается.
2.15 При применении определенной процедуры проверка коэффициентов трения шины по мокрому асфальту установлено, дисперсия результатов
измерения этого коэффициента составляет 0,1. Выборочное значение дисперсии, вычисленное по n = 25 результатам измерений коэффициента трения, оказалось равным 0,20. Проверить гипотезу H0 : s2 = 0, 1 при уровне
значимости a = 0, 1 и при конкурирующей гипотезе H1 : s2 ≠ 0, 1.
2.16 Из нормальной генеральной совокупности извлечена выборка объема n = 21 и по ней найдена исправленная выборочная дисперсия S20 =
16, 2. Требуется при уровне значимости a = 0, 01 проверить гипотезу H0 :
s2 = s20 = 15 при конкурирующей гипотезе H1 : s2 < 15.
2.17 В результате длительного хронометража времени сборки узла разными сбощиками установлено, что дисперсия этого времени s20 = 2мин2 .
Результаты n = 20 наблюдений за работой новичка таковы:
время сборки узла в мин Xi 56 58 60 62 64
частота ni
1
4
10
3
2
Можно ли при уровне значимости a = 0, 05 считать, что новичок работает ритмично (в том смысле, что дисперсия затрачиваемого им времени
существенно не отличается от времени остальных сборщиков)?
{УКАЗАНИЕ. Нулевая гипотеза H0 : s2 = s20 = 2, конкурирующая гипотеза
X − 60
и вычислить
H1 : s2 ≠ s20 . Перейти к условным вариантам ui = i
2
S20 .}
30
2.4
Сравнение дисперсий двух нормальных генеральных совокупностей.
По независимым выборкам, объемы которых n1 и n2 , извлеченных из
нормальных генеральных совокупностей X и Y , найдены исправленные выборочные дисперсии S20X и S20Y . Требуется сравнить дисперсии генеральных совокупностей X и Y . В качестве нулевой берется гипотеза H0 : D(X ) =
D(Y ).
1) При конкурирующей гипотезе H1 : D(X ) > D(Y ) надо по числовой
выборке X1 , X2 , . . . , Xn вычислить наблюдаемое значение критерия
Fнабл =
S20Б
,
S20М
где в числителе стоит большая из исправленных выборочных дисперсий.
По таблице критических точек распределения Фишера-Снедекора, при
заданных уровне значимости a и числе степеней свободы k1 = n1 − 1, k2 =
n2 − 1, находится критическая точка Fкр (a, k1 , k2 ). Здесь k1 - число степеней свободы большей из исправленных выборочных дисперсий S20X и S20Y .
Если Fнабл > Fкр ,то нулевая гипотеза отвергается.
2) При конкурирующей
гипотезе
H1 : D(X ) ≠ D(Y ) находим крити
ческую точку Fкр
a
a
и числам степеней
2
свободы k1 и k2 ( k1 - число степеней свободы большей дисперсии). Если
Fнабл < Fкр , то нет оснований отвергать гипотезу H0 . Если Fнабл > Fкр , то
нулевая гипотеза отвергается.
2.18 По двум независимым выборкам, объемы которых n1 = 9 и n2 = 16,
извлеченным из нормальных генеральных совокупностей X и Y , найдены
исправленные выборочные дисперсии S20X = 34, 02, S20Y = 12, 15. При
уровне значимости a = 0, 01, проверить нулевую гипотезу H0 : D(X ) =
D(Y ) при конкурирующей гипотезе H0 : D(X ) > D(Y ).
РЕШЕНИЕ. Вычисляем наблюдаемое значение критерия. Поскольку S20X >
34, 02
S20Y , то Fнабл =
= 2, 83. Число степеней свободы для X равняет12, 15
ся k1 = 8, для Y равняется k2 = 15. По таблице критических точек распределения Фишера - Снедекора находим Fкр (0, 01; 8, 15) = 4, 00. Так как
Fнабл = 2, 83 < Fкр = 4, 00 то нет основания отвергать нулевую гипотезу.
2.19 На двух станках производят одну и ту же продукцию, контролируя по
наружному диаметру изделия. Из продукции станка А было отобрано n1 =
10 изделий, а из продукции станка В n2 = 13 изделий. Выборочная оценка среднего и исправленная дисперсия для станка А равны X A = 37, 5 мм
S20A = 1, 21мм2 , для станка В - X B = 38, 6мм, S20B = 1, 44мм2 . Проверить
2
, k1 , k2 по уровню значимости
31
при уровне значимости a = 0, 1 гипотезу о равенстве дисперсий при конкурирующей гипотезе H1 : s2A ≠ s2B .
РЕШЕНИЕ. Нулевая гипотеза имеет вид H0 : s2A = s2B . Так как S20B > S20A ,
то k1 = 12, k2 = 9. Вычислим наблюдаемое значение критерия Fнабл =
1, 44
= 1, 19. По таблице критических точек распределения Фишера-Сне1, 21
декора находим Fкр
a
; k1 , k2 = Fкр (0, 05; 12, 9) = 5, 11. Так как Fнабл =
2
1, 19 < Fкр = 5, 11, то нет оснований отвергнуть нулевую гипотезу.
2.20 Расходы сырья Xi и Y j на единицу продукции по старой и новой
технологиям приведены в таблице (Xi расход сырья по старой технологии,
Y j - по новой технологии, ni - число изделий по старой технологии, Y j - по
новой.
по старой технологии
по новой технологии
Xi 304 307 308 Y j 303 304 306 308
ni
1
4
4
mj 2
6
4
1
2
при
При уровне значимости a = 0, 1 проверить гипотезу H0 : s2X = sY
2
2
конкурирующей гипотезе H1 : sX ≠ sY .
РЕШЕНИЕ. Вычислим выборочные средние и выборочные исправленные
3
3
P
1 P
1
дисперсии X =
Xi ni = 307, 11, S20X =
(X − X )2 =
nX i=1
nX − 1 j =1 i
4
1
1 P
Y m = 304, 77, S20Y =
(Y − Y )2 = 2, 1923.
1, 61, Y =
nY j =1 j j
nY − 1 j
Вычислим наблюдаемое значение критерия
Fнабл =
2, 1923
= 1, 3617.
1, 61
a
= 0, 05. Тогда Fкр (0, 05; 12, 8) =
2
= 3, 28, то нет оснований отвергнуть
У нас k1 = 13 − 1 = 12, k2 = 9 − 1 = 8,
3, 28. Так как Fнабл = 1, 3617 < Fкр
нулевую гипотезу.
2.21 По двум независимым выборкам объемов nX = 21, nY = 16, извлеченным из нормальных генеральных совокупностей X и Y , найдены ис2
= 2, 4. При уровне знаправденные выборочные дисперсии s2X = 3, 6, sY
чимости a = 0, 05 проверить гипотезу H0 : D(X ) = D(Y ) при конкурирующей гипотезе H0 : D(X ) < D(Y ).
2.22 Срок хранения продукции, изготовленной по технологии А, составил
срок хранения Xi
5 6 7
число ед. продукции ni 2 4 6
а изготовленной по технологии В:
32
срок хранения Y j
5 6 7 8
число ед. продукции m j
1 8 7 1
Предполагая, что генеральные совокупности X и Y распределены по
нормальному закону, проверить гипотезу H0 : s2A = s2B при уровне значимости a = 0, 1 и конкурирующей гипотезе H0 : s2A ≠ s2B .
2.23 При уровне значимости a = 0, 01 проверить гипотезу о равенстве
дисперсий двух нормальных генеральных совокупностях X и Y на основании данных в таблице при конкурирующих гипотезах:
2
а) H1 : s2X > sY
,
совокупность Х
совокупность Y
Xi 15 17 20 21 Y j 20 22 23 25 26
ni
2
3
2
5
mj 4
2
2
3
1
2
b) H1 : s2X > sY
,
совокупность Х
совокупность Y
Xi 304 307 308 Y j 303 304 306 308
ni
1
4
4
mj 2
6
4
1
2.5
Сравнение средних двух генеральных совокупностей.
А. ДИСПЕРСИИ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ ИЗВЕСТНЫ.
Пусть X и Y - две генеральные совокупности объема n и m соответственно, причем, либо X и Y имеют нормальное распределение, либо выборки имеют достаточно большой объем (n > 30, m > 30). В последнем
случае генеральные совокупности X и Y можно считать нормально распределенными с параметрами (X, D(X )) и (Y, D(Y )), где X и Y - выборочные средние X и Y соответственно. Рассматривается нулевая гипотеза
H0 : M(X ) = M(Y )при уровне значимости a.
1) Пусть H1 : M(X ) ≠ M(Y ) - конкурирующая гипотеза. Сначала вычисляется наблюдаемое значение критерия
X −Y
.
D(X ) D(Y )
+
n
m
по выборкам (X1 , . . . , Xn ), (Y1 , . . . ,Ym ). Затем по таблице для функции
1−a
.
Лапласа F находится критическая точка zкр из равенства F(zкр ) =
2
Если |Zнабл | < zкр ,то нет оснований отвергать гипотезу H0 . Если |Zнабл | >
zкр , то нулевая гипотеза отвергается.
Zнабл = s
33
2) Пусть конкурирующая гипотеза есть H1 : M(X ) > M(Y ). Тогда критическая точка zкр находится по таблице критических точек функции Ла1 − 2a
.
пласа F из равенства F(zкр ) =
2
Если Zнабл < zкр , то нет оснований отвергнуть гипотезу H0 . Если Zнабл >
zкр , то нулевая гипотеза отвергается.
3) Пусть конкурирующая гипотеза есть H1 : M(X ) < M(Y ). Критическая точка zкр находится так же, как и в п.2. Если Zнабл > −zкр , то нет
оснований отвергнуть гипотезу H0 . Если Zнабл < −zкр , то нулевая гипотеза
отвергается.
2.24 По выборкам объемов n = 14, m = 9 найдены средние размеры
деталей X = 182мм, Y = 185мм, соответственно, изготовленных на первом
и втором автоматах. Установлено, что размеры деталей имеют нормальный
2
= 7для первозакон распределения и известны дисперсии s2X = 5, sY
го и второго автоматов соответственно. При уровне значимости a = 0, 05
выявить влияние на средний размер деталей автомата, на котором она изготовлена. Рассмотреть два случая:
а) нулевая гипотеза H0 : M(X ) = M(Y ), конкурирующая гипотеза H1 :
M(X ) ≠ M(Y ). б) нулевая гипотеза H0 : M(X ) = M(Y ), конкурирующая гипотеза H1 : M(X ) < M(Y ).
РЕШЕНИЕ. Вычисляем наблюдаемое значение критерия
Zнабл = s
X −Y
182 − 185
= s
= −2, 816.
2
2
5
7
sX sY
+
+
14 9
n
m
a) По таблице для функции Лапласа находим критическую точку
0, 95
1−a
=
= 0, 475, zкр = 1, 96. Поскольку |Zнабл | =
F(zкр ) =
2
2
2, 816 > zкр = 1, 96, то нулевая гипотеза отвергается.
b) По таблице для функции Лапласа находим критическую точку
1 − 2a
1 − 0, 1
F(zкр ) =
=
= 0, 45, zкр = 1, 64. Так как Zнабл = −2, 816 <
2
2
zкр = −1, 64, то нулевая гипотеза отвергается.
2.25 Фирма предлагает автоматы по разливу напитков. При выборке объема n = 16 найдена средняя величина X = 182г дозы, налитой в стакан
первым автоматом. По выборке m = 9 найдена средняя величина Y = 185г
дозы, налитой в стакан вторым автоматом. По утверждению изготовителя,
случайная величина наливаемой дозы имеет нормальный закон распределения с дисперсиями s21 = s22 = 25г2 . Можно ли считать отличие выборочных
средних случайной ошибкой при уровне значимости a = 0, 01, если конкурирующая гипотеза : а) H1 : a1 ≠ a2 ; b)H1 : a1 < a2 ?
34
Б. ДИСПЕРСИИ ГЕНЕРАЛЬНЫХ СОВОКУПНОСТЕЙ НЕИЗВЕСТНЫ, НО РАВНЫ. (Малые независимые выборки, n, m < 30).
Пусть Х и У - нормально распределенные генеральные совокупности объемов n и m соответственно, S20X и S20Y - исправленные выборочные дисперсии Х и У. Предполагается, что D(X ) = D(Y ), хотя дисперсии и неизвестны. Рассматривается нулевая гипотеза H0 : M(X ) = M(Y ) при уровне
значимости a.
1) Конкурирующая гипотеза H1 : M(X ) ≠ M(Y ).
По выборкам (X1 , . . . , Xn ) и (Y1 , . . . ,Ym )вычисляется наблюдаемое
значение критерия
Tнабл = s
X −Y
.
nsX + mS20Y 1
1
+
n+m−2 n m
2
(4)
По таблице критических точек для распределения Стьюдента по заданному
уровню значимости a, помещенному в верхней строке таблицы, и числу стекр
пеней свободы k = n + m − 2 находится критическая точка tдвукр (a, k). Если
кр
|Tнабл |< tдвукр , то нет оснований отвергнуть гипотезу H0 . Если |Tнабл |>
кр
, то нулевая гипотеза отвергается.
tдвукр
2) Конкурирующая гипотеза H1 : M(X ) > M(Y ). По таблице критичекр
ских точек распределения Стьюдента находится критическая точка tпр (a, k).
по уровню значимости a, поиещенному в нижней строке таблицы, и по чискр
лу степеней свободы k = n + m − 2. Если Tнабл < tпр , то нет оснований
кр
отвергнуть нулевую гипотезу. Если Tнабл > tпр , то нулевая гипотеза отвергается.
3) Конкурирующая гипотеза H1 : M(X ) < M(Y ). Сначала находят
кр
кр
кр
критическую точку tпр , как и в п.2), и полагают tлев = −tпр . Если Tнабл >
кр
кр
tлев , то нет оснований отвергать гипотезу H0 . Если Tнабл < tлев
, то нулевая
гипотеза отвергается.
2.26 Из нормально распределенных генеральных совокупностей X и Y ,
имеющих неизвестные, но равные дисперсии, извлечены выборки
совокупность X
совокупность Y
Xi 25 35 45 Y j 20 30 40 50
ni
3
3
4
mj 3
3
4
5
При уровне значимости a = 0, 02 проверить гипотезу H0 : M(X ) = M(Y )
при конкурирующей гипотезе H1 : M(X ) ≠ M(Y ).
РЕШЕНИЕ. Вычисляем выборочные средние и выборочные исправленные
дисперсии
35
X=
S20X =
3
4
1 X
1 X
Xi ni = 36; Y =
Y m = 37, 33;
10 i=1
m j =1 j j
4
1 X
(Xi −X )2 ni = 3, 916; S20Y =
(Y j −Y )2 m j = 6, 1.
3 − 1 i =1
4 − 1 j =1
1
3
X
Вычисляем
Tнабл = s
36 − 37, 33
1, 33
= − 5, 162 = −o, 258.
1
10 · 15, 33 + 15 · 37, 27 1
+
23
10 15
По таблице критических точек распределения Стьюдента, по заданному уровню значимости a = 0, 02, помещенному в верхней строке таблице, и числу
кр
степеней свободы k = m + n − 2 = 23, находим tдвукр (0, 02, 23) = 2, 50. Так
кр
как |Tнабл | = 0, 258 < tдвукр = 2, 5, то нет оснований отвергнуть нулевую
гипотезу.
2.27 По двум независимым выборкам, объемы которых n = 10, m = 8,
извлеченным из нормальных генеральных совокупностей с неизвестными
но равными дисперсиями, найдены выборочные средние X = 142, 3, Y =
145, 3 и исправленные выборочные дисперсии S20X = 2, 7, S20Y 3, 2. При
уровне значимости a = 0, 01 проверить нулевую гипотезу H0 : M(X ) =
M(Y ) при конкурирующей гипотезе H1 : M(X ) < M(Y ).
РЕШЕНИЕ. Вычисляем наблюдаемое значение критерия
142, 3 − 145, 3
Tнабл = s
= −3, 6.
10 · 2, 7 + 8 · 3, 2 1
1
+
16
10 8
По таблице критических точек распределения Стьюдента (односторонняя
кр
критическая область) при a = 0, 01, k = 16, находим tпр (0, 01; 16) = 2, 58.
кр
кр
Следовательно, −tпр = −2, 58, и так как Tнабл = −3, 6 < tпр = −2, 58, то
нулевая гипотеза отвергается.
2.28 По двум независимым выборкам, объемы которых n = 12 и m = 18,
извлеченным из нормальных генеральных совокупностей Х и У, найдены
выборочные средние X = 31, 2, Y = 29, 2 и исправленные дисперсии
S20X = 0, 84, S20Y = 0, 40. Требуется при уровне значимости a = 0, 05
проверить нулевую гипотезу H0 : M(X ) = M(Y ) при конкурирующей гипотезе H1 : M(X ) ≠ M(Y ).
2.29 Расходы сырья Xi и Y j на единицу продукции по старой и новой
технологиям приведены в таблице (Xi расход сырья по старой технологии,
Y j - по новой технологии, ni - число изделий по старой технологии, Y j - по
36
новой.
по старой технологии
по новой технологии
Xi 404 307 308 Y j 303 304 306 308
ni
1
4
4
mj 2
6
4
1
Предполагая, что генеральные совокупности имеют нормальное распределение с неизвестными но одинаковыми дисперсиями. Требуется при уровне значимости a = 0, 1 проверить нулевую гипотезу H0 : M(X ) = M(Y )
при конкурирующей гипотезе H1 : M(X ) ≠ M(Y ).
2.6
Проверка гипотезы о виде распределения генеральной совокупности по критерию
Пирсона (критерий x2 ).
2.6.1 Проверка гипотезы о нормальном распределении генеральной совокупности по критерию
Пусть эмпирическое распределение задано в виде последовательности
интервалов (xi ; xi+1 ) и соответствующих им частот ni (ni − сумма частот,
которые попали в интервал (xi ; xi+1 )),
(x1 ; x2 ) (x2 ; x3 ) . . . (xm ; xm+1 )
n1
n2
...
nm
Для того, чтобы при уровне значимости a проверить гипотезу о нормальном распределении генеральной совокупности, надо:
1) Вычислить (например, методом произведений) выборочную среднюю
x и выборочное среднее квадратическое отклонение S0 , причем, в качестве
вариант принимать среднее арифметическое концов интервала:
x∗i =
x i + x i +1
2
.
2) Перейти к случайной величине Z =
X − x∗
и вычислить концы инS∗0
xi − x∗
x − x∗
, zi+1 = i+1 ∗ , где S∗0 — среднее квадратическое
∗
S0
S0
отклонение, вычисленное по вариантам x∗ . Наименьшее значение Z, т.е. z1 ,
полагают равным −∞, а наибольшее zm+1 = +∞.
3) Вычислить теоретические частоты n′i = nPi , где n - объем выборки,
Pi = F(zi+1 )− F(zi ) - вероятности попадания Х в интервал (xi ; xi+1 ), F(z)
тервалов zi =
— функция Лапласа.
4) Сравнить эмпирические и теоретические частоты с помощью крите37
рия Пирсона. Для этого составляют рассчетную таблицу (см. таблицу 1), по
которой находят наблюдаемое значение критерия Пирсона
x2набл =
2
m n − n′
X
i
i
i =1
n′i
.
5) По таблице критических точек распределения x2 , по заданному уровню значимости a и числу степеней свободы k = m − 3 (m− число интервалов выборки) находится критическая точка правосторонней критической
области x2кр (a, k).
Если x2набл < x2кр , то нет оснований отвергнуть гипотезу H0 о нормальном распределении генеральной совокупности. Если x2набл > x2кр , то нулевую
гипотезу отвергают.
ЗАМЕЧАНИЕ. Интервалы, содержащие малые эмпирические частоты
(ni < 5), следует объединить, а частоты этих интервалов сложить. Если
производилось объединение интервалов, то при определении числа степеней свободы по формуле k = m − 3, следует в качестве m принять число
интервалов, оставшихся после объединения интервалов.
2.30 Пусть Х — это удой коров на молочной ферме за лактационный период (в ц), n = 30.
xi 4–6 6–8 8–10 10–12 12–14
ni
4
3
6
7
10
При уровне значимости a = 0, 05 проверить гипотезу о нормальном
распределении генеральной совокупности Х, используя критерий Пирсона.
РЕШЕНИЕ. Находим середины интервалов x∗
i =
x i + x i +1
. В качестве
2
частоты ni варианты xi принимаем число вариант, попавших в i -й интервал. Получаем дискретный вариационный ряд
x∗i
5 7 9 11 13
ni 4 3 6 7 10
Вычисляем выборочное среднее x∗ и среднее квадратическое отклонеx∗ − 9
и составим
ние s∗ . Для этого перейдем к условным вариантам ui = i
2
рассчетную таблицу
∗
ni
ui
ni ui
u2i ni
4
3
6
7
10
–2
–1
0
1
2
–8
–3
0
7
20
16
3
0
7
40
38
Произведя вычисления, получим
2
u = − = −0, 067; u2 = 2, 2; x = C + hu = 9 − 0, 134 = 8, 866;
30
r s∗ = h2 u2 − u2 = 2, 96.
Нормируем случайную величину X, т.е., перейдем к величине
X − x∗i
X − 8, 866
Z=
=
и вычисляем концы интервалов (zi , zi+1 ) :
s∗
2, 96
z i +1 =
xi+1 − x∗i
,
s∗
0,148
0,555
0,237
0,125
2,243
4,848
6,744
7,863
6,222
3,084
4
3
6
7
10
n′i
(ni − n′i )2
2p−∞
n′i
e 2 dx
2
∞
Zz − x
1
F(z) = √
39
ni
0,1480
0,3554
0,4582
0,1480
0,3554
0,383
1,059
0,383
1,059
−
−0,968
−0,293
4
3
6
7
10
Для вычисления значения критерия составим таблицу
4,848
6,744
7,863
6,222
3,084
−0,3384
−0,1141
−0,5
−0,3389
−0,1141
−0,968
−0,293
zi
ni
z i +1
F(zi )
F(zi+1 )
0,1616
0,2248
0,2621
0,2074
0,1028
pi = F(zi+1 )−
−F(zi )
n′i = npi
причем, наименьшее значение z1 полагаем равным нулю, а наибольшее, т.е.,
z6 равным ∞ . Составляем расчетную таблицу
Вычисляем с помощью таблицы значение критерия x2набл = 3, 308 и по
таблице критических точек распределения x2 находим критическую точку
x2кр (0, 05; 2) = 6, 0. Так как x2набл < x2кр , то нет оснований отвергнуть нулевую гипотезу.
2.31 Пусть Х - это месячный доход жителей региона (в руб), насчитывающего n = 1000 жителей. Из генеральной совокупности сделана выборка
(xi - месячный доход одного жителя, ni - число жителей с доходом xi ).
xi < 500 500−1000 1000−1500 1500−2000 2000−2500 á 2500
ni
58
96
239
328
147
132
При уровне значимости a = 0, 05 проверить гипотезу о нормальном
распределении генеральной совокупности Х, используя критерий Пирсона.
2.32 Величины контролируемого размера n = 80 деталей, изготовленных на одном станке (мкм), приведены в таблице
интервал xi 3,9−4,9 4,9−5,9 5,9−6,9 6,9−7,9
частота ni
25
23
19
13
При уровне значимости a = 0, 01 проверить гипотезу H0 о том, что данные получены из нормально распределенной генеральной совокупности.
2.6.2 Проверка гипотезы о равномерном распределении генеральной совокупности.
Пусть эмпирическое распределение непрерывной случайной величины
Х задано в виде последовательных интервалов (xi−1 , xi ) и соответствующих
им частот ni , причем, n =
m
P
ni - объем выборки. Необходимо. исполь-
i =1
зуя критерий Пирсона, проверить гипотезу о том. что генеральная совокупность Х имеет равномерное распределение.
Плотность равномерного распределения имеет вид
1
, если − a à x < b
f (x) = b − a
0, если x ∉ (a; b).
Проверка гипотезы проводится в несколько шагов.
1) Находятся оценки a и b для параметров a и b - концов интервала соответственно,
p
p
a = x − 3s, b = x + 3s,
где x - выборочное среднее, s - выборочное среднее квадратическое отклонение.
2) Находится оценка для плотности распределения
1
f (x) =
b−a
40
.
3) Находятся теоретические частоты
4) Сравниваются эмпирические и теоретические частоты с помощью
критерия Пирсона, приняв число степеней свободы k = m − 3, где m — число интервалов, на которые разбита выборка, — точно так же, как это было
проделано в §6,пп. 4 и 5. Заключение о принятии или не принятии гипотезы
делается точно так же, как и в §6,п.5.
2.33 Проведено n = 100испытаний, в результате каждого из которых событие А появляется в различные моменты времени. В итоге было получено
эмпирическое распределение
интервал (xi−1 − xi ) 2−4 4−6 6−8 8−10 10−12
частота ni
8
28
35
22
7
Проверить при уровне значимости a = 0, 05гипотезу H0 о том, что время появления события Х распределено равномерно.
РЕШЕНИЕ. Находим вначале оценки
√ параметров
√aи bравномерного распределения по формулам a = x − 3s, b = x + 3s,где xи s вычислены
для вариационного ряда
x∗i
3 5
7
9 11
ni 8 28 35 22 7
где x∗
i =
x i + x i +1
, i = 1, 2, 3, 4, 5, x1 = 2, x6 = 12;
2
24 + 140 + 245 + 198 + 77
x=
= 6, 84.
100
x∗ − 7
Перейдя к условным вариантам ui = i
,вычисляем выборочное квад2
s
n−1
S0X = 2, 0915.
ратическое отклонение s =
√
n√
Тогда a = x −√ 3s = 6, 84 − 32, 0915 = 3, 217, b = x +
6, 84 + 2, 0915 3 = 10, 463.
Находим плотность вероятности предполагаемого распределения
1
, если a à x < b
f (x) = 7, 246
0, если x ∉ (a; b).
√
3s =
4 − 3, 217
100 = 10, 806, n′2 =
7, 246
6−4
8−6
10 − 8
100 = 27, 601 = n′3 =
100 = n′4 =
100,
7, 246
7, 246
7, 246
10, 463 − 10
= 6, 3897.
n′5 =
7, 246
Составляем расчетную таблицу
и вычисляем теоретические частоты n′1 =
41
ni
n′i
(ni − n′i )2
n′i
8
28
35
22
7
В
10,806
0,0,7286
27,6014
0,0057
27,6014
1,9832
27,6014
1,1367
6,3897
0,0583
результате вычислений, учитывая, что число степеней свободы k =
S0 − 3 = 5 − 3 = 2,и уровень значимости a = 0, 05, находим наблюдаемое значение критерия: x2набл = 3, 9125. Поскольку x2набл = 3, 9125 <
x2 (0, 05; 2) = 6, 0,. то нет оснований отвергнуть гипотезу H0 .
2.34 Дана выборка из генеральной совокупности Х
a)
интервал (xi−1 , xi ) (−40, −30) (−30, −20) (−20, −10) (−10, 0)
частота ni
8
12
19
11
b)
интервал (xi−1 , xi ) (−1, −0, 5) (−0, 5, 0) (0, 0, 5) (0, 5, 1)
частота ni
12
20
38
30
При уровне значимости a) a = 0, 05; b) a = 0, 01проверить гипотезу
H0 о том, что случайная величина распределена равномерно.
2.6.3 Проверка гипотезы о распределении генеральной совокупности по закону Пуассона.
Пусть задано эмпирическое распределение дискретной случайной величины Х. Требуется, используя критерий Пирсона, проверить гипотезу о распределении генеральной совокупности по закону Пуассона.
Для того, чтобы при уровне значимости aпроверить, что генеральная совокупность Х распределена по закону Пуассона, надо:
1. Найти по заданному эмпирическому распределению выборочное среднее
x.
2. Приняв в качестве оценки параметра lраспределения Пуассона выборочную среднюю l = x, найти по формуле
Pi =
li −l
e , i = 0, 1, 2, . . . , r,
i!
теоретические вероятности и теоретические частоты n′i = nPi . Здесь r максимальное число различных вариант, n- объем выборки.
3. Сравнить эмпирические и теоретические частоты с помощью критерия
Пирсона (5), приняв число степеней свободы k = r − 2,где r - число различных групп выборки. Если x2набл < x2кр - нет оснований отвергнуть гипо42
тезу о распределении генеральной совокупности по закону Пуассона. Если
x2набл < x2кр - гипотеза отвергается.
Если производилось объединение малочисленных частот в одну группу,
то r - число оставшихся групп выборки после объединения.
2.35 При испытании радиоэлектронной аппаратуры фиксировалось число отказов в результате 59 испытаний
число отказов xi
0
1 2 3
число испытаний ni 42 10 4 3
Проверить гипотезу H0 о том, что при уровне значимости a = 0, 05 число
отказов имеет распределение Пуассона.
0 + 10 + 8 + 9
≅
РЕШЕНИЕ. Найдем сначала выборочную среднюю: x =
59
0, 5. Полагаем l = x = 0, 5. Найдем по готовым таблицам или по формуле
li −l
e вероятности. Получаем, p0 = e−0,5 = 0, 606, p1 = 0, 5e−0,5 =
i!
0, 53 −0,5
0, 52 −0,5
e
= 0, 076, p3 =
e
= 0, 013. Находим
0, 303, p2 =
2
6
′
′
теоретические частоты ni = npi : n0 = 35, 785, n1 = 17, 893, n′2 =
4, 473, n′3 = 0, 522.Составляем расчетную таблицу, объединяя последние
два значения ni в одно
(ni − n′i )2
ni
n′i
n′i
Pi =
42 35,785
1,079
10 17,893
3,482
7
5,219
0,608
Вычисления дают следующее значение наблюдаемого критерия x2набл =
5, 169. Находим критическую точку распределения x2 при уровне значимости a = 0, 05и с k = 3 − 1 = 2степенями свободы: x2кр (0, 05; 2) = 6, 0.Так
как x2набл = 5, 169 < x2кр = 6, 0, то нет оснований отвергнуть нулевую гипотезу.
2.36 В цехе с четырмя станками ежедневно регистрировалось число вышедших из строя станков. Всего было проведено 50 наблюдений, результаты
приведены в таблице
число слом. станковxi
0 1
2 3 4
число зарегистр. случаевni 6 14 17 7 6
При уровне значимости a = 0, 05проверить гипотезу H0 о том, что число вышедших из строя станков имеет распределение Пуассона.
2.37 В итоге проверки на стандартность 200 ящиков консервов получено
следующее эмпирическое распределение значений случайной величины Х
— числа нестандартных банок консервов в одном ящике:
43
0
1
2 3 4
132 43 20 3 2
Проверить при уровне значимости a = 0, 05гипотезу H0 о том, что число нестандартных коробок распределено по закону Пуассона.
xi
ni
ОТВЕТЫ И УКАЗАНИЯ.
2.3 H0 : a0 = 10л, H1 = a < 10л, Uнабл = −3, uкр = 1, 64. Гипотеза H0
отвергается.
48 − 49
2.4 Uнабл =
· 3 = −1, uкр = 1, 96. Нет оснований отвергнуть
3
нулевую гипотезу.
x−2
2.5 Uнабл =
· 4 = x − 2 = 1, uкр = 1, 65. Нет оснований отвергнуть
4
нулевую гипотезу.
865 − 800 √
кр
кр
· 17 = 2, 233, tпр (0, 01; 16) = 2, 92, Tнабл < tпр .
2.8 Tнабл =
120
Нет оснований отвергнуть нулевую гипотезу.
кр
кр
2.9 H0 : a = 75, H1 : a ≠ 75, tдвуст = 1, 83, |Tнабл | < tдвуст . Нет оснований
отвергнуть нулевую гипотезу.
s
n
1 P
175
2.10 a)x =
(x − x)2 = 0, 163; b)Tнабл =
= 35, 045, S0 =
20
n − 1 i =1 i
35, 042 − 35 √
кр
20 = 0, 9; tдвуст (0, 05; 19) = 2, 09. Нет оснований отверг0, 163
нуть нулевую гипотезу.
0, 325 √
кр
· 70 = 13, 711, tпр (0, 01; 79) = 2, 39, x = 8, 325, S0 =
2.11 Tнабл =
0, 212
кр
кр
0, 212. Так как Tнабл > −tпр = tлев , то нет оснований отвергать гипотезу
H0 .
кр
2.12 x = 5, 989, S0 = 12, 124, Tнабл = 0, 009, tпр (0, 05; 89) = 1, 67 >
Tнабл . Нет оснований отвергнуть нулевую гипотезу.
2.15 Гипотеза H0 отвергается.
(n − 1)S20
(21 − 1)16, 2
=
= 21, 6 < x2кр (0, 01, 20) = 37, 6.
2.16 x2набл =
15
s20
Нет оснований отвергнуть нулевую гипотезу.
2.17 S20u = S20x = 4, x2лев кр (0, 975, 19) = 8, 91. x2прав кр (0, 0б025, 19) =
32, 9б, x2набл = 38. Гипотеза H0 отвергается.
2.21 Fнабл = 1, 5, Fкр (0, 05; 20, 15) = 2, 33 (k1 = 21, k2 = 16) . Гипотеза
левосторонняя. Так как Fкр = 2, 33 > Fнабл = 1, 5, то нет оснований отвергнуть нулевую гипотезу.
2.22 x = 6, 333, y = 6, 47, S20X = 0, 604, S20Y = 0, 524, k1 = 11, k2 =
16. Fнабл = 1, 153, Fкр (0, 05; 11, 16) = 2, 72, Fкр > Fнабл . Нет оснований
44
отвергнуть нулевую гипотезу.
2.23 a)S20X = 5, 9697, S20Y = 5, 174, Fнабл = 1, 1538, Fкр (0, 01; 11, 11) =
4, 46. Нет оснований отвергнуть нулевую гипотезу.
b)S20X = 1, 61, S20Y = 2, 1923, Fнабл = 1, 3617, Fкр (0, 01; 12, 8) = 5, 67.
Нет оснований отвергнуть нулевую гипотезу.
2.25 a)Гипотеза H0 не отвергается. b)Гипотеза H0 не отвергается.
кр
2.28 Tнабл = 7, 1, k = 28, a = 0, 05; tдвуст (0, 05; 28) = 2, 05. Гипотеза H0
отвергается.
кр
2.29 Tнабл = 4, 722, tдвуст (0, 1; 20) = 1, 725. Гипотеза H0 отвергается.
2
2.31 x = 1653, s = 445591. x2набл = 2, 37 < x2кр (0, 05, 2) = 5, 99. Нет
оснований отвергнуть нулевую гипотезу.
x∗i − 5, 65
x i + x i +1 ∗
,
x
=
5
,
65
,
u
=
, u = −0, 75, u2 =
32. x∗
=
i
i
i
2
1
∗
xi − x
, i = 2, 3, 4, z5 =
s∗
= 3, 218, S0 = 4 − 3 =
p
1, 7, s∗ = 1, 7 − 0, 752 = 1, 0665, z1 = −∞, zi =
∞, pi = F(zi+1 ) − F(zi ), ni = 80 pi . x2набл
1, x2кр (0, 01, 1) = 6, 6 > x2набл . Нет оснований отвергнуть нулевую гипоте-
зу.
x∗i
-35 -25 -15 -5
ni
8
12
19 11
√
∗
∗
xi = −18, 4, sv = 9, 922, a = −18, 4 − 9, 922 3 = −35, 585, b =
2.34 а)
√
−18, 4+9, 922 3 = −, 1, 215, f (x) =
1
, x2 = 1, 7399, k =
34, 37 набл
4 − 3 = 1, x2кр (0, 05, 1) = 3, 8. Нет оснований отвергнуть нулевую гипотезу.
x∗ -0,75 -0,25 0,25 0,75
b) i
ni
8
12
20
38
1
1
x∗i = −0, 18, s∗v = 0, 49, a = −0, 6687, b = 1, 0287,
,
=
b − a 1, 6974
x2набл = 5, 9834, x2кр (0, 025, 1) = 5. Гипотеза H0 отвергается.
2.36 x = 1, 86, l = 2 (округляем до ближайшего целого числа). Pi =
1
b−a
=
li −l
e , i = 0, 1, 2, 3, 4, 5. x2набл = 1, 93619, x2кр (0, 05, 3) = 7, 8. Нет осноi!
ваний отвергнуть нулевую гипотезу.
(43 + 40 + 9 + 8)
2.37 x =
= 0, 5 = l. Pi = (0, 5)i i !e−0,5 , i = 0, 1, 2, 3, 4, 5.
200
При вычислении x2набл малочисленные частоты последних двух групп объединяются. x2набл = 9, 4072, x2кр (0, 05, 2) = 6, 0(k = 4 − 2 = 2). Гипотеза
H0 отвергается.
45
Глава 3
Метод наименьших квадратов
и элементы регрессионного
анализа.
3.1
Предварительные сведения. Метод
наименьших квадратов.
Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из
них и условным математическим ожиданием другой. Между переменными
корреляционная зависимость может быть представлена в виде
M(Y |X = x) = w(x), M(X |Y = y) = c(y).
Эти уравнения называются уравнениями регрессии соответственно Y на X
и X на Y . Графики функций y = w(x)и x = c(y)называются линиями
регрессии. По выборке
X
Y
x1
y1
x2
y2
...
...
xn
yn
ищут оценку функций регрессии. Одной из основных задач регрессионного
анализа является изучение формы зависимости между переменными X и
Y.
Вначале делается предположение о виде функции регрессии
y = w(x, a1 , . . . , am ), где a1 , a2 , . . . , am — параметры предполагаемой функции. Затем определяют параметры ai методом наименьших квадратов, т.е.,
46
ищут такие значения параметров a1 , a2 , . . . , am , при которых достигается
минимум функции
S=
n
X
i =1
(yi − w(xi , a1 , . . . , am ))2 .
Мы далее рассмотрим только случай линейной зависимости с двумя параметрами, а именно,
y = w(x, a1 , a2 ) = a2 + a1 x.
Тогда
S=
n
X
(yi − a1 xi − a2 )2 .
(6)
i =1
Исследуем функцию S на экстремум, как функцию двух переменных a1 и a2 .
Вначале находим критические точки из системы уравнений
n
X
∂w
(x, a1 , a2 ) = −2 (yi − a1 xi − a2 )xi = 0,
∂a1
i =1
n
X
∂w
(x, a1 , a2 ) = −2 (yi − a1 xi − a2 ) = 0.
∂a2
i =1
Решениями этой системы будут величины
a1 =
где x =
x·y−x·y
,
x2 − (x)2
n
1 P
xi , y =
n
1 P
a2 =
yi , xy =
n
1 P
y · x2 − x · xy
= y − a1 x,
x2 − (x)2
xi yi , x2 =
n i =1
n i =1
n i =1
регрессии Y на X принимает следующий вид
y = a2 + a1 x.
n
1 P
(xi )2 . Уравнение
n i =1
(7)
Учитывая, что выборочный коэффициент корреляции имеет вид
rв =
q
xy − xy
,
sX sY
q
(8)
где sX = x2 − (x)2 , sY = y2 − (y)2 , из равенства (7) следует
y = a2 +
sY
rx.
sX
Полученные с помощью метода наименьших квадратов оценки параметров уравнения регрессии a1 и a2 , являются несмещенными и состоятельными. Можно показать, что рассматриваемые оценки являются эффективными в классе линейных несмещенных оценок.
47
3.1 Для определения параметров a1 и a2 в уравнении регрессии y = a1 x+
a2 были измерены значения y при различных значениях x. получена выборка (x1 , y1 ), ..., (xn , yn ). Методом наименьших квадратов определить параметры a1 и a2 .
xi 40 50 60 70 80 90 100
yi 20 25 28 30 35 40 45
РЕШЕНИЕ. Делаем предварительные вычисления
1
223
x = · 490 = 70, y =
= 31, 8571,
7
7
1
xy = (800 + 1250 + 1680 + 2100 + 2800 + 3600 + 4500) = 2390,
7
1
x2 = 402 + 502 + 602 + 702 + 802 + 902 + 1002 = 5300.
7
Вычисляем коэффициенты уравнения регрессии
2390 − 70 · 31, 857
a1 = 5300 − 4900 = 0, 400025, a2 = 31, 857 − 0, 400025 · 70 = 3, 85525.
Уравнение регрессии Y на X имеет вид y = 0, 400025x + 3, 85525.
3.2 Для определения параметров a1 и a2 в уравнении регрессии y =
a1 x + a2 были измерены значения y при различных значениях x. Получена
выборка (x1 , y1 ), ..., (xn , yn ). Методом наименьших квадратов определить
параметры a1 и a2 .
a)
xi 2 3
4
5
6
7
8
yi 2 1,9 2,2 2,4 2,3 2,5 2,5
b)
xi
yi
11,0
1,5
11,5
1,5
12,0
1,6
12,5
1,7
13,0
1,9
13,5
1,9
c)
xi
yi
-0,75
1,83
-0,5
1,57
-0,25
1,13
0
0,89
0,25
0,75
0,5
0,30
0,75
0,06
1
-0,01
-1
2,08
d)
xi
yi
3.2
0,5
3
1
3
1,5
4
2
4
2,5
4
3
5
3,5
5
4
5
4,5
6
5
8
Проверка гипотезы о значимости выборочного
коэффициента корреляции.
Пусть двумерная генеральная совокупность (X,Y ) распределена нормально. Из этой совокупности извлечена выборка объема n и по ней най48
ден выборочный коэффициент корреляции r. Требуется проверить нулевую
гипотезу H0 : rG = 0, где rG - коэффициент корреляции генеральной совокупности (X,Y ).
Для того, чтобы при уровне значимости a проверить нулевую гипотезу
при конкурирующей гипотезе H1 : rG ≠ 0, надо вычислить наблюдаемое
значение критерия
√
r n−2
Tнабл = p
,
1 − r2
где r определяется формулой (8), и по таблице критических точек распределения Стьюдента, по заданному уровню значимости a и числу степеней
свободы k = n − 2 найти критическую точку tкр двусторонней критической
области. Если |Tнабл | < tкр , то нет оснований отвергнуть гипотезу H0 . Если
|Tнабл | > tкр ,то нелевая гипотеза отвергается.
3.3 По выборке объема n = 100, извлеченной из двумерной нормальной
генеральной совокупности (X,Y ), найден выборочный коэффициент корреляции r = 0, 2. . Требуется при уровне значимости a = 0, 05 проверить
нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе H1 : rG ≠ 0.
РЕШЕНИЕ. Находим наблюдаемое (эмпирическое) значение критерия
Tнабл
√
100 − 2
= 0, 2 p
= 2, 02.
1 − 0, 22
По таблице критических точек распределения Стьюдента по уровню значимости a = 0, 05, помещенному в верхней строке таблицы, и числу степеней
свободы k = n − 2 = 98 находим критическую точку двусторонней критической области кр(0, 05; 98) = 1, 96. Поскольку Tнабл = 2, 02 > 1, 96 = tкр ,
то нулевую гипотезу отвергаем, т.е., случайные величины Х и У коррелированы.
3.4 По выборке объема n = 50 , извлеченной из двумерной нормальной
генеральной совокупности (X,Y ), составлена корреляционная таблица
X
12
Y
105
115
125
135
145
17
22
4
3
−
27
37
mj
7
16
−
1
−
4
13
− −
−
8
2
1
11
1
2
−
−
−
−
3
ni
6
9
6
12 12
5
50
Требуется: а) Найти выборочный коэффициент корреляции r . b) При
уровне значимости a = 0, 05 проверить нулевую гипотезу H0 : rxy = 0 при
−
2
3
1
5
3
32
−
−
10
−
−
49
конкурирующей гипотезе H1 : rxy ≠ 0.
РЕШЕНИЕ. Перейдем к новым вариантам
y j − 125
x − 27
, vj =
.
ui = i
5
10
Составим корреляционную таблицу для величин U и V
U
−3
V
−2
−1
−2
−1
4
3
−
0
1
mj
7
16
0
−
1
− 4
13
1
−
−
−
8
2
1
11
2
1
2
−
− − −
3
ni
6
9
6
12 12 5 50
Поскольку выборочный коэффициент корреляции rxy , то ввиду того, что
m
n P
1 P
−
2
3
3
2
1
5
−
−
−
−
10
u v n − uv
n i =1 j =1 i j i j
rxy = ruv =
,
su sv
где
u=
v=
n
1 X1
n i =1
n
1 X2
n
j =1
ui ni , u2 =
v j m j , v2 =
n1
X
i =1
q
u2i ni , su = u2 − (u)2 ,
n
1 X2
n
j =1
q
m j , sv = v2 − (v)2 ,
нам надо вычислить эти величины и величину
n2
n1 P
1 P
n i =1 j =1
ui v j ni j , n = 50.
Для вычисления u, v, u2 , v2 , составим расчетные таблицы
совокупность V
совокупность U
ui
ni
ni ui
ni u2i
vj
−3
−2
−1
6
9
6
12
5
−18
−18
−6
54
36
6
0
20
−2
−1
mj
mjvj
m j v2j
7
−14
28
16
−16
16
0 13
0
0
0
0
1
11
11
11
2
10
2
3
6
12
20
13
= −0, 4; v = −
= −0, 26; u2 =
Отсюда следует, что u = −
50
50
p
67
128
= 2, 56; v2 =
= 1, 34; su = 2, 56 − 0, 16 = 1, 55; sv =
50
50
p
1, 34 − 0, 0676 = 1, 13.
50
Контроль
=9
P
-7
0
-8
2
0
0
8
2
8
0
0
1
i =1 j =1
4
-7
2
0
u
u·V
P
2
1
V =
P
nuv·v
2
0
0
0
1
3
-9
-3
-3
-2
n2
n1 P
P
14
-4
0
1
-1
-5
-1
5
1
-6
3
-6
2
-1
v
-2
-8
2
2
-10
-1
-6
-8
-3
u
Таким образом,
2
1 1
4
10
10
0
3
-8
4
-1
8
2
P
4
-6
-3
-8
↑
=9
-14
4
0
3
16
v
P
U
P=
nuv· u
2
1
0
-1
-2
↑
v ·U
Для вычисления используем таблицу
ui v j ni j = 9 и
1
· 9 − (−0, 4)(−0, 26)
50
= 0, 0434.
ruv =
1, 55 · 1, 13
Проверим нулевую гипотезу H0 : rxy = 0 при уровне значимости a = 0, 05,
51
при k = n − 2 = 48 степенях свободы и при конкурирующей гипотезе H1 :
rxy ≠ 0. Находим по таблице критических точек распределения
Стьюдента
√
48
= 0, 307 <
1 − 0, 04342
tкр = 2, 02, то нет оснований отвергнуть нулевую гипотезу.
3.5 По выборке объема n = 25, извлеченной из двумерной нормальной
генеральной совокупности (X,Y ). Требуется: а) Составить корреляционную таблицу. б) Найти выборочный коэффициент корреляции rxy . в) Проверить нулевую гипотезу Ho : rG = 0 при уровне значимости a = 0, 01 и
при конкурирующей гипотезе H1 : rG ≠ 0.
X 20 35 40 30 25 35 20 30 25 35 40 30 20
Y 10 30 20 40 10 20 40 40 10 40 20 10 30
X 25 35 30 20 40 20 30 30 30 20 30 40
Y 40 20 30 40 10 10 30 20 40 20 10 30
РЕШЕНИЕ. а) Составляем корреляционную таблицу
tкр (0, 05; 48) = 2, 02. Так как Tнабл = 0, 0434 · p
X
Y 20
25
30
35
40
mj
10
20
30
40
2
−
−
2
1
2
3
8
−
1
1
1
1
4
7
5
5
8
25
2
1
1
2
6
ni
1
3
2
1
1
4
б) Введем новые варианты ui =
xi − 30
,
5
корреляционную таблицу для вариант ui и v j .
U
−2
V
−2
−1
0
1
ni
2
1
1
2
6
−1
0
1
2
mj
2
2
1
2
3
8
−
1
1
1
1
4
7
5
5
8
25
−
−
1
3
2
1
1
4
vj =
y j − 30
10
и составим
5 P
4
1 P
ui v j ni j .
25 i=1 j =1
3
11
63
Получаем u = −
= −0, 12, v = −
= −0, 44, u2 =
=
25
25
25
2, 52,pv2 = 1, 64,
p
su = 2, 52 − (0, 12)2 = 1, 583, sv = 1, 64 − 0, 1936 = 1, 203.
Вычислим величины u, v, su , sv ,
52
совокупность U
ui
ni
ni ui
−2
−1
6
3
8
4
4
−12
−3
совокупность V
ni u2i
vj
mj
mjvj
m j v2j
=4
P
P
-2
1
-4
2
1
1
-1
-1
1
1
-2
0
-3
3
-3
6
0
3
2
-1
-4
u
2
2
0
0
1
53
V =
P
nuv·v
P
u·V
-2
1
-1
-1
v
-2
u
-4
2
1
-2
-4
-4
1
2
1
-1
-2
-4
3
0
0
0
-2
0
1
0
2
-2
1
0
2
1
2
1
-2
-1
1
1
2
2
2
-4
2
1
2
1
0
-1
-2
↑
←
Контроль
=4
-2
0
-2
8
v
U=
P
nuv· u
P
v ·U
24
−2
7
−14
28
3
−1
5
−5
5
0
0
0
0
5
0
0
1
4
4
1
8
8
8
2
8
32
3
4 P
1 P
Для вычисления
ui v j ni j составляем таблицу
25 i=1 j =1
Вычисления дают следующий результат:
5 P
4
1 P
n i =1 j =1
ui v j ni j =
4
= 0, 16,
25
0, 16 − (−0, 12)(−0, 44)
rxy = ruv =
= −0, 193.
1, 583 · 1, 203
Проверим нулевую гипотезу H0 : rG = 0, при уровне значимости a =
0, 05 и конкурирующей гипотезе H1 : rG ≠ 0. Имеем, k = n − 2 = 23. Находим по таблице критических точек распределения Стьюдента критическую
√
23
=
точку tкр (0, 01; 23) = 2, 81. Вычисляем Tнабл = −0, 193 p
1 − (0, 193)2
−0, 943. Так как |Tнабл | = 0, 943 < tкр = 2, 81, то нет оснований отвергать
нулевую гипотезу.
3.6 По выборке объема n = 120, извлеченной из нормальной двумерной
генеральной совокупности (X,Y ), найден выборочный коэффициент корреляции rxy = 0, 4. Требуется при уровне значимости a = 0, 05 проверить
нулевую гипотезу о равенстве нулю генерального коэффициента корреляции при конкурирующей гипотезе H1 : rG ≠ 0.
3.7 По выборке объема n = 30, извлеченной из нормальной двумерной
генеральной совокупности (X,Y ), составлена корреляционная таблица
X
Y 10
15
20
25
14 − −
4
2
24 2
1
−
3
34 −
4
2
1
44
1
2
8
−
Требуется а) Найти выборочный коэффициент корреляции rxy . б) При
уровне значимости a = 0, 01 проверить нулевую гипотезу Ho : rG = 0 при
конкурирующей гипотезе H1 : rG ≠ 0.
3.8 По выборке объема n = 24, извлеченной из двумерной нормальной генеральной совокупности (X,Y ), требуется: а) Составить корреляционную таблицу. б) Найти выборочный коэффициент корреляции rxy . в)
При уровне значимости a = 0, 01 проверить нулевую гипотезу Ho : rG = 0
при конкурирующей гипотезе H1 : rG ≠ 0.
X 5 15 5 10 15 20 5 15 15 5 15 10 15
Y 14 24 34 14 24 40 14 34 24 40 14 24 14
X 20 15 15 5 10 15 15 5 15 20 15
Y 40 24 14 24 34 14 40 14 24 34 24
54
3.3
Уравнения линейной регрессии.
3.9 Для определения параметров a1 и a2 в уравнении регрессии y =
a1 x + a2 были измерены значения y при различных значениях x. Получена
выборка (x1 , y1 ), . . . , (xn , yn ) объема n = 5. Методом наименьших квадратов определить параметры уравнения регрессии a1 и a2 .
xi 40 50 60 70 80
yi 20 25 28 30 35
РЕШЕНИЕ. Вычисляем вначале величины x, y, x2 , y2 , xy. Получаем
300
1
= 60. y = (20 + 25 + 28 + 30 + 35) =
5
5
5
5
19000
3934
138
1 P
1 P
x2i =
y2 =
= 2, 76, x2 =
= 3800, y2 =
=
5
5 i =1
5
5 i =1 i
5
5
8630
1 P
7868, xy =
= 1726. Находим коэффициенты уравнеxi yi =
5 i =1
5
1726 − 60 · 2, 76
xy − xy
y · x2 − xxy
ния a1 =
=
=
= 7, 802. a2 =
3800 − 3600
x2 − (x)2
x2 − (x)2
2, 76 · 3800 − 60 · 7, 802
= 50, 099.
3800 − 3600
Записываем уравнение регрессии Y на X : y = 7, 802x + 50, 099.
3.10 В корреляционной таблице дана выборка значений двумерной генеральной совокупности (X,Y )
1
5
x = (40 + 50 + 60 + 70 + 80) =
X
Y
0, 5
2, 0
3, 5
nx
4
6
8
10
ny
4 – 2 2
8
– 6 – –
6
– 3 1 2
6
4 9 3 4 n = 20
Найти линейное уравнение регрессии Y на X .
РЕШЕНИЕ. Перейдем к новым вариантам ui =
составим расчетные таблицы
совокупность U
ui
ni
ni ui
ni u2i
xi − 8
2
, vj =
yj − 2
и
1, 5
совокупность V
vj
mj
mjvj
m j v2
j
4
−8
16
−1
8
−8
8
9
−9
9
0
6
0
0
0
3
0
0
1
6
6
6
1
4
4
4
Производя необходимые вычисления, находим u = −0, 65; u2 = 1, 45; v =
−0, 1; v2 = 0, 7. Учитывая, что C1 = 8, C2 = 2, h1 = 2, h2 = 1, 5, вычис-
−2
−1
55
q
ляем далее x = uh
+C1 = 6, 7, y = vh2 +C2 = 1, 85, sx = h1 u2 − (u)2 =
q1
2, 028, sy = h2 v2 − (v)2 = 1, 245.
Для нахождения выборочного коэффициента корреляции составляем расчетную таблицу
u
-2
-1
-8
1
2
-4
P
v ·U
v
2
0
4
-1
U=
P
nuv· u
1
0
v
-6
6
-6
0
-1
-1
-2
-2
-6
6
0
0
0
-3
3
1
3
V =
P
nuv·v
P
u·V
2
1
2
2
-4
3
-1
0
8
-3
0
0
u
P
P
=5
↑
=5
↑
1
Контроль
Подставляя найденные значения в уравнение
sy
(x − x),
sx
получаем наше уравнение регрессии Y на X
y = 0, 153x + 0, 821.
3.11 Для определения параметров a1 и a2 в уравнении регрессии y =
a1 x + a2 были измерены значения y при различных значениях x. Получена выборка (x1 , y1 ), . . . , (xn , yn ). Методом наименьших квадратов определить параметры a1 и a2 .
xi 11,0 11,5 12,0 12,5 13,0
а)
yi
1,5
1,5
1,6
1,7
1,9
xi 0,5 1 1,5 2 2,5
b)
yi
3
3
4
4
5
y − y = rxy
3.12 В корреляционной таблице дана выборка значений двумерной генеральной совокупности (X,Y ). Найти линейное уравнение регрессии Y на
X.
56
X
5
Y
10
15
X
0
Y
20
1
2
3
4
− 1
2 3
8
2 − 5 −
−
2
4
12 2 3 − −
4 −
3
−
16 − − 1
1
3.13 Для определения параметров a1 и a2 в уравнении регрессии y =
a1 x + a2 были измерены значения y при различных значениях x. Получена
выборка (x1 , y1 ), . . . , (xn , yn ). Требуется: а) Найти выборочный коэффициент корреляции rxy . б) При уровне значимости a = 0, 05 проверить нулевую гипотезу H0 : rG = 0 при конкурирующей гипотезе H1 : rG ≠ 0. в)
Найти выборочное линейное уравнение регрессии Y и X .
xi
-1
-0,75 -0,5 -0,25
а)
yi 1,09 1,47 1,95 2,47
xi 2 3
4
5
6
b)
yi 2 1,9 2,2 2,4 2,3
3.14 В корреляционной таблице дана выборка значений двумерной генеральной совокупности (X,Y ). Требуется: а) найти выборочный коэффициент корреляции rxy ; б) при уровне значимости a = 0, 01 проверить нулевую
гипотезу H0 : rG = 0 при конкурирующей гипотезе H1 : rG ≠ 0; в) найти
выборочное линейное уравнение регрессии Y и X .
a)
b)
а) 1
2
3
3
X
1
Y
2
4
6
nx
–
1
2
3
2
2
−
b)
−
2
3
4
ny
2
2
–
4
3
–
5
8
–
4
1
5
5
7
8
n = 20
X
0, 5
Y
0, 6
–
0, 7
1
0, 8
1
0, 9
–
nx
2
0, 6
0, 7
0, 8
ny
2
4
–
–
6
–
–
3
–
3
8
–
–
1
9
10
5
4
1
n = 20
ОТВЕТЫ И УКАЗАНИЯ.
3.2 a) x = 70, y = 31, 857, xy = 2390, x2 = 5300, a1 = 0, 400, a2 =
3, 855. y = 0, 400x + 3, 855.
b) x = 5, y = 2, 2571, xy = 11, 6857, x2 = 29, a1 = 0, 10005, a2 =
1, 75685. y = 0, 10005x + 1, 7568.
c) x = 12, 25, y = 1, 6333, xy = 20, 7583, x2 = 96, 4167, a1 = −0, 01399,
a2 = 1, 8047. y = −0, 01399x + 1, 8047.
d) x = 0, y = 0, 3356, xy = −0, 4608, x2 = 0, 4167, a1 = −1, 1058, a2 =
0, 3356. y = −1, 1058x + 0, 3356.
57
e) x = 2, 75, y = 4, 7, xy = 15, 8, x2 = 9, 625, a1 = 1, 39034, a2 =
0, 876565. y = 1, 39034xs+ 0, 876565.
11800
= 4, 74, tкр (0, 05; 118) = 1, 98. Гипотеза
3.6 r = 0, 4, Tнабл = 0, 4
84
H0 отвергается.
y j − 24
xi − 15
, vj =
.u =
3.7 Перейти к условным вариантам ui =
5
10
0, 8333, u2 = 2, 6333, v = 0, 7667, v2 = 1, 9, su = 1, 3924, v2 =
1, 1455,
√
28
ruv = rxy = −0, 1289. Tнабл = −0, 1289 p
= −0, 6878, k =
1 − 0, 12892
28,
tкр (0, 01; 28) = 2, 76. Нет оснований отвергнуть нулевую гипотезу.
3.8 Сначала по выборке, извлеченной из двумерной из двумерной нормальной генеральной совокупности (X,Y ) составить корреляционную таблицу.
y j − 24
xi − 10
, vj =
. Тогда u =
Перейти к условным вариантам ui =
5
10
2
2
0, 5, u = 1, 25, v = 0, 1667, v = 1, 1667, su = 1, sv = 1, 0672, ruv =
rxy = 0, 1796. Tнабл = 0, 8563, tкр (0, 01; 22) = 2, 82. Нет оснований отвергнуть нулевую гипотезу.
yj − 2
xi − 10
3.11 a) Перейти к условным вариантам ui =
, vj =
. То5
1
гда u = 0, 25, u2 = 1, 4, v = 0, 1, v2 = 0, 6, sx = 5, 7825, sy =
0, 7681, rxy = 0, 08443, x = 11, 25, y = 2, 1. y = 0, 0844x + 1, 1505.
y j − 12
xi − 2
b) Перейти к условным вариантам ui =
, vj =
. Тогда u =
1
1
2
2
−0, 4, u = 1, 2, v = 0, 85, v = 1, 65, sx = 1, 0198, sy = 3, 852, rxy =
0, 3971, x = 1, 6, y = 15, 4. y = 1, 5x − 2, 4.
3.12 a) rxy = 0, 811. Tнабл = 1, 96, tкр (0, 05; 2) = 4, 30. Нет оснований
отвергнуть нулевую гипотезу. a1 = 1, 22067, a2 = 2, 511, y = 1, 22067x +
2, 511.
b) rxy = 0, 8236. Tнабл = 2, 515, tкр (0, 05; 3) = 3, 18. Нет оснований отвергнуть нулевую гипотезу. a1 = 0, 11, a2 = 1, 72, y = 0, 11x + 1, 72.
3.14 a) rxy = −0, 0127, Tнабл = −0, 2286, tкр (0, 01; 18) = 2, 88. Нет оснований отвергнуть нулевую гипотезу. a1 = −0, 02527, a2 = 4, 3694985, y =
−0, 02527x + 4, 3694985.
b) rxy = −0, 312, Tнабл = −1, 3932, tкр (0, 01; 18) = 2, 88. Нет оснований отвергнуть нулевую гипотезу. a1 = −0, 270, a2 = 0, 8677, y =
−0, 270x + 0, 8677.
58
0
1
2
3
4
5
6
l
0,2
0,81873
0,16375
0,01638
0,00109
0,00006
0,1
0,90484
0,09048
0,00452
0,00015
i
k
0
1
2
3
4
5
6
7
8
l
2,0
0,13534
0,27067
0,27067
0,18045
0,09022
0,03609
0,01203
0,00344
0,00086
1,0
0,36788
0,36788
0,18394
0,06131
0,01533
0,00307
0,00051
0,00007
0,00001
Т а б л. 1. (Окончание).
k
0,3
lk −l
e
k!
0,04979
0,14936
0,22404
0,22404
0,16803
0,10082
0,05041
0,02160
0,00810
3,0
0,74082
0,22225
0,03334
0,00333
0,00025
0,00002
Т а б л. 1. Значения функции pk (l) =
Распределение Пуассона
0,01832
0,07326
0,14653
0,19537
0,19537
0,15629
0,10419
0,05954
0,02977
4,0
0,67032
0,26813
0,05363
0,00715
0,00072
0,00006
0,4
0,00674
0,03369
0,08422
0,14037
0,17547
0,17547
0,14622
0,10445
0,06528
5,0
0,60653
0,30327
0,07582
0,01264
0,00158
0,00016
0,00001
0,5
k
9
10
11
12
13
14
15
16
17
l
0,54881
0,32929
0,09879
0,01976
0,00296
0,00036
0,00004
0,6
0,00019
0,00004
0,00001
2,0
0,49659
0,34761
0,12161
0,02839
0,00497
0,00070
0,00008
0,00001
0,7
0,00270
0,00081
0,00022
0,00006
0,00001
3,0
0,44933
0,35946
0,14379
0,03834
0,00767
0,00123
0,00016
0,00002
0,8
0,01323
0,00529
0,00193
0,00064
0,00020
0,00006
0,00002
4,0
0,40657
0,36591
0,16466
0,04940
0,01112
0,00200
0,00030
0,00004
0,9
5,0
0,03627
0,0813
0,00824
0,00343
0,00132
0,00047
0,00016
0,00005
0,00001
Приложение. Таблицы
Т а б л. 2. Значения функции
l
k
0
1
2
3
4
5
l
k
0
1
2
3
4
5
6
7
8
9
10
11
12
13
k lm e−l
P
m=0
m!
0,1
0,2
0,3
0,4
0,5
06
0,90484
0,99532
0,99984
1,00000
0,81873
0,98248
0,99885
0,99994
1,00000
0,74081
0,96306
0,99640
0,99973
0,99998
1,00000
0,67032
0,93845
0,99207
0,99922
0,99994
1,00000
0,60653
0,90980
0,98561
0,99825
0,99982
1,00000
0,54881
0,80781
0,97688
0,99664
0,99960
1,00000
0,7
0,8
0,9
1,0
2,0
3,0
0,49658
0,84420
0,96586
0,99425
0,99921
0,99991
0,99999
1,00000
0,44933
0,80880
0,95258
0,99092
0,99859
0,99982
0,99998
1,00000
0,40657
0,77248
0,93714
0,98654
0,99766
0,99966
0,99996
1,00000
0,36790
0,73576
0,91970
0,98101
0,99634
0,99941
0,99992
1,00000
0,23534
0,40601
0,67668
0,85712
0,94735
0,98344
0,99547
0,99890
0,99976
0,99995
0,99999
0,04979
0,19915
0,42319
0,64723
0,81526
0,91600
0,96649
0,98810
0,99620
0,99890
0,99971
0,99993
0,99998
1,00000
ii
Т а б л. 2. (Окончание).
l
k
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
4,0
5,0
6,0
7,0
8,0
9,0
0,01832
0,09158
0,23810
0,43347
0,62883
0,78513
0,88933
0,94887
0,97864
0,99187
0,99716
0,99908
0,99973
0,99992
0,99998
0,99999
1,00000
0,00674
0,04042
0,12465
0,26503
0,44049
0,61596
0,76218
0,86662
0,93181
0,96817
0,98630
0,99455
0,99798
0,99920
0,99977
0,99993
0,99998
0,99999
1,00000
0,00248
0,01735
0,06197
0,15120
0,28506
0,44568
0,60630
0,74398
0,84724
0,91608
0,95738
0,97991
0,99117
0,99637
0,99860
0,99949
0,99982
0,99994
0,99998
0,99999
1,00000
0,00091
0,00730
0,02964
0,08176
0,17299
0,30071
0,44971
0,59871
0,72909
0,83050
0,90148
0,94665
0,97300
0,98719
0,99428
0,99759
0,99904
0,99964
0,99987
0,99995
0,99998
1,00000
0,00034
0,00302
0,01375
0,04238
0,09963
0,19124
0,31337
0,45296
0,59255
0,71662
0,81589
0,88808
0,93620
0,96582
0,98274
0,99177
0,99628
0,99841
0,99935
0,99974
0,99991
0,99997
0,99999
1,00000
0,00012
0,00123
0,00623
0,02123
0,05496
0,11569
0,20678
0,32390
0,45565
0,58741
0,70599
0,80301
0,87577
0,92615
0,95853
0,97796
0,98889
0,99468
0,99757
0,99894
0,99956
0,99982
0,99993
0,99997
0,99999
1,00000
iii
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2
2,1
2,2
x
0
0,3989
0,3970
0,3910
0,3814
0,3683
0,3521
0,3322
0,3123
0,2897
0,2661
0,2420
0,2179
0,1942
0,1714
0,1497
0,1295
0,1109
0,0940
0,0790
0,0656
0,0540
0,0440
0,0355
1
0,3989
0,3965
0,3902
0,3802
0,3668
0,3503
0,3312
0,3101
0,2874
0,2637
0,2396
0,2155
0,1919
0,1691
0,1476
0,1276
0,1092
0,0925
0,0775
0,0644
0,0529
0,0431
0,0347
2
0,3989
0,3961
0,3894
0,3790
0,3653
0,3485
0,3292
0,3079
0,2850
0,2613
0,2371
0,2131
0,1895
0,1669
0,1456
0,1257
0,1074
0,0909
0,0761
0,0632
0,0519
0,0422
0,0339
3
0,3988
0,3956
0,3885
0,3778
0,3637
0,3467
0,3271
0,3056
0,2827
0,2589
0,2347
0,2107
0,1872
0,1647
0,1435
0,1238
0,1057
0,0893
0,0748
0,0620
0,0508
0,0413
0,0332
сотые доли x
4
5
0,3986 0,3984
0,3951 0,3945
0,3876 0,3867
0,3765 0,3752
0,3621 0,3605
0,3448 0,3429
0,3251 0,3230
0,3034 0,3011
0,2803 0,2780
0,2565 0,2541
0,2323 0,2299
0,2083 0,2059
0,1849 0,1826
0,1626 0,1604
0,1415
0,1394
0,1219
0,1200
0,1040 0,1023
0,0878 0,0863
0,0734 0,0721
0,0608 0,0596
0,0498 0,0488
0,0404 0,0396
0,0325 0,0317
6
0,3982
0,3939
0,3857
0,3739
0,3589
0,3410
0,3209
0,2989
0,2756
0,2516
0,2275
0,2036
0,1804
0,1582
0,1374
0,1182
0,1006
0,0848
0,0707
0,0584
0,0478
0,0387
0,0310
7
0,3980
0,3932
0,3847
0,3725
0,3572
0,3391
0,3187
0,2966
0,2732
0,2492
0,2251
0,2012
0,1781
0,1561
0,1354
0,1163
0,0989
0,0833
0,0694
0,0573
0,0468
0,0379
0,0303
8
0,3977
0,3925
0,3836
0,3712
0,3555
0,3372
0,3166
0,2943
0,2709
0,2468
0,2227
0,1989
0,1758
0,1539
0,1334
0,1145
0,0973
0,0818
0,0681
0,0562
0,0459
0,0371
0,0297
9
0,3973
0,3918
0,3825
0,3697
0,3538
0,3352
0,3144
0,2920
0,2685
0,2444
0,2203
0,1965
0,1736
0,1518
0,1315
0,1127
0,957
0,0804
0,0669
0,0551
0,0449
0,0363
0,0290
1
2
Т а б л. 3. Значений функции w(x) = √ e−x /2
2p
iv
v
1,9
2
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
3
3,1
3,2
3,3
3,4
3,5
3,6
3,7
3,8
3,9
4
x
0
0,0656
0,0540
0,0440
0,0355
0,0283
0,0224
0,0175
0,0136
0,0104
0,0079
0,0060
0,0044
0,0033
0,0024
0,0017
0,0012
0,0009
0,0006
0,0004
0,0003
0,0002
0,0001
1
0,0644
0,0529
0,0431
0,0347
00277
0,0219
0,0171
0,0132
0,0101
0,0077
0,0058
0,0043
0,0032
0,0023
0,0017
0,0012
0,0008
0,0006
0,0004
0,0003
0,0002
0,0001
Т а б л. 3. (Продолжение).
2
0,0632
0,0519
0,0422
0,0339
0,0270
0,0213
0,0167
0,0129
0,0099
0,0075
0,0056
0,0042
0,0031
0,0022
0,0016
0,0012
0,0008
0,0006
0,0004
0,0003
0,0002
0,0001
3
0,0620
0,0508
0,0413
0,0332
0,0264
0,0208
0,0163
0,0126
0,0096
0,0073
0,0055
0,0040
0,0030
0,0022
0,0016
0,0011
0,0008
0,0005
0,0004
0,0003
0,0002
0,0001
сотые доли x
4
5
0,0608 0,0596
0,0498 0,0488
0,0404 0,0396
0,0325 0,0317
0,0258 0,0252
0,0203 0,0198
0,0158 0,0154
0,0122 0,0119
0,0093 0,0091
0,0071 0,0069
0,0053 0,0051
0,0039 0,0038
0,0029 0,0028
0,0021 0,0020
0,0015 0,0015
0,0011
0,0010
0,0008 0,0007
0,0005 0,0005
0,0004 0,0004
0,0003 0,0002
0,0002 0,0002
0,0001 0,0001
6
0,0584
0,0478
0,0387
0,0310
0,0246
0,0194
0,0151
0,0116
0,0088
0,0067
0,0050
0,0037
0,0027
0,0020
0,0014
0,0010
0,0007
0,0005
0,0003
0,0002
0,0002
0,0001
7
0,0573
0,0468
0,0379
0,0303
0,0241
0,0189
0,0147
0,0113
0,0086
0,0065
0,0048
0,0036
0,0026
0,0019
0,0014
0,0010
0,0007
0,0005
0,0003
0,0002
0,0002
0,0001
8
0,0562
0,0459
0,0371
0,0297
0,0235
0,0184
0,0143
0,0110
0,0084
0,0063
0,0047
0,0035
0,0025
0,0018
0,0013
0,0009
0,0007
0,0005
0,0003
0,0002
0,0001
0,0001
9
0,0551
0,0449
0,0363
0,0290
0,0229
0,0180
0,0139
0,0107
0,0081
0,0061
0,0046
0,0034
0,0025
0,0018
0,0013
0,0009
0,0006
0,0004
0,0003
0,0002
0,0001
0,0001
Т а б л. 4. Значения функции Лапласа F0 (x) = √
1 Rx −t 2 /2
e
dt
2p 0
x
F0 (x)
x
F0 (x)
x
F0 (x)
x
F0 (x)
0,00
0,01
0,02
0,03
0,04
0,05
0,06
0,07
0,08
0,09
0,1
0,11
0,12
0,13
0,14
0,15
0,16
0,17
0,18
0,19
0,2
0,21
0,22
0,23
0,24
0,25
0,26
0,27
0,28
0,29
0,3
0,31
0,32
0
0,004
0,008
0,012
0,016
0,0199
0,0239
0,0279
0,0319
0,0359
0,0398
0,0438
0,0478
0,0517
0,0557
0,0596
0,0636
0,0675
0,0714
0,0753
0,0793
0,0832
0,0871
0,091
0,0948
0,0987
0,1026
0,1064
0,1103
0,1141
0,1179
0,1217
0,1255
0,33
0,34
0,35
0,36
0,37
0,38
0,39
0,4
0,41
0,42
0,43
0,44
0,45
0,46
0,47
0,48
0,49
0,5
0,51
0,52
0,53
0,54
0,55
0,56
0,57
0,58
0,59
0,6
0,61
0,62
0,63
0,64
0,65
0,1293
0,1331
0,1368
0,1406
0,1443
0,148
0,1517
0,1554
0,1591
0,1628
0,1664
0,17
0,1736
0,1772
0,1808
0,1844
0,1879
0,1915
0,195
0,1985
0,2019
0,2054
0,2088
0,2123
0,2157
0,219
0,2224
0,2257
0,2291
0,2324
0,2357
0,2389
0,2422
0,66
0,67
0,68
0,69
0,7
0,71
0,72
0,73
0,74
0,75
0,76
0,77
0,78
0,79
0,8
0,81
0,82
0,83
0.84
0,85
0,86
0,87
0,88
0,89
0,9
0,91
0,92
0,93
0,94
0,95
0,96
0,97
0,98
0,2454
0,2486
0,2517
0,2549
0,258
0,2611
0,2642
0,2673
0.2703
0,2734
0,2764
0,2794
0,2823
0,2852
0,2881
0,291
0,2939
0,2967
0,2995
0,3023
0,3051
0,3078
0,3106
0,3133
0,3159
0,3186
0,3112
0,3238
0,3264
0,3289
0,3315
0,334
0,3365
0,99
1
1,01
1,02
1,03
1,04
1,05
1,06
1,07
1,08
1,09
1,1
1,11
1,12
1,13
1,14
1,15
1,16
1,17
1,18
1,19
1,2
1,21
1,22
1,23
1,24
1,25
1,26
1,27
1,28
1,29
1,3
1,31
0,3389
0,3413
0,3438
0,3461
0,3485
0,3508
0,3531
0,3554
0,3577
0,3599
0,3621
0,3643
0,3665
0,3686
0,3708
0,3729
0,3749
0,377
0,379
0,381
0,383
0,3849
0,3869
0,3888
0,3907
0,3925
0,3914
0,3962
0,398
0,3997
0,4015
0,4032
0,4049
vi
Т а б л. 4. (Окончание).
x
F0 (x)
x
F0 (x)
x
F0 (x)
x
F0 (x)
1,32
1,33
1,34
1,35
1,36
1,37
1,38
1,39
1,4
1,41
1,42
1,43
1,44
1,45
1,46
1,47
1,48
1,49
1,5
1,51
1,52
1,53
1,54
1,55
1,56
1,57
1,58
1,59
1,6
1,61
1,62
1,63
0,4066
0,4082
0,4099
0,4115
0,4131
0,4147
0,4162
0,4177
0,4192
0,4207
0,4222
0,4236
0,4251
0,4265
0,4279
0,4292
0,4306
0,4319
0,4332
0,4345
0,4357
0,437
0,4382
0,4394
0,4406
0,4418
0,4429
0,4441
0,4452
0,4463
0,4474
0,4484
1,64
1,65
1,66
1,67
1,68
1,69
1,7
1,71
1,72
1,73
1,74
1,75
1,76
1,77
1,78
1,79
1,8
1,81
1,82
1,83
1,84
1,85
1,86
1,87
1,88
1,89
1,9
1,91
1,92
1,93
1,94
1,95
0,4495
0,4505
0,4515
0,4525
0,4535
0,4545
0,4554
0,4564
0,4573
0,4582
0,4591
0,4599
0,4608
0,4616
0,4625
0,4633
0,4641
0,4649
0,4656
0,4664
0,4671
0,4678
0,4686
0,4693
0,4699
0,4706
0,4713
0,4719
0,4726
0,4732
0,4738
0,4744
1,96
1,97
1,98
1,99
2
2,02
2,04
2,06
2,08
2,1
2,12
2,14
2,16
2,18
2,2
2,22
2,24
2,26
2,28
2,3
2,32
2,34
2,36
2,38
2,4
2,42
2,44
2,46
2,48
2,5
2,52
2,54
0,475
0,4756
0,4761
0,4767
0,4772
0,4783
0,4793
0,4803
0,4812
0,4821
0,483
0,4838
0,4846
4854
0,4861
0,4868
0,4875
0,4881
0,4887
0,4893
0,4898
0,4904
0,4908
0,4913
0,4918
0,4922
0,4927
0,4931
0,4934
0,4938
0,4941
0,4945
2,56
2,58
2,6
2,62
2,64
2,66
2,68
2,7
2,72
2,74
2,76
2,78
2,8
2,82
2,84
2,86
2,88
2,9
2,92
2,94
2,96
2,98
3
3,2
3,4
3,6
3,8
4
4,5
5
0,4948
0,4951
0,4953
0,4956
0,4959
0,4961
0,4963
0,4965
0,4967
0,4969
0,4971
0,4973
0,4974
0,4976
0,4977
0,4979
0,498
0,4981
0,4982
0,4984
0,4985
0,4986
0,49865
0,49931
0,49966
0,499841
0,499928
0,499968
0,499997
0,5
vii
Т а б л. 5. t-распределение. В таблице приведены значения точек xдля величины
tn с распределением Стьюдента с n степенями свободы такие, что
P{|tn | > x} = a, a в верхней строке, или P{tn > x} = a, a в нижней строке.
a
0,20
0,1
0,05
0,02
0,01
0,001
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
∞
3,077684 6,313752 12,70620 31,82052 63,65674 636,6192
1,885618
2,919986 4,30265
6,96456
9,92484
31,5991
1,637744 2,353363 3,18245
4,54070
5,84091
12,9240
1,533206 2,131847
2,77645
3,74695
4,60409
8,6103
1,475884 2,015048 2,57058
3,36493
4,03214
6,8688
1,439756 1,943180
2,44691
3,14267
3,70743
5,9588
1,414924
1,894579 2,36462
2,99795
3,49948
5,4079
1,396815
1,859548 2,30600
2,89646
3,35539
5,0413
1,383029 1,833113
2,26216
2,82144
3,24984
4,7809
1,372184
1,812461
2,22814
2,76377
3,16927
4,5869
1,363430 1,795885 2,20099
2,71808
3,10581
4,4370
1,356217
1,782288 2,17881
2,68100
3,05454
4,3178
1,350171
1,770933 2,16037
2,65031
3,01228
4,2208
1,345030 1,761310
2,14479
2,62449
2,97684
4,1405
1,340606 1,753050 2,13145
2,60248
2,94671
4,0728
1,336757 1,745884 2,11991
2,58349
2,92078
4,0150
1,333379 1,739607 2,10982
2,56693
2,89823
3,9651
1,330391
1,734064 2,10092
2,55238
2,87844
3,9216
1,327728 1,729133
2,09302
2,53948
2,86093
3,8834
1,325341
1,724718
2,08596
2,52798
2,84534
3,8495
1,323188
1,720743 2,07961
2,51765
2,83136
3,8193
1,321237
1,717144
2,07387
2,50832
2,81876
3,7921
1,319460
1,713872
2,06866
2,49987
2,80734
3,7676
1,317836
1,710882
2,06390
2,49216
2,79694
3,7454
1,316345
1,708141
2,05954
2,48511
2,78744
3,7251
1,314972
1,705618
2,05553
2,47863
2,77871
3,7066
1,313703
1,703288 2,05183
2,47266
2,77068
3,6896
1,312527
1,701131
2,04841
2,46714
2,76326
3,6739
1,311434
1,699127
2,04523
2,46202
2,75639
3,6594
1,310415
1,697261
2,04227
2,45726
2,75000
3,6460
1,281552
1,644854 1,95996
2,32635
2,57583
3,2905
0,10
0,05
0,025
0,01
0,005
0,0005
Уровень значимости a для односторонней критической области
viii
Т а б л. 6. Распределение x2 (n). Значения x2p,n :
x2p,n
p=
p
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
R
0
kn (x)dx =
x2p,n
1
2n/2 G(n/2)
·
R
xn/2−1 e−x/2 dx
0
0,01
0,025
0,05
0,95
0,975
0,99
0,00016
0,02010
0,11483
0,29711
0,55430
0,87209
1,23904
1,64650
2,08790
2,55821
3,05348
3,57057
4,10692
4,66043
5,22935
5,81221
6,40776
7,01491
7,63273
8,26040
8,89720
9,54249
10,19572
10,85636
11,52398
12,19815
12,87850
13,56471
14,25645
14,95346
0,00098
0,05064
0,21580
0,48442
0,83121
1,23734
1,68987
2,17973
2,70039
3,24697
3,81575
4,40379
5,00875
5,62873
6,26214
6,90766
7,56419
8,23075
8,90652
9,59078
10,28290
10,98232
11,68855
12,40115
13,11972
13,84390
14,57338
15,30786
16,04707
16,79077
0,00393
0,10259
0,35185
0,71072
1,14548
1,63538
2,16735
2,73264
3,32511
3,94030
4,57481
5,22603
5,89186
6,57063
7,26094
7,96165
8,67176
9,39046
10,11701
10,85081
11,59131
12,33801
13,09051
13,84843
14,61141
15,37916
16,15140
16,92788
17,70837
18,49266
3,84146
5,99146
7,81473
9,48773
11,07050
12,59159
14,06714
15,50731
16,91898
18,30704
19,67514
21,02607
22,36203
23,68479
24,99579
26,29623
27,58711
28,86930
30,14353
31,41043
32,67057
33,92444
35,17246
36,41503
37,65248
38,88514
40,11327
41,33714
42,55697
43,77297
5,02389
7,37776
9,34840
11,14329
12,83250
14,44938
16,01276
17,53455
19,02277
20,48318
21,92005
23,33666
24,73560
26,11895
27,48839
28,84535
30,19101
31,52638
32,85233
34,16961
35,47888
36,78071
38,07563
39,36408
40,64647
41,92317
43,19451
44,46079
45,72229
46,97924
6,63490
9,21034
11,34487
13,27670
15,08627
16,81189
18,47531
20,09024
21,66599
23,20925
24,72497
26,21697
27,68825
29,14124
30,57791
31,99993
33,40866
34,80531
36,19087
37,56623
38,93217
40,28936
41,63840
42,97982
44,31410
45,64168
46,96294
48,27824
49,58788
50,89218
ix
p
Т а б л. 7. Критерий Колмогорова
значения функции l p : p = P(Dn =
= sup |Fn (x) − F (x)| > l p ) →
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
25
30
35
40
45
50
55
60
65
70
75
80
85
90
95
100
x
Т а б л. 6. Окончание
p
n
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
0.999
0,9999
6,63
9,21
11,3
13,3
15,1
16,8
18,5
20,1
21,7
23,2
24,7
26,2
20,1
29,1
30,6
32,0
33,4
34,8
36,2
37,6
38,9
40,3
41,6
43,0
44,3
45,6
47,0
48,3
49,6
50,9
10,8
13,8
16,3
18,5
20,5
22,5
24,3
26,1
27,9
29,6
31,3
32,9
26,1
36,1
37,7
39,3
40,8
42,3
43,8
45,3
46,8
48,3
49,7
51,2
52,6
54,1
55,5
56,9
58,3
59,7
x
0,10
0,05
0,01
0,950
0,776
0,636
0,565
0,509
0,468
0,436
0,410
0,387
0,369
0,352
0,338
0,325
0,314
0,304
0,295
0,286
0,279
0,271
0,265
0,238
0,218
0,202
0,189
0,179
0,170
0,162
0,155
0,149
0,144
0,139
0,135
0,131
0,127
0,124
0,121
0,975
0,842
0,708
0,624
0,563
0,519
0,483
0,454
0,430
0,409
0,391
0,375
0,361
0,349
0,338
0,327
0,318
0,309
0,301
0,294
0,264
0,242
0,224
0,210
0,198
0,188
0,180
0,172
0,166
0,160
0,154
0,150
0,145
0,141
0,137
0,134
0,995
0,929
0,829
0,734
0,669
0,617
0,576
0,542
0,513
0,489
0,468
0,449
0,432
0,418
0,404
0,392
0,381
0,371
0,361
0,352
0,317
0,290
0,269
0,252
0,238
0,226
0,216
0,207
0,199
0,192
0,185
0,179
0,174
0,169
0,165
0,161
F-распредел m, n —число степеней свободы (n—больш. дисперсия)
Т а б л. 8. F-распределение для a = 0, 1.
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
1
2
3
4
5
6
39,86346
8,52632
5,53832
4,54477
4,06042
3,77595
3,58943
3,45792
3,36030
3,28502
3,22520
3,17655
3,13621
3,10221
3,07319
3,04811
3,02623
3,00698
2,98990
2,97465
2,96096
2,94858
2,93736
2,92712
2,91774
2,90913
2,90119
2,89385
2,88703
2,88069
2,83535
2,79107
2,74781
2,70554
49,50000
9,00000
5,46238
4,32456
3,77972
3,46330
3,25744
3,11312
3,00645
2,92447
2,85951
2,80680
2,76317
2,72647
2,69517
2,66817
2,64464
2,62395
2,60561
2,58925
2,57457
2,56131
2,54929
2,53833
2,52831
2,51910
2,51061
2,50276
2,49548
2,48872
2,44037
2,39325
2,34734
2,30259
53,59324
9,16179
5,39077
4,19086
3,61948
3,28876
3,07407
2,92380
2,81286
2,72767
2,66023
2,60552
2,56027
2,52222
2,48979
2,46181
2,43743
2,41601
2,39702
2,38009
2,36489
2,35117
2,33873
2,32739
2,31702
2,30749
2,29871
2,29060
2,28307
2,27607
2,22609
2,17741
2,12999
2,08380
55,83296
9,24342
5,34264
4,10725
3,52020
3,18076
2,96053
2,80643
2,69268
2,60534
2,53619
2,48010
2,43371
2,39469
2,36143
2,33274
2,30775
2,28577
2,26630
2,24893
2,23334
2,21927
2,20651
2,19488
2,18424
2,17447
2,16546
2,15714
2,14941
2,14223
2,09095
2,04099
1,99230
1,94486
57,24008
9,29263
5,30916
4,05058
3,45298
3,10751
2,88334
2,72645
2,61061
2,52164
2,45118
2,39402
2,34672
2,30694
2,27302
2,24376
2,21825
2,19583
2,17596
2,15823
2,14231
2,12794
2,11491
2,10303
2,09216
2,08218
2,07298
2,06447
2,05658
2,04925
1,99682
1,94571
1,89587
1,84727
58,20442
9,32553
5,28473
4,00975
3,40451
3,05455
2,82739
2,66833
2,55086
2,46058
2,38907
2,33102
2,28298
2,24256
2,20808
2,17833
2,15239
2,12958
2,10936
2,09132
2,07512
2,06050
2,04723
2,03513
2,02406
2,01389
2,00452
1,99585
1,98781
1,98033
1,92688
1,87472
1,82381
1,77411
xi
Т а б л. 8 (Продолжение).
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
7
8
9
10
12
15
58,90595
9,34908
5,26619
3,97897
3,36790
3,01446
2,78493
2,62413
2,50531
2,41397
2,34157
2,28278
2,23410
2,19313
2,15818
2,12800
2,10169
2,07854
2,05802
2,03970
2,02325
2,00840
1,99492
1,98263
1,97138
1,96104
1,95151
1,94270
1,93452
1,92692
1,87252
1,81939
1,76748
1,71672
59,43898
9,36677
5,25167
3,95494
3,33928
2,98304
2,75158
2,58935
2,46941
2,37715
2,30400
2,24457
2,19535
2,15390
2,11853
2,08798
2,06134
2,03789
2,01710
1,99853
1,98186
1,96680
1,95312
1,94066
1,92925
1,91876
1,90909
1,90014
1,89184
1,88412
1,82886
1,77483
1,72196
1,67020
59,85759
9,38054
5,24000
3,93567
3,31628
2,95774
2,72468
2,56124
2,44034
2,34731
2,27350
2,21352
2,16382
2,12195
2,08621
2,05533
2,02839
2,00467
1,98364
1,96485
1,94797
1,93273
1,91888
1,90625
1,89469
1,88407
1,87427
1,86520
1,85679
1,84896
1,79290
1,73802
1,68425
1,63152
60,19498
9,39157
5,23041
3,91988
3,29740
2,93693
2,70251
2,53804
2,41632
2,32260
2,24823
2,18776
2,13763
2,09540
2,05932
2,02815
2,00094
1,97698
1,95573
1,93674
1,91967
1,90425
1,89025
1,87748
1,86578
1,85503
1,84511
1,83593
1,82741
1,81949
1,76269
1,70701
1,65238
1,59872
60,70521
9,40813
5,21562
3,89553
3,26824
2,90472
2,66811
2,50196
2,37888
2,28405
2,20873
2,14744
2,09659
2,05371
2,01707
1,98539
1,95772
1,93334
1,91170
1,89236
1,87497
1,85925
1,84497
1,83194
1,82000
1,80902
1,79889
1,78951
1,78081
1,77270
1,71456
1,65743
1,60120
1,54578
61,22034
9,42471
5,20031
3,87036
3,23801
2,87122
2,63223
2,46422
2,33962
2,24351
2,16709
2,10485
2,05316
2,00953
1,97222
1,93992
1,91169
1,88681
1,86471
1,84494
1,82715
1,81106
1,79643
1,78308
1,77083
1,75957
1,74917
1,73954
1,73060
1,72227
1,66241
1,60337
1,54500
1,48714
xii
Т а б л. 8 (Окончание)
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
20
24
30
40
60
120
61,74029
9,44131
5,18448
3,84434
3,20665
2,83634
2,59473
2,42464
2,29832
2,20074
2,12305
2,05968
2,00698
1,96245
1,92431
1,89127
1,86236
1,83685
1,81416
1,79384
1,77555
1,75899
1,74392
1,73015
1,71752
1,70589
1,69514
1,68519
1,67593
1,66731
1,60515
1,54349
1,48207
1,42060
62,00205
9,44962
5,17636
3,83099
3,19052
2,81834
2,57533
2,40410
2,27683
2,17843
2,10001
2,03599
1,98272
1,93766
1,89904
1,86556
1,83624
1,81035
1,78731
1,76667
1,74807
1,73122
1,71588
1,70185
1,68898
1,67712
1,66616
1,65600
1,64655
1,63774
1,57411
1,51072
1,44723
1,38318
62,26497
9,45793
5,16811
3,81742
3,17408
2,79996
2,55546
2,38302
2,25472
2,15543
2,07621
2,01149
1,95757
1,91193
1,87277
1,83879
1,80901
1,78269
1,75924
1,73822
1,71927
1,70208
1,68643
1,67210
1,65895
1,64682
1,63560
1,62519
1,61551
1,60648
1,54108
1,47554
1,40938
1,34187
62,52905
9,46624
5,15972
3,80361
3,15732
2,78117
2,53510
2,36136
2,23196
2,13169
2,05161
1,98610
1,93147
1,88516
1,84539
1,81084
1,78053
1,75371
1,72979
1,70833
1,68896
1,67138
1,65535
1,64067
1,62718
1,61472
1,60320
1,59250
1,58253
1,57323
1,50562
1,43734
1,36760
1,29513
62,79428
9,47456
5,15119
3,78957
3,14023
2,76195
2,51422
2,33910
2,20849
2,10716
2,02612
1,95973
1,90429
1,85723
1,81676
1,78156
1,75063
1,72322
1,69876
1,67678
1,65691
1,63885
1,62237
1,60726
1,59335
1,58050
1,56859
1,55753
1,54721
1,53757
1,46716
1,39520
1,32034
1,23995
63,06064
9,48289
5,14251
3,77527
3,12279
2,74229
2,49279
2,31618
2,18427
2,08176
1,99965
1,93228
1,87591
1,82800
1,78672
1,75075
1,71909
1,69099
1,66587
1,64326
1,62278
1,60415
1,58711
1,57146
1,55703
1,54368
1,53129
1,51976
1,50899
1,49891
1,42476
1,34757
1,26457
1,16860
xiii
Т а б л. 9. F-распределение для a = 0, 05.
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
2
3
4
5
6
7
199,5000
19,0000
9,5521
6,9443
5,7861
5,1433
4,7374
4,4590
4,2565
4,1028
3,9823
3,8853
3,8056
3,7389
3,6823
3,6337
3,5915
3,5546
3,5219
3,4928
3,4668
3,4434
3,4221
3,4028
3,3852
3,3690
3,3541
3,3404
3,3277
3,3158
3,2317
3,1504
3,0718
2,9957
215,7073
19,1643
9,2766
6,5914
5,4095
4,7571
4,3468
4,0662
3,8625
3,7083
3,5874
3,4903
3,4105
3,3439
3,2874
3,2389
3,1968
3,1599
3,1274
3,0984
3,0725
3,0491
3,0280
3,0088
2,9912
2,9752
2,9604
2,9467
2,9340
2,9223
2,8387
2,7581
2,6802
2,6049
224,5832
19,2468
9,1172
6,3882
5,1922
4,5337
4,1203
3,8379
3,6331
3,4780
3,3567
3,2592
3,1791
3,1122
3,0556
3,0069
2,9647
2,9277
2,8951
2,8661
2,8401
2,8167
2,7955
2,7763
2,7587
2,7426
2,7278
2,7141
2,7014
2,6896
2,6060
2,5252
2,4472
2,3719
230,1619
19,2964
9,0135
6,2561
5,0503
4,3874
3,9715
3,6875
3,4817
3,3258
3,2039
3,1059
3,0254
2,9582
2,9013
2,8524
2,8100
2,7729
2,7401
2,7109
2,6848
2,6613
2,6400
2,6207
2,6030
2,5868
2,5719
2,5581
2,5454
2,5336
2,4495
2,3683
2,2899
2,2141
233,9860
19,3295
8,9406
6,1631
4,9503
4,2839
3,8660
3,5806
3,3738
3,2172
3,0946
2,9961
2,9153
2,8477
2,7905
2,7413
2,6987
2,6613
2,6283
2,5990
2,5727
2,5491
2,5277
2,5082
2,4904
2,4741
2,4591
2,4453
2,4324
2,4205
2,3359
2,2541
2,1750
2,0986
236,7684
19,3532
8,8867
6,0942
4,8759
4,2067
3,7870
3,5005
3,2927
3,1355
3,0123
2,9134
2,8321
2,7642
2,7066
2,6572
2,6143
2,5767
2,5435
2,5140
2,4876
2,4638
2,4422
2,4226
2,4047
2,3883
2,3732
2,3593
2,3463
2,3343
2,2490
2,1665
2,0868
2,0096
xiv
Т а б л. 9. (Продолжение)
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
8
9
10
12
15
20
238,8827
19,3710
8,8452
6,0410
4,8183
4,1468
3,7257
3,4381
3,2296
3,0717
2,9480
2,8486
2,7669
2,6987
2,6408
2,5911
2,5480
2,5102
2,4768
2,4471
2,4205
2,3965
2,3748
2,3551
2,3371
2,3205
2,3053
2,2913
2,2783
2,2662
2,1802
2,0970
2,0164
1,9384
240,5433
19,3848
8,8123
5,9988
4,7725
4,0990
3,6767
3,3881
3,1789
3,0204
2,8962
2,7964
2,7144
2,6458
2,5876
2,5377
2,4943
2,4563
2,4227
2,3928
2,3660
2,3419
2,3201
2,3002
2,2821
2,2655
2,2501
2,2360
2,2229
2,2107
2,1240
2,0401
1,9588
1,8799
241,8817
19,3959
8,7855
5,9644
4,7351
4,0600
3,6365
3,3472
3,1373
2,9782
2,8536
2,7534
2,6710
2,6022
2,5437
2,4935
2,4499
2,4117
2,3779
2,3479
2,3210
2,2967
2,2747
2,2547
2,2365
2,2197
2,2043
2,1900
2,1768
2,1646
2,0772
1,9926
1,9105
1,8307
243,9060
19,4125
8,7446
5,9117
4,6777
3,9999
3,5747
3,2839
3,0729
2,9130
2,7876
2,6866
2,6037
2,5342
2,4753
2,4247
2,3807
2,3421
2,3080
2,2776
2,2504
2,2258
2,2036
2,1834
2,1649
2,1479
2,1323
2,1179
2,1045
2,0921
2,0035
1,9174
1,8337
1,7522
245,9499
19,4291
8,7029
5,8578
4,6188
3,9381
3,5107
3,2184
3,0061
2,8450
2,7186
2,6169
2,5331
2,4630
2,4034
2,3522
2,3077
2,2686
2,2341
2,2033
2,1757
2,1508
2,1282
2,1077
2,0889
2,0716
2,0558
2,0411
2,0275
2,0148
1,9245
1,8364
1,7505
1,6664
248,0131
19,4458
8,6602
5,8025
4,5581
3,8742
3,4445
3,1503
2,9365
2,7740
2,6464
2,5436
2,4589
2,3879
2,3275
2,2756
2,2304
2,1906
2,1555
2,1242
2,0960
2,0707
2,0476
2,0267
2,0075
1,9898
1,9736
1,9586
1,9446
1,9317
1,8389
1,7480
1,6587
1,5705
xv
Т а б л. 9 (Окончание)
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
24
30
40
60
120
∞
249,0518
19,4541
8,6385
5,7744
4,5272
3,8415
3,4105
3,1152
2,9005
2,7372
2,6090
2,5055
2,4202
2,3487
2,2878
2,2354
2,1898
2,1497
2,1141
2,0825
2,0540
2,0283
2,0050
1,9838
1,9643
1,9464
1,9299
1,9147
1,9005
1,8874
1,7929
1,7001
1,6084
1,5173
250,0951
19,4624
8,6166
5,7459
4,4957
3,8082
3,3758
3,0794
2,8637
2,6996
2,5705
2,4663
2,3803
2,3082
2,2468
2,1938
2,1477
2,1071
2,0712
2,0391
2,0102
1,9842
1,9605
1,9390
1,9192
1,9010
1,8842
1,8687
1,8543
1,8409
1,7444
1,6491
1,5543
1,4591
251,1432
19,4707
8,5944
5,7170
4,4638
3,7743
3,3404
3,0428
2,8259
2,6609
2,5309
2,4259
2,3392
2,2664
2,2043
2,1507
2,1040
2,0629
2,0264
1,9938
1,9645
1,9380
1,9139
1,8920
1,8718
1,8533
1,8361
1,8203
1,8055
1,7918
1,6928
1,5943
1,4952
1,3940
252,1957
19,4791
8,5720
5,6877
4,4314
3,7398
3,3043
3,0053
2,7872
2,6211
2,4901
2,3842
2,2966
2,2229
2,1601
2,1058
2,0584
2,0166
1,9795
1,9464
1,9165
1,8894
1,8648
1,8424
1,8217
1,8027
1,7851
1,7689
1,7537
1,7396
1,6373
1,5343
1,4290
1,3180
253,2529
19,4874
8,5494
5,6581
4,3985
3,7047
3,2674
2,9669
2,7475
2,5801
2,4480
2,3410
2,2524
2,1778
2,1141
2,0589
2,0107
1,9681
1,9302
1,8963
1,8657
1,8380
1,8128
1,7896
1,7684
1,7488
1,7306
1,7138
1,6981
1,6835
1,5766
1,4673
1,3519
1,2214
254,3144
19,4957
8,5264
5,6281
4,3650
3,6689
3,2298
2,9276
2,7067
2,5379
2,4045
2,2962
2,2064
2,1307
2,0658
2,0096
1,9604
1,9168
1,8780
1,8432
1,8117
1,7831
1,7570
1,7330
1,7110
1,6906
1,6717
1,6541
1,6376
1,6223
1,5089
1,3893
1,2539
1,0000
xvi
Т а б л. 10. F-распределение для a = 0, 025.
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
2
3
4
5
6
7
799,5000
39,0000
16,0441
10,6491
8,4336
7,2599
6,5415
6,0595
5,7147
5,4564
5,2559
5,0959
4,9653
4,8567
4,7650
4,6867
4,6189
4,5597
4,5075
4,4613
4,4199
4,3828
4,3492
4,3187
4,2909
4,2655
4,2421
4,2205
4,2006
4,1821
4,0510
3,9253
3,8046
3,6889
864,1630
39,1655
15,4392
9,9792
7,7636
6,5988
5,8898
5,4160
5,0781
4,8256
4,6300
4,4742
4,3472
4,2417
4,1528
4,0768
4,0112
3,9539
3,9034
3,8587
3,8188
3,7829
3,7505
3,7211
3,6943
3,6697
3,6472
3,6264
3,6072
3,5894
3,4633
3,3425
3,2269
3,1161
899,5833
39,2484
15,1010
9,6045
7,3879
6,2272
5,5226
5,0526
4,7181
4,4683
4,2751
4,1212
3,9959
3,8919
3,8043
3,7294
3,6648
3,6083
3,5587
3,5147
3,4754
3,4401
3,4083
3,3794
3,3530
3,3289
3,3067
3,2863
3,2674
3,2499
3,1261
3,0077
2,8943
2,7858
921,8479
39,2982
14,8848
9,3645
7,1464
5,9876
5,2852
4,8173
4,4844
4,2361
4,0440
3,8911
3,7667
3,6634
3,5764
3,5021
3,4379
3,3820
3,3327
3,2891
3,2501
3,2151
3,1835
3,1548
3,1287
3,1048
3,0828
3,0626
3,0438
3,0265
2,9037
2,7863
2,6740
2,5665
937,1111
39,3315
14,7347
9,1973
6,9777
5,8198
5,1186
4,6517
4,3197
4,0721
3,8807
3,7283
3,6043
3,5014
3,4147
3,3406
3,2767
3,2209
3,1718
3,1283
3,0895
3,0546
3,0232
2,9946
2,9685
2,9447
2,9228
2,9027
2,8840
2,8667
2,7444
2,6274
2,5154
2,4082
948,2169
39,3552
14,6244
9,0741
6,8531
5,6955
4,9949
4,5286
4,1970
3,9498
3,7586
3,6065
3,4827
3,3799
3,2934
3,2194
3,1556
3,0999
3,0509
3,0074
2,9686
2,9338
2,9023
2,8738
2,8478
2,8240
2,8021
2,7820
2,7633
2,7460
2,6238
2,5068
2,3948
2,2875
xvii
Т а б л. 10. (Продолжение)
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
8
9
10
12
15
20
956,6562
39,3730
14,5399
8,9796
6,7572
5,5996
4,8993
4,4333
4,1020
3,8549
3,6638
3,5118
3,3880
3,2853
3,1987
3,1248
3,0610
3,0053
2,9563
2,9128
2,8740
2,8392
2,8077
2,7791
2,7531
2,7293
2,7074
2,6872
2,6686
2,6513
2,5289
2,4117
2,2994
2,1918
963,2846
39,3869
14,4731
8,9047
6,6811
5,5234
4,8232
4,3572
4,0260
3,7790
3,5879
3,4358
3,3120
3,2093
3,1227
3,0488
2,9849
2,9291
2,8801
2,8365
2,7977
2,7628
2,7313
2,7027
2,6766
2,6528
2,6309
2,6106
2,5919
2,5746
2,4519
2,3344
2,2217
2,1136
968,6274
39,3980
14,4189
8,8439
6,6192
5,4613
4,7611
4,2951
3,9639
3,7168
3,5257
3,3736
3,2497
3,1469
3,0602
2,9862
2,9222
2,8664
2,8172
2,7737
2,7348
2,6998
2,6682
2,6396
2,6135
2,5896
2,5676
2,5473
2,5286
2,5112
2,3882
2,2702
2,1570
2,0483
976,7079
39,4146
14,3366
8,7512
6,5245
5,3662
4,6658
4,1997
3,8682
3,6209
3,4296
3,2773
3,1532
3,0502
2,9633
2,8890
2,8249
2,7689
2,7196
2,6758
2,6368
2,6017
2,5699
2,5411
2,5149
2,4908
2,4688
2,4484
2,4295
2,4120
2,2882
2,1692
2,0548
1,9447
984,8668
39,4313
14,2527
8,6565
6,4277
5,2687
4,5678
4,1012
3,7694
3,5217
3,3299
3,1772
3,0527
2,9493
2,8621
2,7875
2,7230
2,6667
2,6171
2,5731
2,5338
2,4984
2,4665
2,4374
2,4110
2,3867
2,3644
2,3438
2,3248
2,3072
2,1819
2,0613
1,9450
1,8326
993,1028
39,4479
14,1674
8,5599
6,3286
5,1684
4,4667
3,9995
3,6669
3,4185
3,2261
3,0728
2,9477
2,8437
2,7559
2,6808
2,6158
2,5590
2,5089
2,4645
2,4247
2,3890
2,3567
2,3273
2,3005
2,2759
2,2533
2,2324
2,2131
2,1952
2,0677
1,9445
1,8249
1,7085
xviii
Т а б л. 10. (Окончание)
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
24
30
40
60
120
∞
997,2492
39,4562
14,1241
8,5109
6,2780
5,1172
4,4150
3,9472
3,6142
3,3654
3,1725
3,0187
2,8932
2,7888
2,7006
2,6252
2,5598
2,5027
2,4523
2,4076
2,3675
2,3315
2,2989
2,2693
2,2422
2,2174
2,1946
2,1735
2,1540
2,1359
2,0069
1,8817
1,7597
1,6402
1001,414
39,465
14,081
8,461
6,227
5,065
4,362
3,894
3,560
3,311
3,118
2,963
2,837
2,732
2,644
2,568
2,502
2,445
2,394
2,349
2,308
2,272
2,239
2,209
2,182
2,157
2,133
2,112
2,092
2,074
1,943
1,815
1,690
1,566
1005,598
39,473
14,037
8,411
6,175
5,012
4,309
3,840
3,505
3,255
3,061
2,906
2,780
2,674
2,585
2,509
2,442
2,384
2,333
2,287
2,246
2,210
2,176
2,146
2,118
2,093
2,069
2,048
2,028
2,009
1,875
1,744
1,614
1,484
1009,800
39,481
13,992
8,360
6,123
4,959
4,254
3,784
3,449
3,198
3,004
2,848
2,720
2,614
2,524
2,447
2,380
2,321
2,270
2,223
2,182
2,145
2,111
2,080
2,052
2,026
2,002
1,980
1,959
1,940
1,803
1,667
1,530
1,388
1014,020
39,490
13,947
8,309
6,069
4,904
4,199
3,728
3,392
3,140
2,944
2,787
2,659
2,552
2,461
2,383
2,315
2,256
2,203
2,156
2,114
2,076
2,041
2,010
1,981
1,954
1,930
1,907
1,886
1,866
1,724
1,581
1,433
1,268
1018,258
39,498
13,902
8,257
6,015
4,849
4,142
3,670
3,333
3,080
2,883
2,725
2,595
2,487
2,395
2,316
2,247
2,187
2,133
2,085
2,042
2,003
1,968
1,935
1,906
1,878
1,853
1,829
1,807
1,787
1,637
1,482
1,310
1,000
xix
Т а б л. 11. F-распределение для a = 0, 01.
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
1
2
3
4
5
6
4052,181
98,503
34,116
21,198
16,258
13,745
12,246
11,259
10,561
10,044
9,646
9,330
9,074
8,862
8,683
8,531
8,400
8,285
8,185
8,096
8,017
7,945
7,881
7,823
7,770
7,721
7,677
7,636
7,598
7,562
7,314
7,077
6,851
6,635
4999,500
99,000
30,817
18,000
13,274
10,925
9,547
8,649
8,022
7,559
7,206
6,927
6,701
6,515
6,359
6,226
6,112
6,013
5,926
5,849
5,780
5,719
5,664
5,614
5,568
5,526
5,488
5,453
5,420
5,390
5,179
4,977
4,787
4,605
5403,352
99,166
29,457
16,694
12,060
9,780
8,451
7,591
6,992
6,552
6,217
5,953
5,739
5,564
5,417
5,292
5,185
5,092
5,010
4,938
4,874
4,817
4,765
4,718
4,675
4,637
4,601
4,568
4,538
4,510
4,313
4,126
3,949
3,782
5624,583
99,249
28,710
15,977
11,392
9,148
7,847
7,006
6,422
5,994
5,668
5,412
5,205
5,035
4,893
4,773
4,669
4,579
4,500
4,431
4,369
4,313
4,264
4,218
4,177
4,140
4,106
4,074
4,045
4,018
3,828
3,649
3,480
3,319
5763,650
99,299
28,237
15,522
10,967
8,746
7,460
6,632
6,057
5,636
5,316
5,064
4,862
4,695
4,556
4,437
4,336
4,248
4,171
4,103
4,042
3,988
3,939
3,895
3,855
3,818
3,785
3,754
3,725
3,699
3,514
3,339
3,174
3,017
5858,986
99,333
27,911
15,207
10,672
8,466
7,191
6,371
5,802
5,386
5,069
4,821
4,620
4,456
4,318
4,202
4,102
4,015
3,939
3,871
3,812
3,758
3,710
3,667
3,627
3,591
3,558
3,528
3,499
3,473
3,291
3,119
2,956
2,802
xx
Т а б л. 11. (Продолжение)
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
7
8
9
10
12
15
5928,356
99,356
27,672
14,976
10,456
8,260
6,993
6,178
5,613
5,200
4,886
4,640
4,441
4,278
4,142
4,026
3,927
3,841
3,765
3,699
3,640
3,587
3,539
3,496
3,457
3,421
3,388
3,358
3,330
3,304
3,124
2,953
2,792
2,639
5981,070
99,374
27,489
14,799
10,289
8,102
6,840
6,029
5,467
5,057
4,744
4,499
4,302
4,140
4,004
3,890
3,791
3,705
3,631
3,564
3,506
3,453
3,406
3,363
3,324
3,288
3,256
3,226
3,198
3,173
2,993
2,823
2,663
2,511
6022,473
99,388
27,345
14,659
10,158
7,976
6,719
5,911
5,351
4,942
4,632
4,388
4,191
4,030
3,895
3,780
3,682
3,597
3,523
3,457
3,398
3,346
3,299
3,256
3,217
3,182
3,149
3,120
3,092
3,067
2,888
2,718
2,559
2,407
6055,847
99,399
27,229
14,546
10,051
7,874
6,620
5,814
5,257
4,849
4,539
4,296
4,100
3,939
3,805
3,691
3,593
3,508
3,434
3,368
3,310
3,258
3,211
3,168
3,129
3,094
3,062
3,032
3,005
2,979
2,801
2,632
2,472
2,321
6106,321
99,416
27,052
14,374
9,888
7,718
6,469
5,667
5,111
4,706
4,397
4,155
3,960
3,800
3,666
3,553
3,455
3,371
3,297
3,231
3,173
3,121
3,074
3,032
2,993
2,958
2,926
2,896
2,868
2,843
2,665
2,496
2,336
2,185
6157,285
99,433
26,872
14,198
9,722
7,559
6,314
5,515
4,962
4,558
4,251
4,010
3,815
3,656
3,522
3,409
3,312
3,227
3,153
3,088
3,030
2,978
2,931
2,889
2,850
2,815
2,783
2,753
2,726
2,700
2,522
2,352
2,192
2,039
xxi
Т а б л. 11. (Продолжение)
n
m
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
20
24
30
40
60
120
6208,730
99,449
26,690
14,020
9,553
7,396
6,155
5,359
4,808
4,405
4,099
3,858
3,665
3,505
3,372
3,259
3,162
3,077
3,003
2,938
2,880
2,827
2,781
2,738
2,699
2,664
2,632
2,602
2,574
2,549
2,369
2,198
2,035
1,878
6234,631
99,458
26,598
13,929
9,466
7,313
6,074
5,279
4,729
4,327
4,021
3,780
3,587
3,427
3,294
3,181
3,084
2,999
2,925
2,859
2,801
2,749
2,702
2,659
2,620
2,585
2,552
2,522
2,495
2,469
2,288
2,115
1,950
1,791
6260,649
99,466
26,505
13,838
9,379
7,229
5,992
5,198
4,649
4,247
3,941
3,701
3,507
3,348
3,214
3,101
3,003
2,919
2,844
2,778
2,720
2,667
2,620
2,577
2,538
2,503
2,470
2,440
2,412
2,386
2,203
2,028
1,860
1,696
6286,782
99,474
26,411
13,745
9,291
7,143
5,908
5,116
4,567
4,165
3,860
3,619
3,425
3,266
3,132
3,018
2,920
2,835
2,761
2,695
2,636
2,583
2,535
2,492
2,453
2,417
2,384
2,354
2,325
2,299
2,114
1,936
1,763
1,592
6313,030
99,482
26,316
13,652
9,202
7,057
5,824
5,032
4,483
4,082
3,776
3,535
3,341
3,181
3,047
2,933
2,835
2,749
2,674
2,608
2,548
2,495
2,447
2,403
2,364
2,327
2,294
2,263
2,234
2,208
2,019
1,836
1,656
1,473
6339,391
99,491
26,221
13,558
9,112
6,969
5,737
4,946
4,398
3,996
3,690
3,449
3,255
3,094
2,959
2,845
2,746
2,660
2,584
2,517
2,457
2,403
2,354
2,310
2,270
2,233
2,198
2,167
2,138
2,111
1,917
1,726
1,533
1,325
xxii
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
40
60
120
∞
5314
4135
1094
6213
7919
5050
8954
8382
1479
2311
4776
6570
8382
0115
5803
7005
7586
1094
3433
0610
6562
0690
7128
9162
8216
3361
1039
9481
5725
3652
6836
9154
7158
3072
3290
7042
7147
4386
5072
3676
7463
0120
6396
3901
8851
6387
9430
4474
6542
5889
0101
7397
2036
2267
8562
4161
7403
9362
5682
6679
8203
3993
6787
7480
4184
3374
6838
8315
2141
8865
8861
3584
5270
6512
2558
9279
5033
6122
4829
5190
1643
3136
3147
6319
0471
4963
4188
1752
7449
2378
2786
2139
7441
5673
5986
4049
8549
0193
4052
3647
6365,864
99,499
26,125
13,463
9,020
6,880
5,650
4,859
4,311
3,909
3,602
3,361
3,165
3,004
2,868
2,753
2,653
2,566
2,489
2,421
2,360
2,305
2,256
2,211
2,169
2,131
2,097
2,064
2,034
2,006
1,805
1,601
1,381
1,000
4101
6253
9629
4513
2226
0836
5307
8764
5489
3687
3741
2196
9953
4728
1907
0833
9202
9629
9709
4754
5825
3821
2625
2645
9664
1255
2383
8546
1653
2198
5132
1019
4387
2943
1904
1693
6005
1987
4201
6493
∞
6079
9711
5940
9121
0399
1992
4237
1197
5759
5643
9632
6883
6484
7880
7803
1932
2154
5940
5860
7818
n
3406
1413
6700
5477
5889
2099
5501
4215
6145
7198
0448
8247
8036
9019
4955
1790
5412
6700
9405
6700
m
0,5916
3127
3617
6635
9313
9470
5303
9031
8922
4398
9612
4601
2212
9192
2380
4448
5978
3617
2210
1374
Т а б л. 11.
(Окончание).
Т а б л. 12. Равномерно распределенные на [0,1]
случайные числа.
xxiii
Литература
УЧЕБНИКИ.
1. Н.Ш. Кремер. Теория вероятностей и математическая статистика. Учебник. М.:
Юнити, 2003.
2. В.П. Яковлев. Теория вероятностей и математическая статистика. М. «Дашков и
Ko», 2008.
3. В.А. Фигурин, В.В. Оболонкин. Теория вероятностей и математическая статистика.
Минск: ООО «Новое знание», 2000.
4. П.П. Бочаров, А.В. Печинкин. Теория вероятностей и математическая статистика.
М.: Физматлит, 2005.
5.И.А. Палий. Введение в теорию вероятностей. М.: Высшая школа, 2005.
6.В.Н. Калинина, В.Ф.Панкин. Математическая статистика. М.: «Дрофа», 2002.
7.А.Н. Бородин. Элементарный курс теории вероятностей и математической статистики. Санкт-Петербург: Лань, 2002.
8.В.Е. Гмурман. Теория вероятностей и математическая статистика. М.: Высшее образование, 2006.
9. Н.С. Аркашев, В.М. Бородихин, А.П. Ковалевский. Высшая математика. Том 4.2.
Теория вероятностей и математическая статистика. Новосибирск: Изд-во НГТУ, 2008,
с. 228.
ЗАДАЧНИКИ.
1. В.А. Ватутин, Г.И.Ивченко, Ю.И.Медведев, В.П. Чистяков. Теория вероятностей и
математическая статистика в задачах. М.: АГАР, 2003.
2. В.Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшее образование. 2007.
3. Е.И. Гурский. Сборник задач по теории вероятностей и математической статистике. Минск: Вышэйшая школа. 1975.
4. Сборник задач по высшей математике. Под ред. Ермакова.
5. И.В. Белько, Г.П. Свирид. Теория вероятностей и математическая статистика. Примеры и задачи. Минск: ООО «Новое знание», 2004.
6. К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко (под ред. С.Н.Федина).
Сборник задач по высшей математике. Т.2. М.: АЙРИС ПРЕСС, 2004.
7. Сборник задач по специальным главам математики. (Теория вероятностей. Математическая статистика). Составитель Крымских Д.А. Новосибирск: Изд-во НГТУ,
2005.
xxiv
Для
заметок
xxv
Михаил Юлианович Васильчик
Артем Павлович Ковалевский
Илья Михайлович Пупышев
Татьяна Вильевна Тренева
Владислав Владимирович Хаблов
Григорий Самуилович Шефель
МАТЕМАТИЧЕСКАЯ СТАТИСТИКА.
ПРИМЕРЫ И ЗАДАЧИ
Учебное пособие
В авторской редакции
Подписано в печать 29.06.11. Формат 60 х 84 1/16. Бумага офсетная. Тираж 300 экз.
Уч.-изд. л. 4 , 88. Печ. л. 5, 25. Изд. № 210. Заказ №
. Цена договорная.
Отпечатано в типографии
Новосибирского государственного технического университета
630092, г. Новосибирск, пр. К. Маркса, 20