оригинальный файл 94.7 Кб

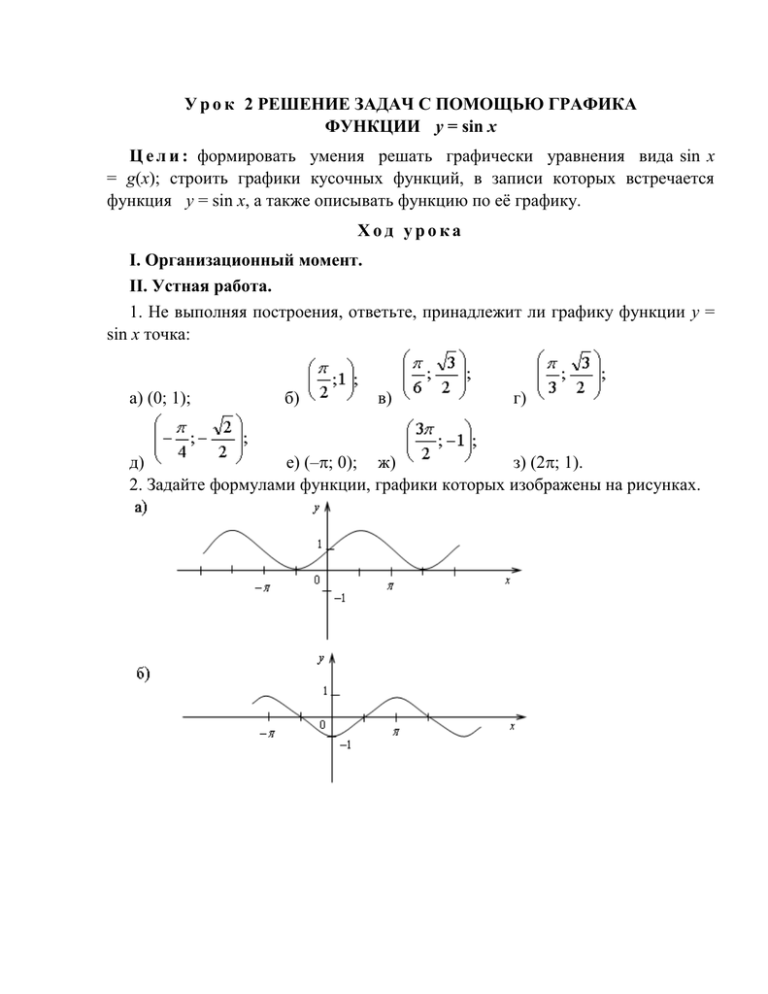
У р о к 2 РЕШЕНИЕ ЗАДАЧ С ПОМОЩЬЮ ГРАФИКА
ФУНКЦИИ у = sin х
Ц е л и : формировать умения решать графически уравнения вида sin x
= g(x); строить графики кусочных функций, в записи которых встречается
функция у = sin х, а также описывать функцию по её графику.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Не выполняя построения, ответьте, принадлежит ли графику функции у =
sin х точка:
а) (0; 1);
б)
в)
г)
д)
е) (–; 0); ж)
з) (2; 1).
2. Задайте формулами функции, графики которых изображены на рисунках.
III. Формирование умений и навыков.
Упражнения, выполняемые на этом уроке, можно разбить на группы.
1-я г р у п п а . Графическое решение уравнений.
2-я г р у п п а . Использование функциональной символики.
3-я г р у п п а . Кусочные функции и чтение графика функции.
1-я г р у п п а .
№ 10.11 (а; б), № 10.12 (а), № 10.13 (а).
Графический метод решения уравнений приводит учащихся к ситуации, когда
график функции строится не ради графика, а для решения другой задачи –
решения уравнения. Иными словами, построение графика является не целью, а
средством, помогающим решить уравнение. Это способствует и
непосредственному изучению функции, и ликвидации неприязненного
отношения учащихся к графикам и функциям.
Решение:
№ 10.11 (а).
Построим графики функций у = sin х (синусоида) и у = х +  (прямая,
проходящая через точки (0; ) и (–; 0)).
Построенные графики пересекаются в одной точке (–; 0). Проверим
полученный корень:
О т в е т : х = –.
№ 10.13 (а).
0 = 0 – верно, значит, – – корень.
ОДЗ: х –  0
х  

Графиком функции
сдвинутый на  вправо.
является
график
функции
Построенные графики пересекаются в одной точке (; 0). Проверим
полученный корень:
0 – 0 = 0; 0 = 0 – верно, значит,  – корень.
О т в е т : .
2-я г р у п п а .
№ 10.14 (а; б), № 10.15.
Учащиеся часто не могут исследовать функцию на четность и нечетность, так
как не знают определение и не понимают смысла записи f(–х). Данные
упражнения направлены
символики.
Решение:
№ 10.14.
на
осознанное
употребление
функциональной
значит, у = f(х) –
нечетная.
значит, у =
f(х) – нечетная.
№ 10.15.
3-я г р у п п а
№ 10.16 (а), № 10.17, № 10.18.
Для правильного формирования у школьников самого понятия функции у =
sin х необходимо рассмотреть кусочные функции.
Решение:
№ 10.16 (а).
№ 10.17.
б) (См. график функции).
в) 1)
2) Общего вида.
3) На
– убывает, на
4) Ограничена снизу.
5) унаим = –1, унаиб – не существует.
6) Непрерывна на D(f).
7)
8) На
№ 10.18.
– возрастает.
.
– выпукла вниз; на
– выпукла вверх.
б) (См. график функции).
в) 1)
2) Общего вида.
3) На
– убывает; на
4) Ограничена сверху.
5) унаиб = 1, унаим – не существует.
6) Имеет разрыв в точке х = 0.
– возрастает.
7)
8) На (–; 0) и на [0; ] выпукла вверх.
IV. Итоги урока.
Вопросы учащимся:
– Назовите D(f) и E(f) функции у = sin х.
– Назовите этапы решения уравнения графическим методом.
– Какая функция называется кусочной?
Домашнее задание: № 10.11 (в; г), № 10.12 (б), № 10.13 (б), № 10.14 (в; г), №
10.16 (б).