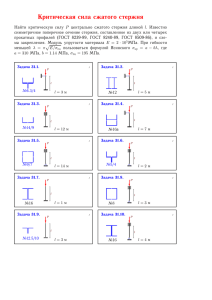
Задача 2.1. Жесткий стержень длиной l=1 м и массой M=1 кг

Задача 2.1.
Жесткий стержень длиной l=1 м и массой M=1 кг свободно висит на
горизонтальной идеально гладкой оси вращения О, как показано на рис. 1.
Рисунок 1
Ось вращения перпендикулярна плоскости рисунка. Малый шарик массой m=0,1кг,

летящий горизонтально со скоростью V0 , движется в плоскости рисунка и ударяет в
стержень. При этом взаимодействие шарика со стержнем может происходить в виде:
a) абсолютно упругого удара (АУУ);
b) неупругого удара (НУУ);
c) абсолютно неупругого удара (АНУУ).
Сразу после удара стержень вращается с угловой скоростью 0, а шарик

приобретает скорость VK и продолжает двигаться в плоскости рисунка. Другие
обозначения:
E - потеря энергии при ударе;

V0 M - минимальная начальная скорость шарика, при которой стержень после удара
совершает полный оборот;
K - угловая скорость стержня при прохождении им крайней верхней точки;
m - максимальный угол отклонения стержня от положения равновесия.
Другие исходные данные и искомые величины для каждого варианта задания
представлены в таблице:
№ Вар
2
Задано
V0
2V0m
VK
-
Виды
Определить
взаимодействия
АУУ НУУ АНУУ K m V0m E
+
+
+
+
Расчет следует начинать с определения характерной скорости шарика V 0 m
Решение:
Определим момент инерции стержня относительно оси O, проходящей так, как показано
на рисунке 1. Момент инерции стержня относительно оси, перпендикулярной ему и
проходящей через центр масс стержня, равняется:
IC 
ml 2
12
(1)
По теореме Штерна определим момент инерции стержня относительно оси O на рисунке
1. Расстояние от оси, проходящей через центр масс стержня, до оси O равняется
l l l
a    , поэтому момент инерции относительно оси O равняется:
2 6 3
I  I C  Ma 2 
Ml 2 Ml 2 7 Ml 2


12
9
36
(2)
2l
, после абсолютно
3
 2l  2l
неупругого соударения момент импульса системы: L  I 0  m  0  . Так как момент
33

импульса системы сохраняется, то имеем:
До соударения момент импульса системы равнялся L0  mV0
L0  L
(3)
2mV0l
4m0l 2
 I 0 
3
9
(4)
Подставим в выражение (4) значение момента импульса стержня (2) и получим:
2mV0l 7 M 0l 2 4m0l 2


3
36
9
(5)
2mV0l (7 M  16m)0l 2

3
36
Откуда:
0 
24mV0
(7 M  16m)l
Выберем нулевой уровень потенциальной энергии проходящим через центр масс
свободно висящего стержня, так как показано на рисунке 2:
(6)
Рисунок 2
В этом случае сразу после соударения потенциальная энергия стержня равняется нулю, то
есть E p  0 . Кинетическая энергия стержня сразу после соударения равняется:
Eк 
I 02
2
(7)
Учитывая, что момент инерции стержня определяется выражением (2), а его угловая
скорость сразу после соударения определяется выражением (6), получим:
2
56Mm2V02
1 7 Ml 2  24mV0 
Eк  

 
2 36  (7 M  16m)l  (7 M  16m) 2
(8)
В верхнем положении потенциальная энергия стержня равняется E pк  Mgh . Из рисунка 2
видно, что h 
E pк 
2l
, таким образом, получим:
3
2 Mgl
3
(9)
Кинетическая энергия в верхнем положении равняется:
Eкк 
I к2 7 Ml 2к2

2
72
По закону сохранения полной механической энергии для стержня получим:
(10)
E p  Eк  E pк  Eкк
(11)
Учитывая (8), (9), (10), получим:
56Mm2V02
2Mgl 7 Ml 2к2


(7 M  16m)2
3
72
(12)
Минимальную начальную скорость шарика V0m , при которой стержень совершает полный
оборот, найдём из условия, что в верхнем положении кинетическая энергия стержня
равняется нулю Eкк  0 . В этом случае выражение (12) имеет вид:
2
56Mm2V0m
2Mgl

2
(7 M  16m)
3
(13)
Отсюда V0m равняется:
V0 m 
Mgl (7 M  16m)2 7 M  16m gl

3  28Mm2
2m
21
(14)
По условию задачи V0  2V0 m , поэтому начальная скорость шарика равняется:
V0  2V0 m 
7 M  16m gl
m
21
(15)
Подставим в выражение (12) и получим:
2
56Mm2  7 M  16m gl 
2Mgl 7 Ml 2к2




(7 M  16m) 2 
m
21 
3
72
(16)
56Mgl 2Mgl 7 Ml 2к2


21
3
72
к 
144 g
g
 12
7l
7l
(17)
Найдём потерю энергии E при ударе. При соударении потенциальная энергия системы
не изменяется. Кинетическая энергия системы до соударения равняется кинетической
энергии шарика:
2
mV02 m  7 M  16m gl  m (7 M  16m) 2 gl (7 M  16m) 2 gl
Eк1 
  

  
2
2 
m
21 
2
m2
21
42m
(18)
Угловая скорость стержня сразу после соударения определяется выражением (6) и в
нашем случае равняется:
0 
24mV0
24m
7 M  16m gl
g


 24
(7 M  16m)l (7 M  16m)l
m
21
21l
(19)
Сразу после соударения стержень и шарик движутся вместе, поэтому кинетическая
энергия системы равняется:
I 2 m 
2l  7 Ml 2 192 g 2ml 2 192 g
Eк 2  0   0   


2
2
3
72 7l
9
7l
(7 M  16m) 192 gl 1

 (7 M  16m) gl
72
7
3
2
(20)
Из закона сохранения энергии следует, что потеря энергии при ударе равняется:
(7 M  16m) 2 gl 1
 (7 M  16m) gl 
42m
3
 7 M  16m 1  Mgl (7 M  16m)
 gl (7 M  16m) 
 
3
6m
 42m
E  Eк1  Eк 2 
(21)
Таким образом, мы получили:
V0 m 
7M  16m gl
2m
21
к  12
E 
g
7l
Mgl (7 M  16m)
6m
Подставляя числовые значения, получим:
V0 m 
7  16  0.1 9.8 1
 29.4 м / с
2  0.1
21
к  12
E 
9.8
 14.2 рад / с
7 1
1 9.8 1 (7  16  0.1)
 140.5 Дж
6  0.1
Ответ:
V0 m 
7M  16m gl
,
2m
21
к  12
g
,
7l
E 
Mgl (7 M  16m)
6m
V0 m  29.4 м / с , к  14.2 рад / с , E  140.5 Дж .