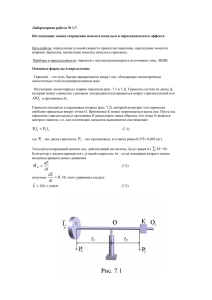
Момент инерции, вращающий момент, момент ... нутация. Соберите гироскоп как показано на Рис. 1. Прикрепите на оси

Темы для изучения
Момент инерции, вращающий момент, момент импульса,
нутация.
Принцип
При незначительном смещении оси вращения свободного
гироскопа наблюдается нутация. Исследуется зависимость
между частотой нутации и частотой гироскопа для различных
моментов инерции.
К гироскопу в карданном подвесе для прецессии прикреплены
дополнительные гири.
Оборудование
Гироскоп Магнуса с пособием
Секундомер, цифровой, 1/100 с
Стробоскоп с цифровым индикатором
Цель
1.
2.
02550.00 1
03071.01 1
21809.93 1
Определить зависимость частоты прецессии от
вращающего момента и угловой скорости гироскопа.
Определить зависимость частоты нутации от угловой
скорости и момента инерции.
Замечание
Прилагается учебное пособие (128 стр.) с дополнительными
описаниями экспериментов.
Рис. 1: Гироскоп в карданной оправе.
Установка и ход работы
Соберите гироскоп как показано на Рис. 1. Прикрепите на оси
или диске (роторе) дополнительные гири. Диск должен
находиться в положении безразличного равновесия во всех
пространственных направлениях и оставаться неподвижным.
Для этого отрегулируйте его при помощи двух скользящих
гирек. Для определения частоты прецессии расположите
дополнительные гири на оси гироскопа и слегка завинтите их.
При помощи двух дополнительных гирь можно получить три
комбинации ( m1 ,0 ), ( m2 , m1 ) и ( m2 ,0 ).
При помощи пусковой рукоятки приведите гироскоп в
движение. Измерьте угловую скорость стробоскопом, а частоту
прецессии – секундомером. Рекомендуется измерить двойную
частоту стробоскопом и половину периода прецессии
секундомером.
Снимите дополнительные гири. Приведите гироскоп в
движение. Рукой слегка коснитесь оправы, чтобы вызвать
нутацию.
Частота нутации измеряется стробоскопом. Определите
частоту нутации для различных скоростей гироскопа и при
различных
дополнительных
гирях
(расположенных
симметрично относительно друг друга).
Рис. 2: Подвижная система координат для гироскопа.
Теория и расчет
В инерциальной системе отсчета XYZ уравнение движения

твердого тела с моментом импульса L , к которому

прикладывается вращающий момент T , имеет вид

dL 
 T.
dt
Рис. 3: Зависимость частоты прецессии от частоты гироскопа с
различными дополнительными гирями.
Момент импульса гироскопа можно разложить на

составляющую по оси симметрии Ls , выходящей только из

 IxI y d /2

Iy
d / Tx

 x 
,


1
 ( I z  ) 2 dt 2

( I sz  z ) 2 dt
 s z

ротора, и остаток Lns :
 

L  LS  Lns .
При преобразовании уравнения движения для подвижной
системы координат xyz , которая вращается с угловой
скоростью  с началом в точке центра масс, а оси проходят
по внутренней рамке гироскопа и оси симметрии (см. Рис 2)
получаем:
  

d Ls d / 

Lns    Ls  Lns  T
dt
dt
/
 IxI y d /2

T

 1 y  z x .
 ( I z  ) 2 dt 2

I s z
 s z

( T y не учитывается для гирь, расположенных на оси ротора.)
Введя эйлеровы углы  и  , получим:
d /
dt
d/
 y  sin 

dt
Tx  mgr  sin  ,
x 
Возьмите производную по времени во вращающейся системе
(отмечено пунктиром). Если момент импульса ротора по оси
симметрии постоянный:


Ls  I s    I sz  z ,
где момент инерции I sz ротора лежит вдоль оси симметрии, а
 z - угловая скорость и соблюдается условие
LS  Lns ,
получаем основное уравнение для гироскопа:
d/
Lns    Ls  T .
dt
Из выражения (1) получаем независимые уравнения для
компонентов (1), характеризующие прецессию и нутацию:
(1)
где m - масса гири, которая расположена на расстоянии r от
центра и вызывает благодаря ускорению свободного падения
вращательный момент.
При начальных условиях
d 
dt
d 
dt
0,
t 0
 0
t 0
имеем:
d /

dt
I y mgr
I z
( z  0 ) sin  0  sin s z
I x I s z
IxIy
I z
d /
mgr
mgr
 z  (0  z ) cos s z t .
dt
I s z
I s z
IxI y
При начальном условии
0 
mgr
I sz  z
,
частота прецессии при постоянном  равна
 pr
d /
mgr 1
 z 
.
dt
I s z z
(2)
Используя функцию
Y  A X B ,
из графика на Рис. 3 и выражения (2), получаем показатели
B1  1,02  0,01,
B2  1,01  0,005 ,
Рис. 4: Зависимость частоты нутации от частоты гироскопа f z
B3  1,01  0,005 .
Если коснуться рукой оси симметрии гироскопа, то при
d /
 0,
dt
с различными дополнительными гирями ( I x , z I y ).
Если частота прецессии невелика по сравнению с частотой
ротора  z , то
Iy
( I sz  z ) 2
ось будет двигаться с частотой нутации
 nu 
mgr cos  1.
Этим условием можно пренебречь:
 IxI y d /2
 d /
 z


1
2
2
 ( I  ) dt
 dt  0
 s z

/
2
 IxIy d
 d / mgr
 z


1
 ( I  ) 2 dt 2
 dt  I z  .
s z
 s z

Iz
IxI y
z .
Используя функцию
Y  A B X ,
из графика на Рис. 4 и выражения (3), получаем компоненты
B1  0,95  0,02,
B2  0,82  0,02,
B3  0,57  0,02 .
(3)