Печатная основа.
реклама
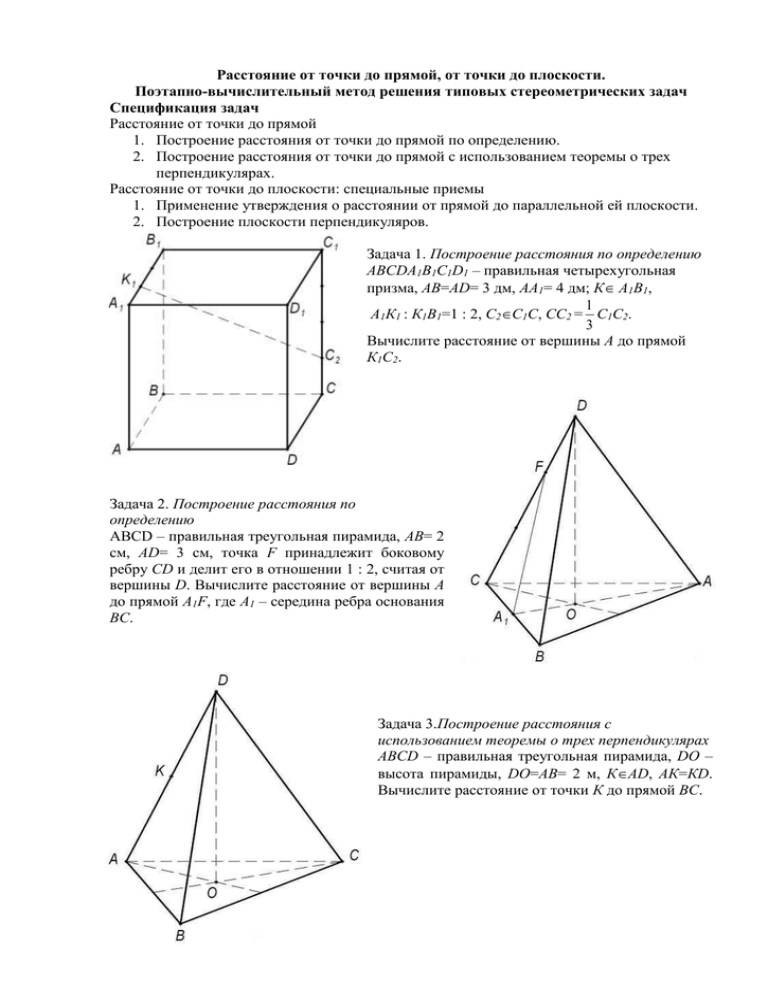
Расстояние от точки до прямой, от точки до плоскости. Поэтапно-вычислительный метод решения типовых стереометрических задач Спецификация задач Расстояние от точки до прямой 1. Построение расстояния от точки до прямой по определению. 2. Построение расстояния от точки до прямой с использованием теоремы о трех перпендикулярах. Расстояние от точки до плоскости: специальные приемы 1. Применение утверждения о расстоянии от прямой до параллельной ей плоскости. 2. Построение плоскости перпендикуляров. Задача 1. Построение расстояния по определению АВСDА1В1С1D1 – правильная четырехугольная призма, АВ=АD= 3 дм, АА1= 4 дм; К А1В1, 1 А1К1 : К1В1=1 : 2, С2С1С, СС2 = С1С2. 3 Вычислите расстояние от вершины А до прямой К1С2. Задача 2. Построение расстояния по определению АВСD – правильная треугольная пирамида, АВ= 2 см, АD= 3 см, точка F принадлежит боковому ребру СD и делит его в отношении 1 : 2, считая от вершины D. Вычислите расстояние от вершины А до прямой А1F, где А1 – середина ребра основания ВС. Задача 3.Построение расстояния с использованием теоремы о трех перпендикулярах АВСD – правильная треугольная пирамида, DО – высота пирамиды, DО=АВ= 2 м, КАD, АК=КD. Вычислите расстояние от точки К до прямой ВС. Задача 4. Построение расстояния с использованием теоремы о трех перпендикулярах АВСА1В1С1 – правильная треугольная призма, АВ = 3 см, АА1 = 2 см, К1В1С1, К1С1=2В1К1. Вычислите расстояние от вершины С до прямой А1К1. Задача 5. Построение расстояния с использованием теоремы о трех перпендикулярах АВСDР – правильная четырехугольная пирамида, АВ=АР= 3; QРD, РQ= 2QD, КАВ, ТАD, АК = DТ = 2. Вычислите расстояние от точки Q до прямой КТ. Задача 6. Два подхода к построению расстояния: использование утверждения о расстоянии от прямой до параллельной ей плоскости; использование плоскости перпендикуляров АВСD – правильная треугольная пирамида, АВ = 2м, АD = 3м, точка К – середина ребра основания АВ. Вычислите расстояние от точки К до боковой грани АСD. Задача 7. Использование плоскости перпендикуляров АВСDА1В1С1D1 – куб с ребром, равным 4 см, В2ВВ1, С2СС1, С1С2 : С2С=ВВ2 : В2В1=1 : 3. Вычислите расстояние от вершины В до плоскости, проходящей через точки А1, В2 и С2 . Задача 8. АВСDА1В1С1D1 – куб с ребром 4 см, точка D2 – середина бокового ребра DD1, точка С2 принадлежит боковому ребру СС1 и делит его в отношении 1 : 3, считая от вершины С. Вычислите расстояние между прямыми C2D1 и АD2. Задача 9. АВСDР – правильная четырехугольная пирамида, АВ=2 м, АР=3 м; Р1, Р2РD, РР1=Р1Р2=Р2D. Вычислите расстояние между прямыми АР2 и СР1.







