МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ «МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (национальный исследовательский университет)» МАИ

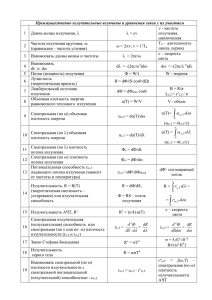
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ Государственное БЮДЖЕТНОЕ образовательное
учреждение
высшего профессионального образования
«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(национальный исследовательский университет)» МАИ
ФИЛИАЛ «ВЗЛЕТ»
Нестеров С.В.
Лабораторные работы
по курсу
«Оптико-электронные системы извлечения информации»
2015г.
Лабораторная работа № 1
Цель работы: Исследовать излучение абсолютно черного тела.
Введение
Можно заставить светиться любое тело, сообщая ему необходимую
энергию нагреванием. Для поддержания излучения неизменным, необходимо
убыль энергии, уносимую излучением, пополнять сообщением
соответствующего количества тепла.
Данный вид свечения наиболее распространен и называется тепловым
излучением. Оно имеет место и при низких температурах (отличных от
абсолютного нуля), но в этих условиях излучения практически
ограничивается очень длинными инфракрасными (ИК) волнами.
Энергия излучения. Энергетические величины.
Энергией излучения Qе называется энергия, переносимая излучением
оптических лучей. Энергия излучения измеряется в любых единицах, в
которых измеряют различные виды энергии, например, в джоулях.
Энергию излучения, переносимую в единицу времени, называют
потоком излучения Фе. Если за время t излучается энергия Qе, то поток
излучения равен
Фе = Qе / t
(1.1)
Поток измеряют в единицах мощности – ваттах (Вт).
Для источников излучения с непрерывным спектром суммарный поток
излучения определяется площадью, заключенной между спектральной
кривой излучения и осью абсцисс:
Фе = ∫ Фе,λ · d λ,
(1.2)
где Фе,λ - функция распределения энергии по длинам волн, зависящая
от природы излучающего тела и тех условий, при которых происходит
излучение.
Например, для частного случая излучения, характеризуемого
функцией, Фе,λ (рис.1) поток излучения в интервале длин волн от λ1 до λ2
равен площади заштрихованного участка. Полный поток, относящийся ко
всем длинам волн от λ1 = 0 до λ2 = ∞ равен
Фе = ∫ Фе,λ · d λ.
В зависимости от спектрального состава энергии излучения и
спектральной чувствительности приемника излучения энергию излучения
можно выразить в двух системах единиц: энергетической
и
светотехнической. Светотехническая система используется только в видимой
области спектра, т.к. она базируется главным образом на световых
ощущениях человеческого глаза. При описании функционирования оптикоэлектронных систем, особенно в ИК области, пользуются энергетической
системой единиц.
Сила излучения Ιе представляет собой отношение потока излучения Фе ,
излучаемого в данном направлении внутри телесного угла ω к величине
этого угла:
Ιе = Фе / ω
(1.3)
Выражение (1.3) справедливо только в случае точечного источника
излучения и равномерного распределения внутри телесного угла (рис.2)
Телесный угол ω равен отношению площади поверхности Sс, вырезанной на
сфере конусом с вершиной в центре сферы, к квадрату радиуса сферы r:
ω = Sс/ r 2
(1.4)
Телесный угол с вершиной в центре сферы, вырезающий на
поверхности сферы площадь, равную квадрату радиуса сферы, принят за
единицу измерения телесного угла и называется стерадианом (ср). Телесный
угол ω связан с плоским углом α соотношением
ω = 2π · (1- cos α)
(1.5)
Телесный угол, охватывающий все пространство вокруг точечного
источника излучения, равен 4π. Поэтому для источника, равномерно
излучающего во все стороны, сила излучения в любом направлении будет
равна
Ιе = Фе / 4π
Сила излучения измеряется в Вт/ср.
Энергетическая светимость (излучательность)
Ме - это поток излучаемый или отражаемый единицей поверхности во
всех направлениях
Ме = Фе / Sизл
(1.6)
Ранее для данной величины применялся термин «плотность
излучения», но от него отказались из-за его неопределенности, т.к. плотность
может быть поверхностной, объемной, угловой, спектральной, а излучение –
испускаемым, падающим.
Единица энергетической светимости – Вт/м2.
Энергетическая яркость
Энергетическая яркость Lе – это сила излучения с единицы
излучающей поверхности в заданном направлении.
Пусть малая площадка Sизл создает силу излучения в направлении,
составляющем угол α с нормалью к площадке (рис.3).
Если смотреть в этом направлении, то будет казаться, что площадка
имеет размер
S' = Sизл · cos α , где S' - проекция площадки Sизл на
плоскость перпендикулярную рассматриваемому направлению.
Энергетическая яркость поверхности Sизл
есть отношение силы
излучения Ιе к проекции излучающей площадки Sизл на плоскость,
перпендикулярную направлению излучения (S''):
Lе = Ιе / S' = Ιе / (Sизл ·cos α)
(1.7)
т.е. энергетическая яркость равна силе излучения, отнесенной к
единице видимой поверхности
источника излучения. Энергетическая
2
яркость измеряется в Вт/(ср·м ).
Облученность или энергетическая освещенность (рис.4) поверхности
равна отношению лучистого потока к площади
облучаемой поверхности, по которой он равномерно распределен:
Ее = Фе / Sобл
(1.8)
Для точечного источника, т.е. для источника, находящегося на
достаточном удалении, легко вывести зависимость между облученностью и
силой излучения. Пусть на площадку Sобл, расположенную на расстоянии ℓ
от источника излучения, падают под углом α лучи, заключенные внутри
телесного угла ω. Телесный угол из (4) ω = S' / ℓ2 , где
S' - площадка перпендикулярная направлению излучения: S' = Sобл · cos α,
т.е ω = Sобл · cos α / ℓ2, откуда Sобл = ωℓ2/ cos α, а облученность из (1.8)
Ее = Фе ·cos α / ωℓ2.
Из (1.3) Фе/ ω = Iе , таким образом
Ее = Iе·cos α /ℓ2
(1.9)
Выражение (1.9) характеризует «закон квадратов расстояний», по
которому облученность поверхности, создаваемая точечным источником
прямо пропорциональна силе излучения и косинусу угла падения лучистого
потока и обратно пропорциональна квадрату расстояния между источником и
облучаемой поверхностью.
Облученность измеряется в Вт/м2.
Энергетическая экспозиция Не - характеризует облученность единицы
площади поверхности за определенное время
Не = Ее· t
(1.10)
2
2
Лучистую экспозицию измеряют в Вт·с/м или Дж/м .
Закон Ламберта
Если энергетическая яркость Lе поверхности источника излучения во
всех направлениях одинакова и не зависит от направления излучения, то в
этом случае выполняется закон Ламберта , или закон косинуса, по которому
сила излучения поверхности пропорциональна косинусу угла излучения т.е.
Iеα = Iео ·cos α
(1.11)
где Iео – сила излучения в направлении, перпендикулярном поверхности ;
α - угол между рассматриваемым направлением и перпендикуляром к
поверхности.
Кривая
распределения силы излучения представляет собой
окружность, касающуюся излучающей поверхности.
Закон Ламберта строго выполняется только для абсолютно черного
тела (АЧТ) и идеально рассеивающих или идеально поглощающих (матовых)
поверхностей. Для поверхностей, подчиняющихся
закону Ламберта,
энергетическая светимость поверхности из (1.3), (1.6), (1.7) и (1.11) равна ее
энергетической яркости , умноженной на π:
Ме = π · Lе
(1.12)
Абсолютно черное тело
При падении потока излучения на тело, часть его может пройти через
тело, часть - отразится, а оставшаяся часть поглощается, переходя в тепло,
вызывающее увеличение температуры тела. Поглощательная способность
тела характеризуется спектральным коэффициентом поглощения αλ ,
который является относительной величиной, показывающей какая часть
падающей на поверхность тела лучистой энергии с определенной длиной
волны λ поглощается при температуре Т:
αλ = Фе,λпогл / Фе,λ
(1.13)
Если какое-либо тело полностью поглощающее на него излучение любой
длины волны, т.е. если у этого тела αλ = 1, то его называют АЧТ или черным.
В природе не существует тел, имеющих свойства абсолютно черного
тела для всех длин волн. Даже такие черные на вид поверхности, как
покрытые слоем сажи или платиновой черни, имеют поглощательную
поверхность αλ , близкую к единице лишь в ограниченном спектральном
диапазоне; в длинноволновой ИК области спектра их поглощательная
способность становится значительно меньше единицы.
Можно искусственно создать модель АЧТ (рис.6) с очень высокой
степенью приближения. Такой моделью может быть замкнутая нагреваемая
полость с непрозрачными стенками, внутренняя поверхность которой
обладает хорошей поглощательной способностью.
В полости проделывают отверстие, очень малое по сравнению с ее
размерами. Поток излучения, попавший через отверстие внутрь полости,
испытывает большое число отражений, теряя при каждом отражении
большую часть энергии, и почти полностью поглощается, т.к. выйти из
полости через малое отверстие может только ничтожная его часть. При
нагреве полости ее отверстие будет являться «черным» излучателем, т.е.
вести себя как АЧТ, имеющее площадь, равную площади отверстия.
Степень совершенства модели, т.е. приближения к АЧТ,
характеризуется эффективным коэффициентом теплового излучения εэф,
представляющим собой отношение потока энергии излучения, исходящего из
отверстия модели Фе к потоку энергии излучения АЧТ при той же
температуре
εэф = Фе / Фео
(1.14)
Из (1.14) следует, что εэф < 1. εэф зависит от формы полости и размера
излучающего отверстия, материала внутренних стенок полости и неравномерности температуры внутренних стенок. Для полости любой формы
εэф = ε [1+ (1- ε) · (S1/ Sпол –S1/S0)]
ε (1 - S1/ Sпол) + S1/ Sпол
(1.15)
________где ε – коэффициент теплового излучения материала стенок полости;
S1 - площадь отверстия;
Sпол – полная площадь поверхности полости, включая площадь
отверстия;
S0 – площадь поверхности сферы, диаметр которой равен глубине
полости (расстоянию между плоскостью отверстия и самой дальней точкой
полости).
Для сферической полости (1.15) имеет более простой вид
ε
εэф =
ε (1 - S1/S) + S1/ Sпол
(1.16)
На практике вместо (1.16) части пользуются приближенной формулой
εэф ≈ 1-ρ· S1/ Sпол
(1.17)
где ρ – коэффициент отражения материала полости.
Закон Кирхгофа
Закон Кирхгофа устанавливает связь между излучательной и
поглощательной способностью тел: «Отношение спектральной плотности
энергетической светимости любого тела Ме,λ к спектральному коэффициенту
поглощения этого тела αλ для определенных длин волн, температуры и
направления излучения есть величина постоянная для всех тел, независимо
от их природы
Ме,λ1 / αλ1 = Ме,λ2 / αλ2 = ... = Мео,λ / αоλ = сonst
(1.18)
о
где Ме ,λ - спектральная плотность энергетической светимости АЧТ;
αоλ – спектральный коэффициент поглощения АЧТ».
Т.к. αоλ = 1, то (1.18) имеет вид:
Ме,λ1 / αλ1 = Мео,λ = ƒ(λ, Т)
(1.19)
(1.19) связывает излучение реальных тел с излучением АЧТ и
поглощательной способностью тела, чем больше тело поглощает энергии,
тем больше оно излучает. Т.к. у АЧТ поглощательная способность является
наибольшей (αоλ = 1), то оно при данной температуре излучает максимальное
количество энергии.
Закон Стефана-Больцмана
Закон Стефана-Больцмана формируется следующим образом:
энергетическая светимость АЧТ пропорциональна четвертой степени его
абсолютной температуры:
Мео = σ·Т4
(1.20)
где σ = 5,67· 10-8 Вт/(м2·к4) - постоянная излучения.
Из (1.20) видно, что увеличение температуры тела проводит к резкому
возрастанию излучения АЧТ. При 4000К мощность излучения с 1 см2
превышает 1кВт.
Для АЧТ с площадью S поток энергии излучения равен:
Фе = Мео· Sизл = σ·Sизл·T4
(1.21)
Из (1.21) находят поток излучения АЧТ в пределах полусферы.
Согласно (1.12) яркость излучения
Lео = Мео / π = σ·T4/ π
(1.22)
Из (1.9) облученность площадки, находящейся на расстоянии ℓ от АЧТ
Ее = Iе ·cos α /ℓ2 = Lео · Sизл · cos α /ℓ2 = σ·T4· Sизл · cos α / π ℓ2 (1.23)
При температурах АЧТ (или другого объекта), соизмеримых с
температурой окружающей среды (То) в (1.20), (1.21), (1.22) и (1.23)
необходимо ввести температурную поправку (при этом предполагается, что
среда обладает свойством АЧТ). Тогда (1.23) имеет вид:
Еео = [(Фе, объект – Фе, фон) / π ℓ2] ·cos α
(1.24)
Закон Вина
Вин установил, что излучение достигает максимума при определенной
длине волны λ, причем каждому значению температуры Т АЧТ
соответствует длина волны λmax . Длина волны λmax, соответствующая
максимуму спектральной плотности энергетической светимости АЧТ,
обратно пропорциональна температуре тела
λmax = С/Т
(1.25)
-2
где С – константа, С = 0,2898 ·10 м ·К, если λmax выражена в м и
С = 2898 мкм·К, если λmax выражена в мкм.
Таким образом, чем выше температура тела, тем на более короткую
волну приходится максимум распределения спектральной плотности
излучения.
При практически достижимых температурах длина волны , на которую
приходится максимум излучения АЧТ, находится в ИК области спектра.
Только при Т = 4000К максимум совпадает с красной, а при температуре
5000К- с желтой областью видимого спектра.
Вином было выведено еще одно важное соотношение,
устанавливающее величину спектральной плотности энергетической
светимости АЧТ в точке, соответствующей λmax , которое называют вторым
законом Вина:
Мео λmax = С '·T5
(1.26)
-5
3
5
где С' = 1,3·10 Вт/м ·К ).
Максимальная спектральная плотность энергетической светимости
АЧТ возрастает пропорционально пятой степени абсолютной температуры.
Экспериментальная часть
Описание экспериментальной установки
В ходе эксперимента исследуется излучение модели АЧТ. Внутренняя
полость представляет собой цилиндр глубиной 20 см и диаметром 8 см.
Выходное отверстие регулируется по диаметру за счет смены калибровочных
диафрагм от 0,3 до 10 мм. Температура внутренней полости может достигать
величины 2000 К. Коэффициент поглощения внутренних стенок полости
составляет 0,9.
АЧТ размещается на поворотном стенде, позволяющем определить
направление с точностью до 1.
Излучение АЧТ измеряется с помощью радиометра, на входе которого
размещается объектив диаметром 10 см (рис.7).
Показания радиометра снимаются с индикатора, проградуированного в
единицах освещенности (Вт/м2) . Расстояние от выходного отверстия АЧТ до
объектива радиометра выдерживается равным 2 м. Перед началом излучения
АЧТ включением модели на индикаторе радиометра устанавливается нулевое
значение.
Порядок выполнения лабораторной работы
1. Замерить температуру воздуха в месте расположения установки.
2. Для различных диафрагм модели АЧТ (не менее 3) по выражению
(1.17) рассчитать коэффициент модели АЧТ. При данных диафрагмах при
произвольных температурах модели АЧТ произвести замеры освещенности
радиометра. Завести данные в табл.1.1, рассчитать необходимые данные в
табл.1.1.
3. Для различных диафрагм модели АЧТ 0,3 ; 5; 10 мм и температуре
модели 2000 К, поворачивая стенд (шаг установить самостоятельно),
произвести замеры освещенности радиометра. Экспериментальные и
расчетные данные занести в табл.1.2 для каждого значения диафрагмы.
Таблица 1.1
Определение эффективного коэффициента модели АЧТ
Величина
диафрагмы, мм
Температура АЧТ,К
Наружная
температура, К
Поток излучения
АЧТ в данных
условиях, Вт
Поток излучения
фона, Вт
Поток излучения
модели АЧТ, Вт
Освещенность
радиометра, Вт/м2
Коэффициент
модели АЧТ по
данным
эксперимента
Коэффициент
модели АЧТ по
выражению (17)
Таблица 1.2
Диафрагма модели
АЧТ
d АЧТ =
Исследование закона Ламберта на модели АЧТ
Угол поворота, град
Сила излучения АЧТ по
выражению (11), Вт/м2
Сила излучения модели
АЧТ, Вт/м2
Освещенность
радиометра, Вт/м2
Погрешность выполнения закона Ламберта, %
4.Для одной самостоятельно выбранной диафрагмы модели АЧТ
произвести замеры освещенности радиометра при различных значениях
температуры модели (не менее 10 значений). Экспериментальные и
расчетные данные занести в табл.1.3.
Таблица 1.3
Исследование закона Больцмана на модели АЧТ
Температура АЧТ, К
Освещенность радиометра АЧТ,
Вт/м2
Светимость
По вырамодели АЧТ, Вт/ср жению (1.23)
По выражению (1.24)
Светимость АЧТ, Вт/ср
Коэффициент излучения модели
АЧТ
Построить графики зависимости сил излучения модели АЧТ,
рассчитанных по экспериментальным данным с помощью выражений (1.23) и
(1.24).
Контрольные вопросы:
1. Какие особенности имеет излучение у поверхностей, подчиняющихся закону Ламберта ?
2. Что такое черное тело ? Что такое нечерное тело ? Какое излучение
называется селективным, а какое серым ?
3. Во сколько раз возрастет интегральная энергетическая светимость
черного тела, если его температуру увеличить в два раза ?
4. На какую длину волны приходится максимум излучения АЧТ,
нагретого до температуры 600 К ?
5. Какую погрешность вносит неучет температуры фона?
Лабораторная работа № 2
Цель работы: Исследовать спектральное распределение излучения АЧТ.
Закон Планка
Планку удалось найти общее уравнение распределения энергии по
спектру АЧТ, точно совпадающее с опытными данными. Для этого Планку
пришлось отойти от классических представлений о природе излучения и
выдвинуть предположение о том, что излучение испускается не непрерывно,
а в виде отдельных порций энергии – квантов εф = h·ƒ. Была получена
формула Ме,λ = ƒ (λ,t) = 2π ∙ħ∙c2∙λ-5 (есħ/kт λ – 1)-1
(2.1)
где с – скорость распространения излучения в вакууме,
k = 1,3805∙10-23 Дж/К – постоянная Больцмана,
ħ = 6,626∙10-34 Дж∙с – постоянная Планка.
Обозначив 2π kc2 = С1 и ħ∙c/k = С2, (2.1) запишется как
Мео λmax = С1 λ-5(ес2/т λ – 1)-1
(2.2)
-18
2
-2
где С1 = 3,74 ∙10 Вт∙м , С2 = 1,44 ∙10 м, К =14400 мкм∙К.
Следует иметь в виду, что при С2 / λТ >>1 можно использовать более
простую формулу Вина:
Мео,λ = С1∙λ-5 е -с2/т λ
(2.3)
Формула (2.3) дает погрешность по сравнению с (2.2) не более 10 %
при λТ < 6000 мкм∙К и не более 1% при λТ < 3000 мкм∙К.
При С2/ λ Т<<1 можно использовать формулу Рэлея-Джинса
Мео,λ = С1/С2 ∙ λ-4 Т
(2.4)
Погрешность расчетов по (2.4) составляет не более 10% при
λ Т >700 000 мкм∙К и 1% при λ Т >1 400 000 мкм∙К.
Проинтегрировав (2.2) по всему диапазону длин волн, получим
энергетическую светимость АЧТ согласно (1.20) , а продифференцировав
(2.2) для определения максимума излучения, получим длину волны согласно
(1.25).
Описание экспериментальной установки.
В эксперименте используются модель АЧТ с диаметром отверстия,
равным 3 мм, описанная выше, монохроматор и фотометр с регистрирующим
устройством. Вместо монохроматора может использоваться набор
узкополосных ИК – фильтров.
Размещение аппаратуры аналогично схеме (рис.7), только модель АЧТ
в процессе работы не поворачивается, а вместо радиометра используется
фотометр с монохроматором. Регистрирующее устройство в качестве
выходного параметра имеет величину падающего потока (Вт). Диаметр
входного отверстия фотометра – 5см.
Порядок выполнения лабораторной работы
1. Для заданного ряда температур АЧТ снять характеристики
спектральной светимости АЧТ.
Данные эксперимента занести в табл.2.1.
Таблица 2.1
Т=
Снятие характеристик спектральной светимости
Длина волны,
мкм
Падающий
поток, Вт
Светимость
модели АЧТ,
Вт/м2
Интервал шаг измерений по длине волны выбирать самостоятельно, но
менее 0,1 мкм (стараясь избегать чрезмерного увеличения объема данных, но
в то же время не пропустить характерные точки кривой).
2. По данным эксперимента п.1 построить графики спектральной
зависимости модели АЧТ при различных температурах.
3. По данным эксперимента п.1 построить график зависимости
максимальной величины спектральной светимости АЧТ (модели АЧТ) от
температуры.