А13_разбор
реклама

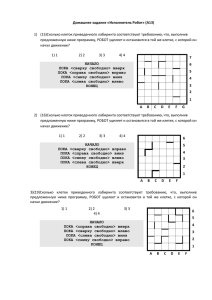
Давайте разберем одну из задач ЕГЭ предыдущих лет и попытаемся выявить некоторые правила! Текст задачи: Система команд исполнителя РОБОТ, «живущего» в прямоугольном лабиринте на клетчатой плоскости: вверх вниз влево вправо При выполнении любой из этих команд РОБОТ перемещается на одну клетку соответственно: вверх ↑, вниз ↓, влево ←, вправо →. Четыре команды проверяют истинность условия отсутствия стены у каждой стороны той клетки, где находится РОБОТ: сверху свободно снизу свободно слева свободно справа свободно Цикл ПОКА < условие > команда выполняется, пока условие истинно, иначе происходит переход на следующую строку. Если РОБОТ начнёт движение в сторону стены, то он разрушится и программа прервётся. Сколько клеток лабиринта соответствуют требованию, что, выполнив предложенную программу, РОБОТ уцелеет и остановится в той же клетке, с которой он начал движение? НАЧАЛО ПОКА < справа свободно > вниз ПОКА < снизу свободно > влево ПОКА < слева свободно > вверх ПОКА < сверху свободно > вправо КОНЕЦ 1) 1 2) 3 3) 5 4) 7 Решение: Сначала построим траекторию движения робота. Она изображена на рисунке: Черной точкой обозначена клетка, из которой начнет движение робот. Отсюда мы видим 1-ое правило: Нужно просмотреть программу с последнего условия! И выбрать только те клетки, которые ограничены этим условием! В нашем случае мы имеем: “Пока < сверху свободно > вправо”. Из рисунка видно, что клетка, из которой должен начать движение робот, должна быть сверху ограничена барьером. Из этого напрашивается 2-ое правило: Если клетка не имеет границ, то она не является кандидатом и ее не нужно рассматривать! Но если пустые клетки не рассматриваем, тогда что же нам делать с клеткой которая со всех сторон окружена барьерами? И вот, наконец, и 3-ье правило: Если клетка имеет барьер со всех четырех сторон, то мы смело можем говорить, что она удовлетворяет всем условием. А это означает то, что она нам подходит! Ну а дальше все просто. Отмечаем клетки, ограниченные сверху барьером. Это и будут потенциальные клетки, которые нам нужно найти. Теперь проверим каждую из этих точек. Для каждой точки нарисуем траекторию движения робота: Там, где стрелочка касается барьера или стены лабиринта, произошло разрушение робота. Только три клетки удовлетворяют требованиям задачи: робот не разрушится и вернется в ту же клетку, с которой начал движение. На рисунке они обозначены розовыми большими овалами. Ну, вот и всё. Правильный ответ 2!