Вариант решения задания №4
реклама
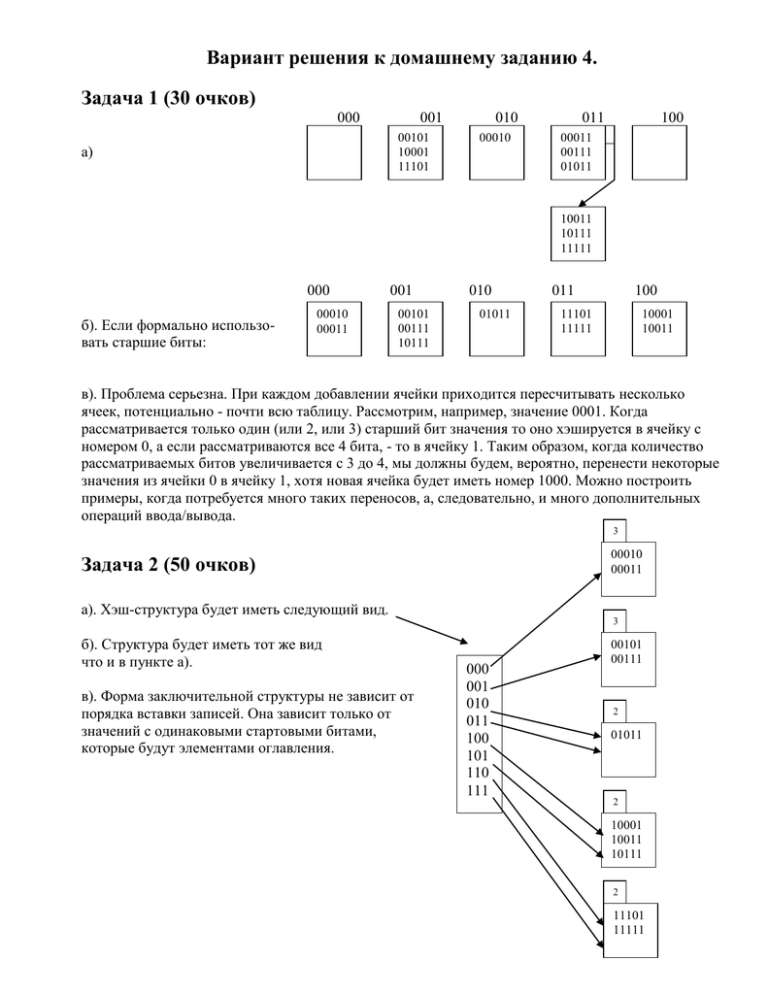
Вариант решения к домашнему заданию 4. Задача 1 (30 очков) 000 001 00101 10001 11101 а) 010 00010 011 100 00011 00111 01011 10011 10111 11111 000 б). Если формально использовать старшие биты: 00010 00011 001 00101 00111 10111 010 01011 011 100 11101 11111 10001 10011 в). Проблема серьезна. При каждом добавлении ячейки приходится пересчитывать несколько ячеек, потенциально - почти всю таблицу. Рассмотрим, например, значение 0001. Когда рассматривается только один (или 2, или 3) старший бит значения то оно хэшируется в ячейку с номером 0, а если рассматриваются все 4 бита, - то в ячейку 1. Таким образом, когда количество рассматриваемых битов увеличивается с 3 до 4, мы должны будем, вероятно, перенести некоторые значения из ячейки 0 в ячейку 1, хотя новая ячейка будет иметь номер 1000. Можно построить примеры, когда потребуется много таких переносов, а, следовательно, и много дополнительных операций ввода/вывода. 3 00010 00011 Задача 2 (50 очков) 3 a). Хэш-структура будет иметь следующий вид. б). Структура будет иметь тот же вид что и в пункте а). в). Форма заключительной структуры не зависит от порядка вставки записей. Она зависит только от значений с одинаковыми стартовыми битами, которые будут элементами оглавления. 3 000 001 010 011 100 101 110 111 00101 00111 3 2 01011 2 10001 2 10011 10111 2 11101 11111 1 00010 2 11101 00101 10001 3 00011 2 01011 10011 3 000 001 010 011 100 101 110 111 г). В случае использования старших битов структура будет иметь следующий вид. д). В этом случае проблем не возникает. Алгоритм также эввективен, как и использованный на лекции. Указатели на один и тот же блок теперь не стоят рядом, но это не снижает эффективность доступа. 11111 10111 00111 Задача 3 (20 очков) Во всех случаях число элементов оглавления будет степенью 2-ки. a). Минимальное оглавление имеет, по крайней мере, один элемент с указателем на каждую ячейку. Для 1000 ячеек, следовательно, минимальное оглавление будет иметь 1024 = 210. Для N ячеек минимальное оглавление будет иметь 2^ceil(log2(N)) элементов, где ceil() - целая часть сверху. б). Предположим, что в начальный момент у нас имеется 2 ячейки. Возможна ситуация когда при каждом добавлении ячейки ( (N-2) раза до N ячеек) нам придется удваивать размер оглавления. Например, 1-я ячейка хранит значения, начинающиеся с 0, вторая – с 10, третья – с 110, четвертая – с 1110 и т.д. N-я ячейка – с (N-1) единиц. Поскольку общее число удвоений для увеличения числа ячеек с 2 до N будет (N-2), то максимальное оглавления для 1000 ячеек может иметь 2*2998 = 2999 элементов. (что больше 10300, но меньше 10301 ).











