R = 75 Ом С = 4,3 мкФ L = 12 мГн Форма входного воздействия: U

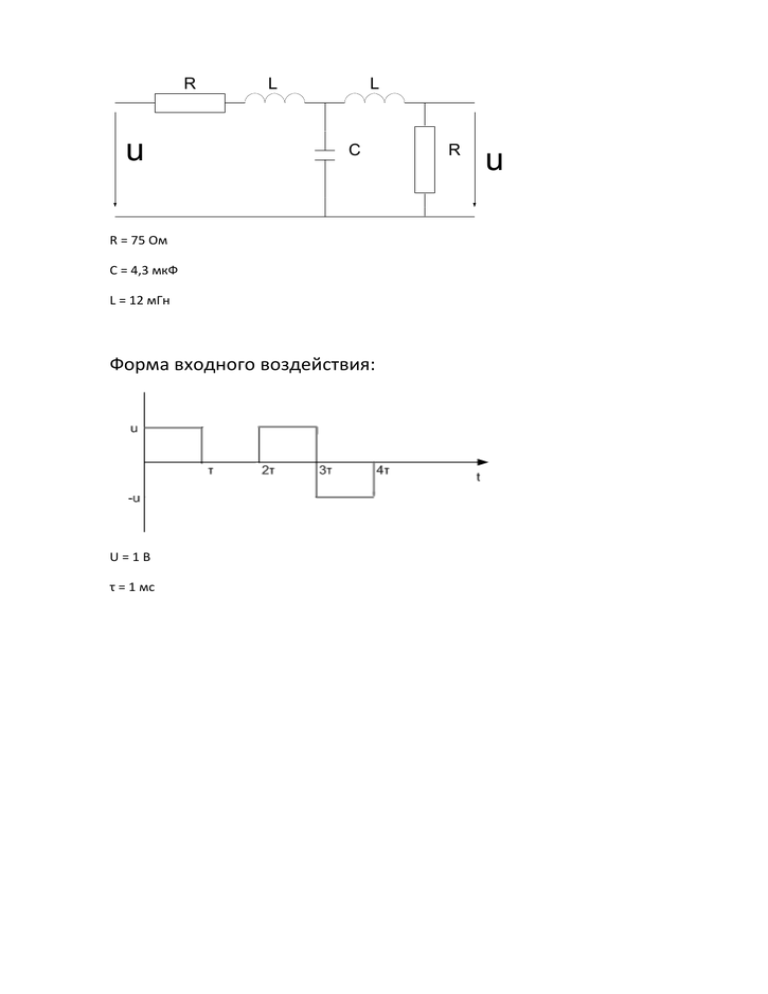
R
u
L
L
C
R = 75 Ом
С = 4,3 мкФ
L = 12 мГн
Форма входного воздействия:
U=1В
τ = 1 мс
R
u
1) Представить входное воздействие в виде линейной комбинации единичных
ступенчатых функций.
3
  10
u ( t) 
1 if t  
0 if   t  2 
1 if 2   t  3 
( 1) if 3   t  4 
0 if t  4 
2
1
u( t )
0
1
2
0
110
3
210
3
310
3
t
U(t) = 1(t )-1(t-τ)+1(t -2τ)-2*1(t-3τ)+1(t-4τ)
1, t  0
1(t )  
0, t  0
410
3
510
3
2) Определить комплексную спектральную плотность входного воздействия, построить
графики спектральных плотностей амплитуд и фаз (амплитудного и фазового спектров),
0 ≤ ω ≤ 3π/τ
Комплексная спектральная плотность входного воздействия определяется при помощи
формулы прямого преобразования Фурье. Так как u(t) = 0 при t<0, то ее можно записать
так:
Из свойства линейности преобразования Фурье следует, что комплексная спектральная
плотность сигнала U (t ) 
U (t ) может быть определена как сумма комплексных


спектральных плотностей парциальных сигналов Uv(t), т.е. Fвх ( j ) 
F ( j ) . Поэтому,


если сигналы Uυ(t) выбрать так, чтобы они удовлетворяли условию uυ(t) = aυ U(t - υτ), то с
учётом теоремы запаздывания выражение для спектральной плотности входного
воздействия можно записать в следующем виде:
Fвх ( j )  F ( j ) a  e  j

F(jω)
- комплексная спектральная плотность сигнала U(t)
A( ) 
B( ) 
sin(   )  sin( 2  )  2 sin( 3  )  sin( 4   )

1  cos (   )  cos ( 2   )  2 cos ( 3  )  cos ( 4  )

 ( )  atan


 A( ) 
B( )
2
F( )  A( )  B( )
2
4
3
2
1
 () 0
1
2
3
4
0
210
3
410
3
3
610
810
3

3
F(  )
2.510
3
2.2510
3
210
3
1.7510
3
1.510
3
1.2510
3
110
4
7.510
4
510
4
2.510
0
0
3
210
3
3
410
610

3
810
3) Определить комплексную передаточную функцию цепи, построить графики
передаточных АЧХ и ФЧХ, 0 ≤ ω ≤ 3π/τ
Комплексная схема замещения:
Составим систему уравнений по закону Кирхгофа:
i1 ( Z R  Z L )  i2 Z C  U вх
 i (Z  Z )  i Z
 3 R
L
2 C

i3 Z R  U вых


i1  i2  i3
ZR  R
Z L  jL
ZC 
1
j C
Отсюда найдем:
H ( j ) 
U вых
R

U вх (2R  2RLC 2 )  j ( 3 L2 C  2L  R 2 C )
H1( )  H( )
0.5
0.4
H1(  )
0.3
0.2
0.1
0
3
210
410
3
610
3
3
810

 ( )  arg( H( ) )
 ( )




4
3
2
1
0
1
2
3
4
0
3
210
410
3
610

3
3
810
4) Определить комплексную спектральную плотность выходного напряжения (реакции)
цепи, построить графики амплитудного и фазового спектров
0 ≤ ω ≤ 3π/τ
Fвых ( j )  Fвх ( j )  H ( j )
R(1  e  j  e 2 j  2e 3 j  e 4 j )
( 4 L2 C  2 2 L  R 2 C 2 )  j (2 R  2 RLC  3 )
Fвых ( j ) 
F1( )  Fâûõ( )
3
F1(  )
1.110
3
110
4
910
4
810
4
710
4
610
4
510
4
410
4
310
4
210
4
110
0
0
3
210
3
3
410
610
810
3

 ( )  arg( Fâûõ( ) )
4
3
2
1
 () 0
1
2
3
4
0
210
3
410
3
610

3
810
3
5) Определить функцию мгновенных значений напряжений на выходе цепи, построить
график, 0 ≤ t ≤ 6τ
Формула обратного преобразования Фурье:
1
U в ых (t ) 
2

F
в ых
( j )  e jt d

M ( p)
R(1  e  p  e 2 p  2e 3 p  e 4 p )
Fвых ( p) 

N ( p) p( p 3 L2 C  2 pL  R 2 Cp  2 R  2 RLCp 2 )
Найдем корни уравнения
N ( p)  p( p3 L2C  2 pL  R 2Cp  2R  2RLCp 2 )  0

3 2
2
p  p L C  2p  L  R C p  2 R  2R L C p

2
6250.0000000003475216


0

solve p  
 3125.0000000001710668  5384.6137208233920148i 
 3125.0000000001710668  5384.6137208233920148i 


M (0) 3 M ( p k ) pk t
U вых (t ) 

e
N (0) k 1 N ( p) p  p
k
Из найденных корней мы видим, что один из них равен 0 и два корня комплексно сопряжённых
*
Если среди корней уравнения N(p)=0 имеются комплексно сопряжённые корни pk и p k , то при
вычислении соответствующих им слагаемых в суммах выражений достаточно определить
удвоенное значение действительной части одного (любого) из этих слагаемых т.е.
*
M(p )

M ( pk ) pk t M ( p k ) pk t
e 
e  2Re  ' k e pk t 
*
'
N ( pk )
 N ( pk )

N '( p )
k
3
2
2
N( p)  p p L C  2p L  R C p  2 R  2R L C p
p1  6250
p0  0
q ( p ) 

2
p2  3125  5384.6i
R
 d N( p) 


 dp

q ( p0) 
1
2
q( p1)  0.5
q( p2)  0.29018161301504931728i
p0 t
u1( t)  q( p0)  e
u0( t) 
 q( p1)  e
p1 t

p2 t
 2 Re q( p2)  e

u1( t) if t  
( u1( t)  u1( t   ) ) if   t  2
( u1( t)  u1( t   )  u1( t  2 ) ) if 2  t  3
( u1( t)  u1( t   )  u1( t  2 )  2 u1( t  3 ) ) if 3  t  4
( u1( t)  u1( t   )  u1( t  2 )  2 u1( t  3 )  u1( t  4 ) ) if t  4
1
u0( t )
u( t )
0
1
3
210
0
410
3
t
6) Определить L-изображение входного воздействия.
U вх ( p)  U ( p) a e  p

U вх ( p) 
1
(1  e  p  e 2 p  2e 3 p  e 4 p )
p
610
3
7) Определить операторную передаточную функцию цепи, нарисовать ее нульполюсную диаграмму и операторную схему замещения цепи.
H ( p) 
U вых ( p)
R
 3 2
2
U вх ( p)
p L C  2 pL  R Cp  2R  2RLCp 2
Эта функция не имеет нулей и имеет 3 полюса:
p1 = -6250
p2 = -3125 – 5384.6i
p3 = -3125 + 5384.6i
Соответствующая нуль-полюсная диаграмма имеет вид:
8) Определить L-изображение реакции цепи, перейти от L-изображения реакции цепи к
оригиналу, построить график функции мгновенных значений напряжения на выходе
цепи, 0 ≤ t ≤ 6τ
U вых ( p)  U вх ( p)  H ( p)
R(1  e  p  e 2 p  2e 3 p  e 4 p )
U вых ( p) 
p( p 3 L2 C  2 pL  R 2 Cp  2 R  2 RLCp 2 )
p0 t
u1( t)  q( p0)  e
u0( t) 
 q( p1)  e
p1 t

p2 t
 2 Re q( p2)  e

u1( t) if t  
( u1( t)  u1( t   ) ) if   t  2
( u1( t)  u1( t   )  u1( t  2 ) ) if 2  t  3
( u1( t)  u1( t   )  u1( t  2 )  2 u1( t  3 ) ) if 3  t  4
( u1( t)  u1( t   )  u1( t  2 )  2 u1( t  3 )  u1( t  4 ) ) if t  4
1
u0( t )
u( t )
0
1
0
3
210
410
t
3
610
3
9) Определить переходную и импульсную характеристики цепи, построить их графики
0 ≤ t ≤ 6τ
h(t ) 
H ( p)
p
h (t )  H ( p)
R
p L C  2 pL  R Cp  2 R  2 RLCp 2
H ( p) 
3
2
2
R
p ( p L C  2 pL  R 2 Cp  2 R  2 RLCp 2 )
h( p ) 
3
2
Найдем оригинал этого изображения:
h( t)  q( p0)  e
p0 t
 q( p1)  e
p1 t

p2 t
 2 Re q( p2)  e

h(t) = 0.5 – 0.5e-6250t - 2*0.290e-3125tsin(5384t)
0.4
h( t )
0.2
0
0
3
3
210
410
t
3
610
Импульсная характеристика hδ(t) является реакцией цепи на входное воздействие в виде
δ-функции, изображение которой равно 1.
h (t ) 
d
h(t )
dt
h( t)  3125e
 6250t
 1812.5e
 3125t
 sin( 5384t)  3123e
 3125t
3
1.510
3
110
h( t )
500
0
0
3
3
210
410
t
3
610
 cos ( 5384t)
10) Пользуясь интегралом Дюамеля, рассчитать реакцию цепи на заданное входное
воздействие, построить график функции мгновенных значений напряжений на выходе
цепи 0 ≤ t ≤ 6τ
Реакцию цепи на входное воздействие
 f (t ) ïðè t  0
U âõ (t )  
 0 ïðè t  0
Где f(t) – функция времени, можно определить с помощью интеграла Дюамеля:
t
U âûõ (t )  f (0)h(t )   f ( )h(t   )d
0
Заданная функция входного воздействия кусочно-непрерывная, имеет пять интервалов
непрерывности:
u ( t) 
1 if t  
0 if   t  2 
1 if 2   t  3 
( 1) if 3   t  4 
0 if t  4 
U вых (t )  f1 (o)h(t )  h(t )
при 0  t  
U вых (t )  h(t )  h(t   )
при   t  2
U вых (t )  h(t )  h(t   )  h(t  2 )
при 2  t  3
U вых (t )  h(t )  h(t   )  h(t  2 )  2h(t  3 )
при 3  t  4
U вых (t )  h(t )  h(t   )  h(t  2 )  2h(t  3 )  h(t  4 )
при t  4
1
Uâûõ ( t )
u( t )
0
1
0
3
3
210
410
610
3
t
11) Сравнить результаты, полученные при анализе цепи различными методами.
Расчет цепи произведен тремя методами. Результаты анализа при различных методах
совпадают.
Московский Технический Университет Связи и Информатики
Курсовая работа по ОТЦ на тему
«Методы анализа электрических цепей
при негармоническом воздействии»
Выполнил:
Петухов А.В.
Студент группы АТ0701
Москва 2008