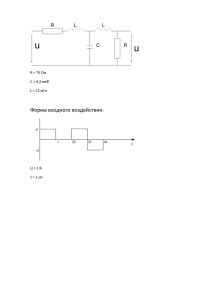
Тема лекції: Проходження сигналів через лінійні кола.

1
Лекція № 39.
Тема лекції: Проходження сигналів через лінійні кола.
1. Частотний коефіцієнт передавання ( КП ) системи.
2. Спектральний метод аналізу електричного кола.
3. Основний принцип спектрального методу.
4. Алгоритм розрахунку реакції кола для періодичних сигналів.
Література Л1 с.
Л2 с.
1. Частотный коэффициент передачи ( КП ) системы.
Запишем рассмотренное ранее выражение в виде.
U ВЫХ (t )  T  U ВХ (t )  U ВХ (t )
U ВХ (t )
-собственная функция оператора
выполняющую роль оператора
(1)
T . Определим  , как комплексную функцию,
T.
Пусть на вход воздействует сигнал в виде комплексной
экспоненты.
jt
ВХ
Тогда, в соответствии с равенствами, определяемыми интегралом Дюамеля, получается


j ( t  )
ВЫХ
ВХ


U ВХ (t )
U ВЫХ (t )
T
U
(t )   U
U


(t )  e
(t   )h( )d 
e
h( )d 
h( )e
d e
 




 j
T  k ( j )
jt
(2)
U ВХ ( t )
На основании рассмотренного последнего выражения в правой части остался неизменный
входной сигнал, как собственная функция оператора цепи, в скобках [ ] находится выражение,
описывающее этот оператор цепи. Импульсная характеристика, является оператором передачи
сигнала через цепь.

Таким образом, произведя над ней интегрирование по d , мы найдем комплексную
функцию частоты, которая тоже будет являться мерой передачи цепи на внешнее воздействие,
при том, что внешним воздействием была
 -функция.
2
h(t )
h( t )
K ( )
U ВХ
T
U ВЫХ
t
h(t )
t
Системный комплексный оператор цепи называется частотным коэффициентом передачи.
K ( j ) 

 jt
h
(
t
)
e
dt


(3)
Вывод: Импульсная характеристика цепи связанна с частотным коэффициентом передачи
стационарной системы путем прямого преобразования Фурье. Естественно , в данном случае
существует и обратный переход при помощи обратного преобразования Фурье.
1
h(t ) 
2

jt
K
(
j

)
e
d


(4)
Вывод: Прохождение сигналов через радиотехническую систему можно анализировать как
при помощи импульсной характеристики (во временной области), так и при помощи
частотного коэффициента передачи (в частотной области.). Оба подхода эквивалентны и
равноправны.
2. Спектральный метод анализа цепи.
В отличии от задач электротехники, для которой важным условием является оценка
установившегося режима, при различных коммутациях, в РТ и импульсной технике основной
задачей является воздействие данной электрической цепи, системы, на структуру сигнала.
Очевидно, например, что изменение структуры информационных импульсов может оказать
влияние на количественные и качественные показатели информации.
3
Данные задачи в РТ решаются тремя путями.
Методом анализа, использующего временные характеристики цепи ( h(t ) интеграл
Дюамеля).
2. Спектральные методы анализа.
В том числе частотные методы анализа K ( j ) , теорема о вычетах.
1.
Операторные методы анализа прохождения сигналов через цепи K ( p ) , теорема о
разложении.
3.
Суть спектрального (частотного) метода заключается в следующем: входной сигнал,
воздействующий на цепь, представляется в виде суммы гармонических составляющих,
имеющихся на входе данной системы. Сигнал на выходе будет представляться как сумму
реакций системы на каждую отдельную гармоническую составляющую. Значения
гармонических составляющих на выходе легко найти, если известен частотный коэффициент
передачи и ряд Фурье, описывающий сигнал на входе.
Т.к. в основе спектрального анализа лежит принцип суперпозиции, то такой метод является
линейным и он справедлив для линейных систем.
3. Основной принцип спектрального метода.
Пусть на входе действует сигнал, заданный ОПФ.
1
U ВХ (t ) 
2

 ( )e jt d
U
 ВХ

(5)
Предположим, что известен частотный коэффициент передачи данной системы K ( j ) .
jt
Из приведенных выше рассуждений комплексный сигнал вида e
, является собственной
jt
функцией системного оператора, создавая на выходе реакцию
на
K ( j )e
элементарное воздействие (  -функция). Суммируя эти реакции, найдем представление
выходного сигнала.
1
U ВЫХ (t ) 
2

jt
K
(
j

)
U
(

)
e
d
ВХ


(6)
Данная формула является основной формулой спектрального анализа.
Данное выражение позволяет найти реакцию цепи на любое входное воздействие, используя
частотную характеристику цепи. Полученное выражение показывает значение оператора цепи
K ( j )
как коэффициента пропорциональности между спектральными плотностями
входного и выходного сигналов.
4
U ВЫХ ( )  K ( j )U ВХ ( )
(7)
Тем самым, показывая простоту решения задач в частотной области, которая сводится к
обычной операции умножения.
4. Алгоритм расчета реакции цепи для периодических сигналов.
Для определения алгоритма расчета реакции цепи для периодических сигналов
U ВХ (t )
Сначала необходимо разложить заданный сигнал в
ряд Фурье.
1.
T
a 0 
S ВХ (t ) 
  An ВХ cos( n 1 t   0 )
2 n 0
t
2

(8)

Для заданной цепи находится частотный коэффициент передачи K ( j ) . Данный
частотный коэффициент передачи дискретизируется по оси частот с шагом дискретизации
2.
n1
( K (n1 )) .
Рассчитывается реакция цепи на сумму входных гармонических воздействий ,
представленных рядом Фурье. Выходная реакция определяется как сумма произведения
амплитуды каждой из гармоник, умноженной на конкретной частоте.
3.
AnВЫХ (n1 )  K (n1 ) AnВХ (n1 )
(9)
 ВЫХ   ВХ   K ( )
U ВЫХ (t ) 
a 0 ВЫХ
2
(10)

  An ВЫХ ( n 1 ) cos( n 1 t   ВЫХ )
n 0
Пример.
I
U ВХ (t )
R
Um
U ВХ (t )
T
2

t
C
U ВЫХ (t )
(11)
5
u
1.
2
a0 1

2 T
 Umdt 

u
Um
q
2
u
2.
2
an 
T
bn  0
2
 Um cos n1tdt 

u
2Um

q
n 1
2
An  a n2  bn2 
3.
tu
2
sin n 1
2Um

q
tu
2
sin n 1
n 1
tu
2
tu
2
tu
sin n 1
Um 2Um 
2 cos n t
S (t ) 


1
tu
q
q n 0
n 1
2
1
K ( ) 
U ВЫХ (t )

U ВХ (t )
jc
1
1


1
1  jRC 1  j
R
jc
U ВЫХ (t )  IR ВЫХ
1
I
jC
U ВХ (t )  IR цепи
  RC
1
 I (R 
)
jC
6
Представим данный коэффициент передачи в показательном виде. Модуль
арка цепи,
K ( ) -это АЧХ-
arctg ( ) - показатель степени экспоненты - это ФЧХ цепи.
K ( )  K ( ) e
K ( ) 
K ( )
 jarctg ( )
1
1  ( ) 2
0,1
1  2  3  4  5  6  ср
RC -цепь данного типа является ФНЧ.
Рассчитываем дискретный коэффициент передачи нашей цепи.
K ( n 1 ) 
1
12  ( n 1 ) 2
2
1 
TВХ
Записать ряд Фурье для выходного сигнала.
AnВЫХ (n1 )  K (n1 )  AnВХ (n1 )
tu
sin
n

1
2Um
1
2
AnВЫХ ( n1 ) 

2
tu
q
1

(
n


)
1
n1
2
a0
a0
Um
1
ВЫХ 
K ( n 1 ) 
2
2
q 1  ( n 1 ) 2
7
sin n 1
2Um 
S ВЫХ (t ) 


1
t
q n 0
q 1  ( n 1 )
n 1 u
2
 cos( n 1 t  arctg ( n 1 ))
Um
tu
2
1
1  ( n 1 )
2

На следующем этапе выполняем синтез гармонических составляющих на выходе, амплитуды
которых равны
AВЫХ (n1 ) .
U ВЫХ (t )
u
t