1. Основна формула.

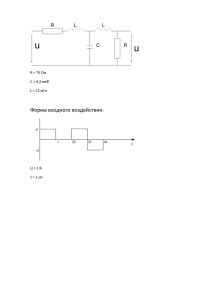
1
Лекція 40
Тема: Загальний підхід до спектрального методу при проходженні
неперіодичних сигналів через електричне коло.
1. Основна формула.
2. План розрахунок проходження неперіодичних сигналів через РТ-кола.
3. Основні положення теореми про розкладання.
4. Теорема про розкладання з нульовим коренем.
5. Теорема про розкладання без нульового кореня.
6. Поняття комплексної частоти.
7. Основні співвідношення.
8. Розрахунок реакції кола на проходження прямокутного відеоімпульсу через
RC- коло.
9. Розрахунок реакції ланцюга на проходження експоненціального
відеоімпульсу через RC-коло
1. Основная формула.
При расчете прохождения непрерывных сигналов спектральным методом
используется прямое и обратное преобразования Фурье. Представление
непрерывных функций в виде интеграла Фурье подразумевает суммирование
бесконечного числа незатухающих и бесконечно близких друг к другу по
частоте гармонических колебаний с бесконечно малыми амплитудами.
1
U ВЫХ (t ) 
2

 ( )e jt d
K
(
j

)
U
ВХ


Следует отметить ограничения, накладываемые на частотный коэффициент
передачи цепи.
Не каждый коэффициент передачи можно реализовать в физических системах.
Для того чтоб
двух условий.
K ( j ) был полностью реализуем необходимо выполнение
На основании свойств преобразования Фурье K ( j )  K (  j ) . Т.е.
модуль коэффициента передачи должен быть четной функцией, а аргумент
коэффициента передачи- нечетной.
2. На основании доказательства теоремы Винера о физической реализуемости
частотных характеристик важнейшим условием их реализуемости является
условие:

*
1.
K ( j )
 1

2
d  
2
Пример.
?   СР     СР
K ( j )  
0     СР ,  СР 
Пусть
h(t )
Попробуем найти
1
h( t ) 
2

K 0 СР

 СР
 K

0
e
jt
K ( j )
d 
h(t )
СР
sin  СР
 СР
tu
2
tu
2
  СР
 СР

0
Рассмотрев ИХ видно, что она уходит в бесконечность, тогда не выполняются
ограничения, накладываемые на импульсную характеристику, а значит
предложенный коэффициент передачи нереализуем.
2.План расчет прохождения непериодических сигналов
через радиотехнические цепи.
1.
Если есть U ВХ (t ) , то необходимо найти его спектральную плотность.

U ВХ ( )   U ВХ (t )e  jt dt

2.
3.
Необходимо найти коэффициент передачи цепи K ( j ) .
Находим спектральную плотность сигнала на выходе.
U ВЫХ ( )  K ( j )U ВХ ( )
4.
находим реакцию цепи на выходе U ВЫХ (t ) .
1
U ВЫХ (t ) 
2

jt

U
(

)
e
d
 ВЫХ

Однако нахождение обратного преобразования Фурье и спектральной
плотности выходного сигнала в большинстве случаев задача сложная т.к.
U ВЫХ ( ) будет иметь сложный
вид. Поэтому.
t
3
Возможно применение теоремы о вычетах в частотной области.
2. а) переход к лаплассовским частотам, и взятие обратного преобразования
Лапласа. Однако и данная задача может быть невыполнима, тогда.

pt
ВЫХ
ВЫХ

б) переход к лаплассовским частотам и использование теоремы о
разложениях.
1.
1
(t ) 
2
U
U
( p )e dp
3. Основные положения теоремы о разложениях.
При сложном нахождении оригинала S ВЫХ (t ) путем решения ОПФ или
обратным преобразованием Лапласа возможно использование теоремы о
разложениях. Для использования теоремы о разложениях необходимо перейти
из комплексной плоскости к лаплассовской p    j частоте, при чем
Re p примем равной нулю.
S ( )  входная
1.
2.
3.
K ( j )
S ВЫХ ( j )  K ( j )S ВХ ( j )
S ВЫХ ( p)  S ВЫХ ( j )
4.
5.
Теорема о вычетах
Запишем отношение изображений входного и выходного сигналов.
K ( p) 
U ВЫХ ( р )
U ВХ ( p ) - передаточная функция цепи.
Для решения любой задачи операторный (частотный) коэффициент передачи
нужно представить в каноническом виде.
K ( p) 
Функция
K ( p)
bm p m  bm1 p m1  ...  b1 p 1  b0 p 0
a n p n  a n 1 p n 1  ...  a1 p 1  a 0 p 0
аналитическая на всей плоскости за исключением точек
pi ( p1 , p 2 ,..., p n ) , являющихся корнями знаменателя коэффициента
передачи системы. Функция не будет аналитична в точках, удовлетворяющих
решению уравнения.
Корни
a n p n  a n 1 p n 1  ...  a1 p 1  a 0 p 0  0
p1 , p2 ,..., pn , называются полюсами передаточной функции.
4
Рассмотрим частный случай, когда
U ВЫХ ( p) представляет собой отношение
двух многочленов с указанными степенями
m и n.
M ( pi )
U ВЫХ ( p )  K ( p )U ВХ ( p ) 
N ( pi )
При чем будем считать, что степень числителя не превосходит степень
n
знаменателя
, кроме того, корни знаменателя должны быть простые и
отрицательные.
Способ нахождения оригинала основывается на представлении функции
U ВЫХ ( p) в виде суммы элементарных дробей.
K
Ci
U ВЫХ ( p )  
i 1 p  pi
,где
Ci
является вычетом функции
U ВЫХ ( p) в точках с полюсами p i .
4. Теорема о разложении с нулевым корнем.
M (0) K M ( pi ) pi t
U ВЫХ (t ) 

e
N ' (0) i 1 N ( pi )
Притом, что U ВЫХ ( p ) в виде суммы элементарных дробей была
представлена в виде.
K
U ВЫХ ( p )  
i 1
M ( pi )
N ' ( pi ) p( p  pi )
11.5 Теорема о разложении без нулевого корня.
K
M ( pi ) pi t
U ВЫХ (t )  
e
i 1 N ( pi )
K
M ( pi )
U ВЫХ ( p )  
при
i 1 N ' ( pi ) p( p  pi )
6. Понятие комплексной частоты.
Спектральные методы, как уже известно, основаны на том, что исследуемый
сигнал представляется в виде суммы неограниченно большого числа
5
элементарных слагаемых, каждое из которых периодически изменяется во
времени по закону exp( jt ) .
Естественно обобщение этого принципа заключено в том, что вместо
комплексных экспоненциальных сигналов счисто мнимыми показателями
вводят в рассмотрение экспоненциальные сигналы вида
exp( pt ) , где
p  комплексное число: p    j , получившее название комплексной
частоты.
Из двух таких комлексных сигналов можно составить вещественный сигнал,
например, по следующему правилу:

pt
p *t
1
S (t ) 
e e
2

(1)
где p    j комплексно-сопряженная величина.
Действительно, при этом
*
e jt  e  jt
S (t )  e
 e t cos t
2
t
(2)
В зависимости от выбора вещественной и мнимой частей комплексной частоты
можно получить разнообразные вещественные сигналы. Так, если   0 , но
  0 , получаются обычные гармонические колебания вида cos t . Если
же   0 , то в зависимости от знака  получаются либо наростающие, либо
убывающие во времени экспоненциальные колебания. Более сложную форму
такие сигналы приобретают, когда   0 . Здесь множитель exp(t ) описывает
огибающую, которая экспоненциально изменяется во времени. Некотрые
типичные сигналы изображены на рисунке.
  0,  0
  0,   0
t
t
  0,  0
t
  0,  0
t
6
Понятие комплексной частоты оказывается весьма полезным прежде всего
потому, что это дает возможность, не прибегая к обобщенным функциям,
получать спектральные представления сигналов, математические модели
которых неинтегрируемы. Существенно и другое соображение:
экспоненциальные сигналы вида (2) служат «естественным» средством
исследования колебаний в разнообразных линейных системах.
Следует обратить внимание на то, что истинная физическая частота  служит
мнимой частью комплексной частоты. Для вещественной части 
комплексной частоты специального термина не существует.
7. Основные соотношения.
Пусть f (t )  некоторый сигнал, вещественный или комплексный,
определенный при t  0 и равный нулю при отрицательных значениях
времени. Преобразование Лапласа этого сигнала есть функция комплексной
переменной p , задаваемая интегралом:

F ( p)   f (t )e  pt dt
(3)
0
Сигнал f (t ) называется оригиналом, а функция F ( p )  его изображением по
Лапласу.
Условие которое обеспечивает существование интеграла (3), заключается в
следующем: сигнал f (t ) должен иметь не более чем экспоненциальную
степень роста при t  0 , т.е. должен удовлетворять неравенству
f (t )  A exp( at ) , где A, a  положительные числа.
При выполнении этого неравенства функция F ( p ) существует в том смысле,
что интеграл (3) абсолютно сходится для всех комплексных чисел
p ,у
которых Re p  a . Число a называют абсциссой абсолютной сходимости.
Переменная p в основной формуле (3) может быть отождествлена с
комплексной частотой p    j . Действительно, при чисто мнимой
комплексной частоте, когда   0 , формула (3) переходит в формулу
S ( ) 

 jt
s
(
t
)
e
dt


определяющую Фурье-преобразование сигнала, который равен нулю при
t  0 . Таким образом, преобразование Лапласа можно рассматривать как
обобщение преобразования Фурье на случай комплексных частот.
Подобно тому, как это делается в теории преобразования Фурье, можно, зная
изображение, восстановить оригинал. Для этого в формуле обратного
преобразования Фурье
7
1
f (t ) 
2

 F ( )e
jt
d

следует выполнить аналитическое продолжение, перейдя от мнимой
переменной j к комплексному аргументу   j . На плоскости
комплексной частоты интегрирование проводят вдоль неограниченно
протяженной вертикальной оси, расположенной правее абсциссы абсолютной
1
 dp ,
d


сходимости. Поскольку при   const дифференциал
 j
формула обратного преобразования Лапласа приобретает вид
c  j
1
f (t ) 
F ( p)e pt dp

2j c  j
(4)
В теории функций комплексного переменного доказано, что изображения по
Лапласу обладают «хорошими» свойствами с точки зрения гладкости: такие
изображения во всех точках комплексной плоскости p за исключением
счетного множества так называемых особых точек, являются аналитическими
функциями. Особые точки, как правило, -полюсы, однократные или
многократные. Поэтому для вычисления интегралов вида (4) можно
использовать гибкие методы теории вычетов.
На практике широко применяются таблицы преобразований Лапласа, в которых
собраны сведения о соответствии между оригиналами и изображениями.
11.8 Расчет реакции цепи на прохождение прямоугольного видеоимпульса
через RC-цепь.
I
U ВХ (t )
R
U ВЫХ (t )
C
U ВЫХ (t )

U ВХ ( j ) 

 Ume
 jt
dt  Um  t u

1.
 Um  t u
e
j
tu
 j
e
t
2 j u
2
2
tu
2
tu
2
tu
2
sin 

tu
2
tu
2 
t
8
2.
3.
1
r
( j )
jC
1
K ( j )  ВЫХ


1
rВХ ( j )
1  j
R
jC
t
 j tu
 j u
Umtu  e 2  e 2
U ВЫХ ( j ) 

t
2 
j u

2
t
 p tu
p u
Umtu  e 2  e 2
U ВЫХ ( p ) 

t
2 
p u
2

4.
t
 p tu
p u
2Umtu  e 2  e 2


2tu  p ( p  1 )




1


 1  j



1



1

p








Приравниваем значение знаменателя к нулю для нахождения корней.
p1  0
p
1
 0  p2  

t
t

pi u
 p1 u
Um N  e 2  p 2
U ВЫХ (t ) 

 i 1  ( p  p i )'

1


  e pi t 


Хотя система и имеет корень с нулевым решением, однако для нашего случая
явно видно, что
M (0 )
N (0 )
обращается в ноль.
N ' ( pi )  ( p  pi )'  1
9
t
t
t
t
1
1

 (t  u )
(t  u ) 
 pi ( t  u ) 
Um  pi ( t  2u )
Um
2

e
e  2  e  2 
e

 
  

9. Расчет реакции цепи на прохождение экспоненциального видеоимпульса
через RC-цепь.
U ВХ (t )  Ume t
t
1.
2.
3.
U ВХ ( j )   Ume
K ( j ) 
t
e
 jt
Um
dt 
  j
1
1  j
U ВЫХ ( j ) 
Um
(  j )(  j )
Um
U ВЫХ ( p ) 

(  p )(  p )
Um
1
 ( p   )( p  )

10
p1    0
p2 
1

0
M ( pi )  1
1
N ( p i )  ( p  p1 )( p  p 2 )
p1  
p2  
i
2

N ' ( p )  ( p  p )  ( p  p1 )  2 p  p 2  p1
Ume p1t
1
Ume p2t
1
U ВЫХ (t ) 
 
 
2 p1  p2  p1  2 p2  p2  p1 
Um
 
e p1t
p1  p2
Um
e p2t
1
 t
 t
Um


e

e



p2  p1  (  1 ) 
 1  
 
Um

t
 
 t

e  e 


U ВЫХ (t )
t
10. РАСЧЕТ ВЫХОДНОГО НАПРЯЖЕНИЯ ПРИ ГАРМОНИЧЕСКОМ
ВОЗДЕЙСТВИИ.
Входной сигнал существует с момента t = 0 и имеет вид
UBX (t) = Um sin ωot ·σ(t).
Изображение этого сигнала будет представлено формулой
U BX ( p) 
U mo
p 2  o2
Передаточная функция рассмотренной выше цепи равна:
1

K ( p) 

1  p
p 
где α = 1/τ, следовательно
U вых ( p) 
U mo
( p   )( p 2  o2 )
По таблицам находится временное изображение выходного сигнала.
11
U вых (t ) 

U mo  t

e

cos

t

sin

t
o
o


o
 o2   2 

Первое слагаемое в квадратных скобках правой части отображает
затухающий свободный процесс. Если αt » 1, то в решении остается лишь
вынужденная составляющая, которая изменяется во времени по гармоническому закону.
11. Расчет отклика последовательного контура на ступенчатую фукцию.
Рассмотрим известную электрическую цепь в виде последовательного
колебательного контура.
Передаточная функция имеет вид
 o2
1 /  pC 
K ( p) 
 2
pL  R  1 /( pC ) p  2  p   o
,
где α = R/(2L).
Входной сигнал – функция Хевисайда (ступенчатая функция) с
изображением 1/р.
Следовательно, изображение выходного сигнала имеет вид
12
U ВЫХ ( p) 

 o2
p  p      c2
2
.
Используя таблицу преобразований Лапласа, находим окончательно
g (t )  1  e  t (cos ct 

sin ct )
c
График функции g(t) указывает на то, что под действием единичного скачка
напряжение на входе система совершает колебательные движения, асимптотически стремясь к новому стационарному состоянию.
Выводы
1.Закон, связывающий входной и выходной сигнал в системе, называется
системным оператором.
2.Классификация систем основана на свойствах системных операторов.
Различают линейные и нелинейные, стационарные и нестационарные,
сосредоточенные и распределенные системы.
3.Реакция линейной системы на дельта-импульс называется импульсной
характеристикой.
4.Сигнал на выходе есть свертка входного сигнала и импульсной
характеристики. Частотный коэффициент передачи и импульсная
характеристика связаны парой преобразований Фурье.
5.Собственные колебания динамических систем определяются корнями
характеристического уравнения.
6.Частотный коэффициент передачи линейной стационарной системы,
описываемой обыкновенным дифференциальным уравнением, есть дробнорациональная функция частоты.
7.Спектральная плотность выходного сигнала является произведением
частотного коэффициента передачи и спектральной плотности колебания на
входе.