Решение задач с помощью линейных уравнений

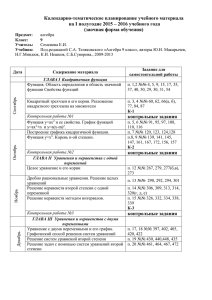
Решение задач с помощью линейных уравнений. 7 класс.
Методическая разработка учителя математики Нарвской Кесклиннаской гимназии
Авраменко Владиславы.
Основным средством воспитания и развития математических способностей учащихся
являются задачи. Не случайно известный математик и методист Д.Пойа пишет: «Что
значит владение математикой? Это есть умение решать задачи, причём, не только
стандартные, но и требующие известной независимости мышления, здравого смысла,
оригинальности, изобретательности.»
Для учителей математики не секрет, что как раз научить решать учеников задачи является
делом нелёгким, а уж составить по условию задачи уравнение вообще для некоторых
семиклассников (и не только) – высший пилотаж, тем более что времени на эту тему
отводится немного, да и логическое мышление у современных учеников развито слабо. А
ведь решаем задачи с помощью уравнений начиная уже с 4-5 класса второй ступени, и
всегда в материалах экзамена по математике за курс основной школы такая задача
имеется. Поэтому и приходится придумывать такие способы объяснения нового
материала, чтобы большинству учащихся с разными математическими способностями
было понятно.
Я попробовала разделить все задачи по составлению уравнений на четыре основных типа:
1) задачи, где в условии сказано, что величины равны;
2) задачи, где в условии сказано, сколько всего или вместе;
3) задачи, где в условии сказано, что одна величина больше (меньше) другой на
какое-либо число;
4) задачи, где в условии сказано, что одна величина больше (меньше) другой во
сколько-то раз.
Вместе с учениками мы схематически изображаем, как составить уравнение для всех этих
основных типов задач.
К первому типу:
I
=
II
(поровну)
Ко второму типу:
I
+
= вместе
II
К третьему типу:
Большее
=
Меньшее
+ НА…
К четвёртому типу:
Большее
=
Меньшее
*
В…
Такие схемы упрощают составление уравнения к задаче. По своему условию можно
задачи объединять в группы, например, мы с ребятами в отдельные группы определили
1) задачи на движение; 2) задачи на определение стоимости (ученики их назвали
«задачами про магазин»); 3) задачи на «перекладывание» - к ним ребята отнесли те задачи,
в которых говорится о том, что например, из одного хранилища увозят, в другое привозят,
или из одной корзины берут, в другую добавляют, т.е. изменение количества; 4) задачи ,
где условие записывается в виде схемы, например, про 3 угла треугольника, про 3 полки, 4
цеха и т.д.; 5)задачи на совместную работу. Конечно, задач гораздо больше, но если
ученики усвоят хотя бы эти основные типы, у них уже есть основа для составления
уравнений к задачам в 8,9 классах, и конечно, в гимназии.
Для задач на движение, стоимость и «перекладывание» очень удобно, на мой взгляд,
составлять таблицу, рассматривая две ситуации или два объекта к задаче. Приведу
некоторые примеры, как мы с ребятами 7 класса оформляем задачи на составление
линейных уравнений.
Задача №1.
Расстояние между городами 230 км. Одновременно навстречу друг другу из городов
выезжают два автомобиля. Скорость одного из них 50км/ч, скорость второго 65км/ч.
Через сколько часов автомобили встретятся?
Объект
1 автомобиль
2 автомобиль
Время
(ч)
х
х
Скорость(км/ч) Расстояние
(км)
50
50х
65
65х
ВМЕСТЕ 230км
Составим уравнение по второй схеме: 50х+65х=230 , откуда х=2.
Задача №2.
На первом участке в 3 раза больше кустов, чем на втором. Когда с первого участка
выкопали 50 кустов, а на второй посадили ещё 20 кустов, то на первом участке стало на
300 кустов больше, чем на втором. Сколько кустов было на каждом участке
первоначально?
Объект
1 участок
2 участок
Было
(саж.)
3х
х
Что сделали
(саж.)
-50
+20
Стало (саж.)
3х-50
х+20
Больше
Меньше
на 30 кустов
Составим уравнение по нашей третьей схеме: 3х-50= (х+20)+30 , откуда х=50 (это на
втором участке), а на первом было 150 кустов первоначально.
Задача №3. Один угол треугольника в 3 раза больше второго, а третий угол на 540 больше
первого. Найдите углы треугольника.
Первый угол
3х
Второй угол
х
Всего 1800
0
Третий угол
3х+ 54
Составим уравнение к задаче: 3х+х+(3х+540)=1800, откуда углы треугольника 540, 180 и
1080 соответственно.
Систематическая работа по изучению способов решения задач помогает учащимся не
только научиться решать задачи, но и самим их составлять. Я предлагаю учащимся в
конце изучения этой темы сделать творческую работу с использованием презентации,
составив свою задачу. Ученики составляют задачи практического содержания, которые
можно потом использовать на уроках с другими школьниками. Причём, на защите своей
работы автор предлагает классу решить его задачу и сам проверяет решение (после того,
как авторские работы проверены мною). Отрабатывая таким образом решение задач,
надеюсь, что в старших классах ребятам будет легче составлять уже квадратные или
дробные уравнения к задачам, тем более что все четыре схемы работают и для этих
уравнений.