закон сохранения момента импульса. определение момента

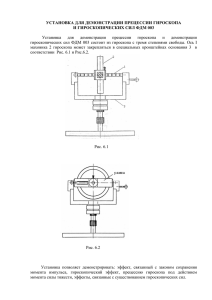
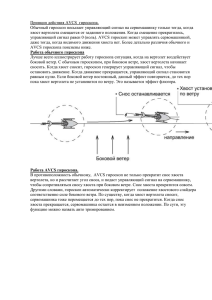
Приднестровский государственный университет
им. Т.Г. Шевченко
Лабораторные работы
по курсу общей физики
раздел 1: МЕХАНИКА
Лабораторная работа №1.08
Тема: ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ГИРОСКОПА
Кафедра ОФ и МПФ
Тирасполь - 2006
ЛАБОРАТОРНАЯ РАБОТА № 1.08
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА.
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ГИРОСКОПА
Цель работы: Изучение движения гироскопа, вращающегося вокруг
горизонтальной оси в поле силы тяжести.
Приборы и принадлежности: Установка, состоящая из гироскопа,
насаженного на вертикальную ось и дополнительные грузы массой в100 и
200г. Установка снабжена электросекундомером и измерителем угла
поворота.
КРАТКАЯ ТЕОРЕТИЧЕСКАЯ СПРАВКА
А.Согласно определению момент импульса твёрдого тела равен:

 
L =  r p  . Для симметричного тела, вращающегося вокруг оси симметрии,



проходящей через центр масс эта формула преобразуется к виду: L  I , где

I момент инерции тела,  -угловая скорость вращения. Такое тело называют
гироскопом или волчком. Если гироскоп находится во внешнем
гравитационном поле, то на него действует ещё момент силы


M  r F  (1)
В этом случае необходимо применить основной
закон динамики для

dL

 M (2),
вращающегося твёрдого тела:
dt
  
где M  l mg - момент силы тяжести гироскопа относительно его точки
опоры О. Рассмотрим два частных случая: 1) ось гироскопа вертикальна

(параллельна вектору ускорения свободного падения g ) и 2) ось гироскопа

составляет угол  c направлением вектора g . Рассмотрим первый случай


(рис.1). Угол  между вектором r и mg равен  (ось гироскопа вертикальна)



dL
 0 . В этом случае L  const . Тогда
и M  rmg sin   0 . Следовательно
 
dt
направление оси вращения и угловой скорости (в отсутствии сил трения)
остаются постоянными. При наличии сил трения гироскоп со временем
потеряет кинетическую энергию вращения и опрокинется. Рассмотрим
второй случай: когда угол  острый (рис.2). Тогда на гироскоп действует
M,
опрокидывающий
момент
модуль
которого
равен

M  rmg sin   0 (рис.2) Действующий момент стремится опрокинуть
гироскоп. По правилу буравчика он направлен от нас за чертёж. Как
показывает опыт, ось гироскопа начинает
прецессировать вокруг

вертикальной оси с угловой скоростью  и не опрокидывается. Если
прецессию оси гироскопа остановить, то гироскоп упадёт. Таким образом,
прецессия оси гироскопа связана с появлением восстанавлюющего момента,
который противоположен опрокидующему моменту. Эти два момента равны
-2-


по абсолютной величине M  M вост и противоположны по направлению.


M  M вост Этим объясняется то, что гироскоп, несмотря на наклонное
положение своей оси, не опрокидывается.

 


dL
 M вост  L
dt
(3)
Исходя из равенства моментов, следует равенство их модулей:
rmg sin(   )  L sin  .
В. Рассмотрим случай горизонтального гироскопа, вращающегося в
подшипниках А и В


Момент импульса гироскопа L  I , где I  момент инерции. Любая
турбина, находящаяся на корабле может служить таким гироскопом. При
изменении курса корабля турбина целиком повернётся
вокруг вертикальной

оси с некоторой угловой скоростью
 . Поэтому появится
восстанавливающий момент. Этот момент будет стремиться
повернуть


вектор I гироскопа так, чтобы его совместить
с вектором  . В этом случае


на подшипники подействует пара сил Q и  Q . При больших  эта пара сил
вполне может разрушить подшипники (рис.3).

 
I  l Q ,
(4)

  
где l - плечо силы Q.

  
В данном случае   I и l  Q . Поэтому найдём Q в скалярном виде:
Q
I
l
Давление Q на подшипники зависит от угловой скорости  и при
резком повороте корабля давление может стать столь большим, что может
разрушить подшипники.
Для измерения гироскопических эффектов используется установка
FRM-10, оборудованная счетчиком периодов,
счетчиком времени и
счётчиком угла поворота.
Гироскоп установлен так, что он может вращаться вокруг осей z и у и
поворачиваться на небольшие углы вокруг оси х.
1) Ось z направлена по оси гироскопа и проходит через центр инерции
оси подвески электродвигателя.
2) Ось у перпендикулярна горизонтальной плоскости и направлена
вертикально вверх.
3) Ось х находится в горизонтальной плоскости и проходит через центр
инерции оси подвески электродвигателя.
Система х, у, z составляет правую систему координат (рис.3 ).
На оси гироскопа находится небольшой груз (m=375г) для
горизонтального установления оси гироскопа. На левый рычаг оси гироскопа
можно добавлять перегрузки, имеющие массы 100г и 200г. В результате
-3-
появится дополнительный момент, действующий на гироскоп, что приводит

к появлению прецессии гироскопа в горизонтальной плоскости с частотой  .

 
Из условия M вост  I можно вычислить I :



M в ост
I=  
 


(7)
Методика проведения эксперимента
1) Уравновесить гироскоп так, чтобы ось гироскопа z была
горизонтальна.
2) Включить питание электродвигателя.
3) Установить число оборотов двигателя 6000об/мин.
4) На левое плечо на расстоянии l от центра инерции поместить
перегрузок массой m=100г.
5) Нажать кнопку «сброс» и после того как гироскоп повернётся в
горизонтальной плоскости на угол примерно 300 нажать кнопку «стоп».
6) С помощью линейки измерить расстояние l от центра инерции Ц до
центра дополнительного груза.
7) Вычислить угловую скорость  

t
времени и прецессии.
8) Зная  ,  и поставляя в (7) выражение:
по показателям приборов
 
 

M вост  l mg
определить момент инерции I по формуле (8) (опыт сделать 3 раза):
I 
lmg 
   
(8)
9) Повторить опыт с перегрузком грузом массой 200г три раза при двух
угловых скоростях  гироскопа (6000 и 5000 об/мин) и записать данные в
таблицу.
№
Данные наблюдений
m,
r,м  ,рад
,
кг
рад/c
Результаты расчетов
t ,с  ,рад/c l ,м I ,кг.м2 I ,кг.м2  %
1
2
3
Ср.
знач.
Конечный результат записать в данной форме: I  I cp  I
-4-
Контрольные вопросы
1.Момент силы. Направление момента силы. Единицы измерения.
2.Основной закон динамики для вращающего твёрдого тела.
3. Прецессия гироскопа. Восстановляющий момент.
4. Момент инерции гироскопа. Единицы измерения момента инерции.
5. Момент импульса тела относительно точки и оси.
6. Закон сохранения момента импульса.
Литература:
1.
В.И. Иверонова. Физический практикум. Лаб. работа № 17. Тема:
изучение движения гироскопа.
-5-
l
 
 
  
M  l mg

 
М вост  I