Суперпозиция сил

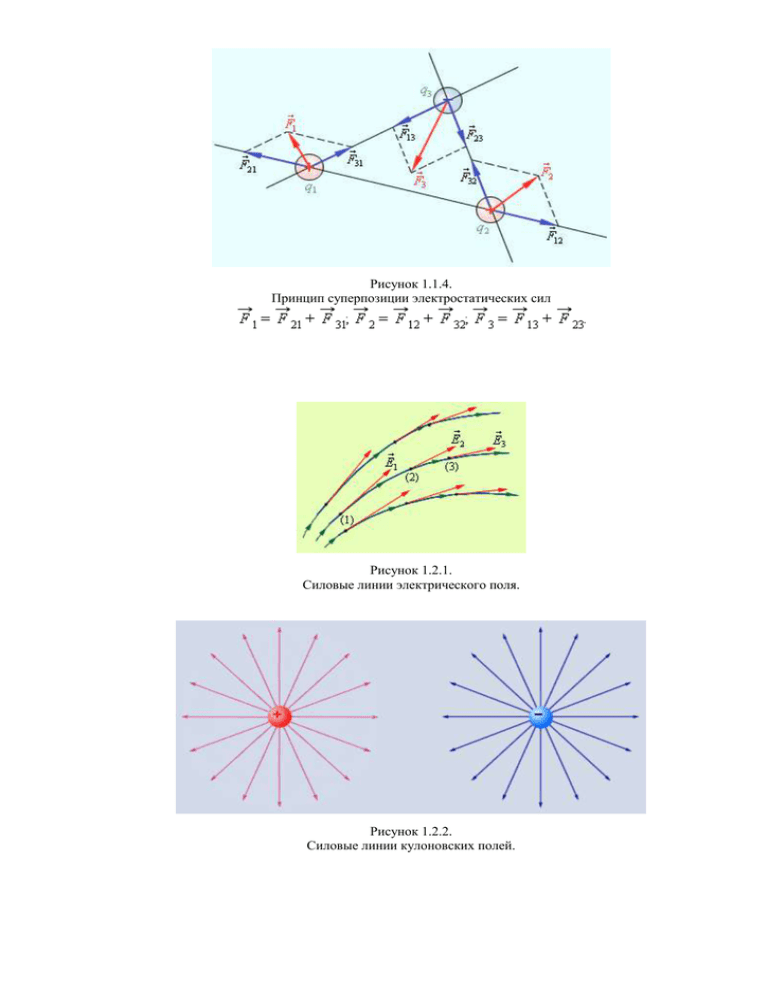
Рисунок 1.1.4.
Принцип суперпозиции электростатических сил
Рисунок 1.2.1.
Силовые линии электрического поля.
Рисунок 1.2.2.
Силовые линии кулоновских полей.
Рисунок 1.2.3.
Силовые линии поля электрического диполя
Рисунок 1.2.4.
Дипольный момент молекулы
воды.
Рисунок 1.2.5.
Электрическое поле заряженной нити.
Модель. Электрическое поле точечных зарядов.
Модель. Движение заряда в электрическом поле.
Рисунок 1.3.1.
К определению элементарного потока ΔΦ.
Рисунок 1.3.2.
Вычисление потока Ф через произвольную замкнутую
поверхность S.
Рисунок 1.3.3.
Поток электрического поля точечного заряда через
произвольную поверхность S, окружающую заряд.
Рисунок 1.3.4.
Вычисление поля однородно заряженного
цилиндра. OO' – ось симметрии.
Рисунок 1.3.5.
Поле равномерно заряженной плоскости. σ –
поверхностная плотность заряда. S –
замкнутая гауссова поверхность.
Если результирующее поле образовано наложением нескольких
полей, то результирующая напряженность равна векторной сумме
напряженностей каждого поля:
E=E(1) +E(2)+…
Пусть в точке 2 потенциал выбран равным нулю. Тогда из
очевидных равенств
2
2
2
2
1
1
1
1
  1 2   Ed r   ( E (1)  E ( 2 )  ...)d r   E (1) d r   E ( 2 ) d r  ...  (1)  ( 2) ...
следует, что потенциал в произвольной точке равен сумме
потенциалов всех полей, образующих результирующее поле.
Конечно, это прямое следствие принципа суперпозиции.
Докажем, что электростатическое поле потенциально, т. е.
разность потенциалов между точками 1 и 2 не зависит от
траектории, по которой происходит перемещение заряда из точки 1
в точку 2. Пусть поле создается только одним точечным зарядом Q.
Тогда по определению разности потенциалов
1
2
2
1
 1 2   Edr  
r
dr
4 0 r 3
Q
Скалярное произведение (r dr) = |г|  |dr|  cos а равно r  dr —
произведению расстояния r до заряда на приращение этого
расстояния dr (см. рисунок 3). Заменяя r dr на r dr, получаем
 1 2 
Q
40
2
rdr
r
3

1
Q 1 1
  .
40  r1 r2 
Это означает, что разность потенциалов зависит только от
расстояний r1 и r2, на которых точки 1 и 2 находятся от заряда Q, и
не зависит от траектории, по которой происходит перемещения
заряда q из точки 1 в точку 2.
Рис. 3