Вариант III - Reshaem.Net

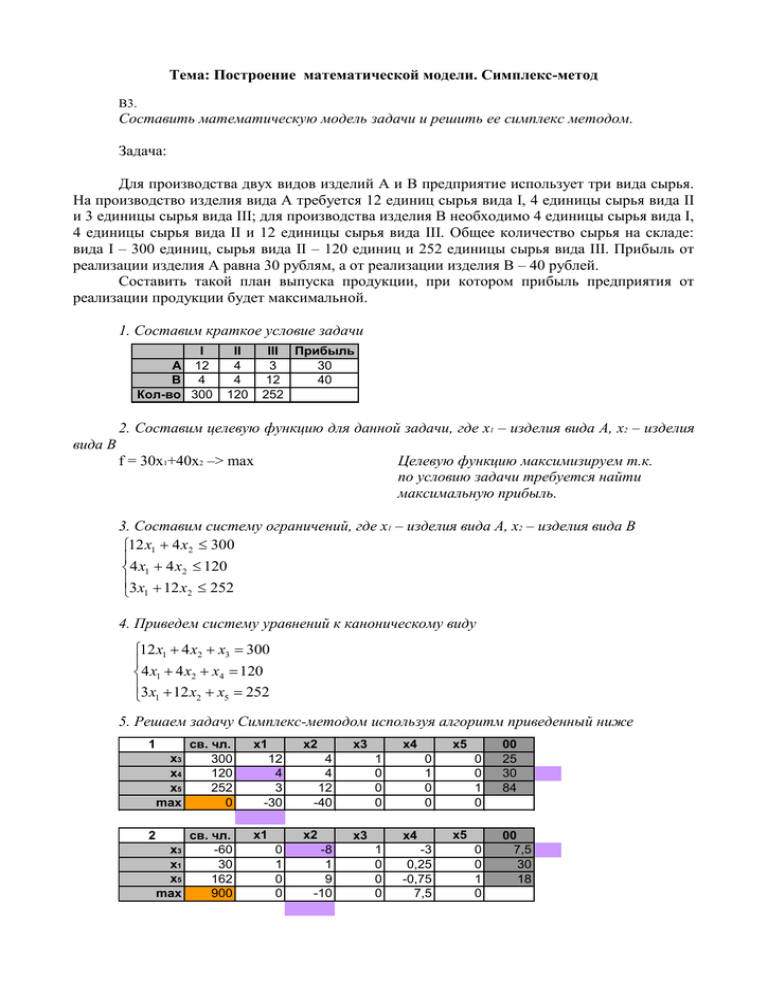
Тема: Построение математической модели. Симплекс-метод
В3.
Составить математическую модель задачи и решить ее симплекс методом.
Задача:
Для производства двух видов изделий А и В предприятие использует три вида сырья.
На производство изделия вида А требуется 12 единиц сырья вида I, 4 единицы сырья вида II
и 3 единицы сырья вида III; для производства изделия В необходимо 4 единицы сырья вида I,
4 единицы сырья вида II и 12 единицы сырья вида III. Общее количество сырья на складе:
вида I – 300 единиц, сырья вида II – 120 единиц и 252 единицы сырья вида III. Прибыль от
реализации изделия А равна 30 рублям, а от реализации изделия В – 40 рублей.
Составить такой план выпуска продукции, при котором прибыль предприятия от
реализации продукции будет максимальной.
1. Составим краткое условие задачи
I
A 12
B 4
Кол-во 300
II
4
4
120
III Прибыль
3
30
12
40
252
2. Составим целевую функцию для данной задачи, где x1 – изделия вида А, x2 – изделия
вида В
f = 30x1+40x2 –> max
Целевую функцию максимизируем т.к.
по условию задачи требуется найти
максимальную прибыль.
3. Составим систему ограничений, где x1 – изделия вида А, x2 – изделия вида В
12 x1  4 x2  300

4 x1  4 x2  120
3x  12 x  252
2
 1
4. Приведем систему уравнений к каноническому виду
12 x1  4 x2  x3  300

4 x1  4 x2  x4  120
3x  12 x  x  252
2
5
 1
5. Решаем задачу Симплекс-методом используя алгоритм приведенный ниже
св. чл.
300
120
252
0
x1
x3
x4
x5
max
св. чл.
-60
30
162
900
x1
x3
x1
x5
max
1
2
x2
12
4
3
-30
x2
0
1
0
0
x3
4
4
12
-40
-8
1
9
-10
x5
x4
1
0
0
0
x3
0
1
0
0
x4
1
0
0
0
-3
0,25
-0,75
7,5
0
0
1
0
x5
0
0
1
0
00
25
30
84
00
7,5
30
18
св. чл.
7,5
22,5
94,5
975
x1
x2
x1
x5
max
x1
x2
x1
x3
max
св. чл.
18
12
84
1080
3
4
Ответ:
x2
0
1
0
0
1
0
0
0
x2
0
1
0
0
x3
-0,125
0,125
1,125
-1,25
x3
1
0
0
0
0
0
1
0
x4
0,375
-0,125
-4,125
11,25
x5
0
0
1
0
x5
x4
-0,083 0,1111
0,3333 -0,111
-3,667 0,8889
6,6667 1,1111
00
**
180
84
00
Максимальная прибыль 1080;
Производство изделий вида А = 12, и В = 18;
Для производства изделий вида А затрачено материалов вида
I – 144, II – 48, III – 36
Для производства изделий вида В затрачено материалов вида
I – 72, II – 72, III – 216
Алгоритм решения задачи многомерной оптимизации Симплекс-методом.
1.
Проверяем, допустимо ли базовое решение (т.е. все ли bi≥0). Если один из
свободных членов bi
отрицательный, то строка i является «недопустимой» и
автоматически становится разрешающей. Ищем в ней отрицательные коэффициенты aij,
столбец с отрицательным коэффициентом делаем разрешающим. Если таких
коэффициентов нет – значит не существует ОДР, дальше можно не решать.
2.
Если базовое решение допустимо, проверяем оптимальность решения. При
максимизации целевой функции в соответствующей строке коэффициентов не должно
быть отрицательных элементов, при минимизации – положительных. Если решение не
оптимально, выбираем столбец с отрицательным (при fmax) или положительным (при fmin)
коэффициентом в качестве разрешающего.
3.
Вычисляем оценочные отношения по следующему правилу:


, если a ij и b i с разными знаками ;
, если a ij  0 , а b i  0;

OO  , если a ij  0;

0, если a ij  0 и b i  0;

b
иначе i .
a ij

4 x1  4 x2  120

3x1  12 x2  252
4.
Среди ОО выбираем наименьшее и соответствующая строка становится
разрешающей.
5.
Если все ОО равны бесконечности, это значит, что ОДР незамкнута и
функция улучшается в сторону незамкнутости. Оптимальное решение не существует.
ЗАДАНИЕ
(Решить 2-ую задачу так же как и первую, т.е. 1ая задача это пример(образец))
Составить математическую модель задачи и решить ее симплекс методом.
Задача 2. Три поставщика одного и того же продукта располагают в планируемый период следующими
его запасами: первый – 120 условных единиц, второй – 100 условных единиц, третий – 80 условных единиц.
Этот продукт должен быть перевезен к трем потребителям, потребности которых равны 90, 90 и 120 условных
единиц, соответственно. Стоимость перевозок от первого поставщика всем потребителям составляет $7, $6 и $4
соответственно, от второго поставщика – $3, $8 и $5, а от третьего – $2, $3 и $7. Необходимо определить
наиболее дешевый вариант перевозок, при этом каждый поставщик должен отправить столько груза, сколько
имеется у него в запасе, а каждый потребитель должен получить нужное ему количество продукции.
И еще... нужны объяснения к 1-ой задачи
Расписать подробнее на словах как мы получаем эту/эти таблицы и что обозначают
выделенные цифры, почему именно их выделяем (сиреневым и оранжевым)?
5. Решаем задачу Симплекс-методом используя алгоритм приведенный ниже
св. чл.
300
120
252
0
x1
x3
x4
x5
max
x1
x3
x1
x5
max
св. чл.
-60
30
162
900
1
2
x2
12
4
3
-30
x2
0
1
0
0
x3
4
4
12
-40
-8
1
9
-10
x5
x4
1
0
0
0
x3
0
1
0
0
x4
1
0
0
0
-3
0,25
-0,75
7,5
0
0
1
0
x5
0
0
1
0
00
25
30
84
00
7,5
30
18