Калинина А.Д., учитель математики ИСПОЛЬЗОВАНИЕ ТЕХНОЛОГИИ ДИАЛОГОВОЙ ВЗАИМОПОМОЩИ
реклама

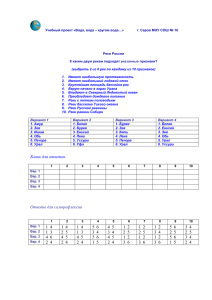
Калинина А.Д., учитель математики высшей квалификационной категории ИСПОЛЬЗОВАНИЕ ТЕХНОЛОГИИ ДИАЛОГОВОЙ ВЗАИМОПОМОЩИ НА УРОКАХ ГЕОМЕТРИИ Технология диалоговой взаимопомощи – одна из педагогических технологий, помогающая разрешить многие проблемы образования. При использовании технологии диалоговой взаимопомощи учащиеся общаются в динамических парах, каждый одновременно является и учащимся, и учителем, а это способствует усилению самостоятельности, раскрепощенности, умению видеть чужие трудности, а через это и свои преодолеть. Работа по этой технологии позволяет сделать изучение материала более интересным, творческим и, главное, - продуктивным. У учащихся раскрываются интеллектуальнотворческие и коммуникативные способности, происходит процесс единения коллектива на данный момент. Мною проведены два урока в 9м классе по теме «Векторы» с использованием технологии диалоговой взаимопомощи. Цель уроков: отработка практических умений и навыков на серии аналогичных задач, выявление качества и уровня овладения знаниями и умениями, полученными на предыдущих уроках. Так как векторам уделяется серьезное внимание и на уроках геометрии, и на уроках алгебры, то значимость этой темы очевидна. В ней охватывается широкий круг вопросов из других разделов, а именно: тождества сокращенного умножения, тригонометрические функции углов, вычислительные задачи, умение работать с арифметическими корнями. В ходе урока проговариваются теоретические положения, выполняется практическая работа. Проверочная самостоятельная работа позволяет выявить степень усвоения материала. Приведу пример заданий, которые были разработаны мною для урока геометрии в 9 классе по теме «Решение задач по теме «Координаты вектора»». Задания на карточках: Дано: а х1; у1 Дано: a x1; y1 b x2 ; y2 Найти: a , a b , координаты 2b Дано: А x1; y1 В x2 ; y2 С x3 ; y3 К - середина АВ Найти: СК, AB b x2 ; y2 Найти: a , a b , 3b Составляются по 8 карточек для более сильных учащихся и по 8 для средних учащихся. Остальным – карточки с образцами решения для работы в парах. I вар. II вар. III вар. а 2; 2 а 5; 2 а 3; 5 b 2; 5 а 6;3 IV вар. b 5; 2 V вар. b 5; 7 а 9; 4 VII вар. а 4;3 b 1; 7 b 7; 4 VI вар. а 8; 6 b 7;11 VIII вар. а 4; 3 b 8;7 b 2;6 I вариант А (4;-1) В (-2;3) С (-3;-3) II вариант III вариант IV вариант А (-3;5) А (-11;6) А (4;-9) В (-1;1) В (5;-8) В (-6;3) С (-3;-5) С (-3;-4) С (-2;-5) V вариант А (-6;3) В (4;-9) С (2;-5) VI вариант VII вариант VIII вариант А (5;-8) А (-1;1) А (-2;3) В (-11;6) В (-3;5) В (4;-1) С (-8;-9) С (5;2) С (-2;2) Ход урока: I Устная работа 1) Дано: а 2; 4 m3; 1 b 5;3 n 7;7 c 0; 7 f 2; 11 k 0; 21 s 25;15 Найти связь между а , b , c и остальными векторами. 2) Длина каких векторов найдена? 1. 4 16 20 2. 25 9 34 3. 7 3) Повторить формулы для нахождения координат середины отрезка, координат вектора по координатам его начала и конца. Дано: А (7;-4) Найти: а) Координаты К В (-8;5) б) AB К – середина АВ в) BA г) BA II Работа в парах по карточкам III Самостоятельная работа Найти a b , ВС, координаты KC по условию своего варианта. Домашнее задание: составить свой вариант работы и решить его На втором уроке рассматривалась тема «Скалярные произведения векторов». Серьезное внимание уделялось теоретической части. Каждый учащийся должен был по листу взаимопроверки проговорить правила отыскания конкретных значений: 1. Скалярный квадрат вектора 2. Длина вектора 3. Квадрат суммы двух векторов 4. Скалярное произведение двух векторов 5. Длина вектора через его координаты 6. Косинус угла между векторами Затем выполняется работа по карточкам. Приведу пример одного из вариантов таких карточек, которые были мною разработаны для урока. I вариант Дано: a 2 , b 1 , угол между векторами a и b равен Найти: a 3b , если =900, =1200 Задания для других вариантов составляются подобные. По данной технологии учащиеся после работы в парах выполняют самостоятельную работу диагностического характера. Анализ итогов работ учащихся после урока показал, что большая часть учащихся справилась с предложенными заданиями и получали положительные отметки, но в тоже время была определена группа учащихся, которые не смогли справиться с заданиями самостоятельной работы и требуют индивидуального подхода учителя. Таким образом, данный метод обучения учащихся выявил пробелы в знаниях учащихся и дал толчок для дальнейшей работы. На мой взгляд, использование технологии диалоговой взаимопомощи является очень целесообразным для работы учителя.