1. Компьютерный расчет полета камня, ... некоторым углом к горизонту, показал, что вначале расстояние до точки...

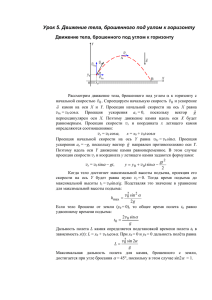
1. Компьютерный расчет полета камня, брошенного со скоростью 40 м/с под
некоторым углом к горизонту, показал, что вначале расстояние до точки броска
возрастало, через 5 секунд после броска стало максимальным, а дальше –
уменьшалось. Найти по этим данным максимальную высоту подъема камня над
уровнем точки броска. Ускорение при расчете принималось равным 10 м/с2,
сопротивление воздуха не учитывалось.
Решение:
ℎ=
(𝑣0 sin 𝑎)2
2𝑔
;
нам надо найти sin a;
В момент времени t=5 с, камень имеет координаты:
𝑥1 = 𝑣0 cos 𝑎 ∗ 𝑡;
𝑔𝑡 2
𝑦1 = 𝑣0 sin 𝑎 ∗ 𝑡 −
;
2
И проекции скоростей:
𝑣𝑥 = 𝑣0 cos 𝑎;
𝑣𝑦 = −(𝑣0 sin 𝑎 − 𝑔𝑡);
y
𝑣𝑥
y1
𝑣𝑦
𝑣
0
x1
x
Вектор перемещения из начала полета до максимально удаленной точки
перпендикулярен вектору скорости.
𝑐𝑡𝑔 𝑎 =
𝑥1
𝑦1
=
𝑣𝑦
𝑣𝑥
=
𝑣0 cos 𝑎∗𝑡
𝑣0 sin 𝑎∗𝑡−
𝑔𝑡2
=
2
Отсюда : sin 𝑎 =
ℎ=
(𝑣0
sin 𝑎)2
2𝑔
−(𝑣0 sin 𝑎−𝑔𝑡)
𝑣0 cos 𝑎;
285
300
= 0,95;
= 72.2 (м)
Ответ: 72.2 (м)
; 𝑣0 = 40 м/𝑐;
2. На листе бумаги с уменьшением в 10 раз нарисовали траекторию камня,
брошенного под углом 45º к поверхности земли со скоростью 20 м/с. По
нарисованной кривой ползет с неизменной по величине скоростью 0,02 м/с
маленький жучок. Чему равно ускорение жучка в точке, соответствующей
вершине траектории камня?
Решение.
𝑣𝑥
⃗⃗⃗⃗
𝑔
R
𝑣𝑥 = 𝑣0 ∗ cos 𝑎;
В верхней точке:
𝑔=
(𝑣0 ∗ cos 𝑎)2
;
𝑅
Отсюда : 𝑅 = 20 (м);
Радиус на чертеже 𝑅 ′ =
𝑎=
𝑣ж2
𝑅′
𝑅
10
= 2(м)
= 0,0002(м/𝑐 2 );
Ответ: 0,0002(м/𝑐 2 )
4. Азот вначале нагревают, затем охлаждают – так, что от начального состояния p1
= 0,5 атм, V1 = 30 л до конечного p2 = 0,5 атм, V2 = 50 л график процесса на
диаграмме pV представляет собой половину окружности (одна «клетка» по
вертикальной оси равна 0,1 атм, «клетка» по горизонтали составляет 10 литров).
Какую работу совершает газ в этом процессе?
Решение.
По закону Бойля-Мариотта:
(𝑃𝑉)𝑚𝑎𝑥 = (40 +
10
) ∗ (0,5 +
0,1
) = 26,86957
√2
√2
𝑃𝑚𝑎𝑥 + 𝑃1
0,5707106 + 0,5
𝐴=
∗ (𝑉2 − 𝑉1 ) =
∗ 105 ∗ (50 − 30) ∗
2
2
∗ 10−3 = 1070,71 (Дж )
Ответ:1070,71 Дж
6. Нелинейный
двухполюсник
имеет
«квадратичную»
вольтамперную
характеристику – напряжение между его выводами пропорционально квадрату
текущего
через
него
тока.
Двухполюсник
подключают
к
батарейке
напряжением U последовательно с вольтметром, при этом вольтметр
показывает половину напряжения батарейки. Параллельно двухполюснику
подключают еще один такой же вольтметр. Найти показания вольтметров.
Внутреннее сопротивление батарейки считать малым.
Решение:
При первом включении в цепи сила тока I, напряжение на вольтметре 𝑈𝑣1 :
𝑈𝑣1 =
𝑢
;
2
После подключения второго вольтметра:
𝐼2 = 𝑘𝐼;
Напряжение и сила тока на параллельном вольтметре:
𝑈𝑣2
𝑘2𝑢
=
;
2
𝐼𝑣2 = 𝑘 2 𝐼;
Напряжение на первом вольтметре:
𝑈𝑣2(1)
𝑘2𝑢 𝑢
=𝑈−
= (2 − 𝑘 2 );
2
2
т. е. увеличилось в (2 − 𝑘 2 ) раз.
Ток через него течет суммарный:
𝐼𝑣2 = (2 − 𝑘 2 )𝐼 = 𝑘𝐼 + 𝑘 2 𝐼;
(2 − 𝑘 2 ) = 𝑘 + 𝑘 2 ;
𝑘=
−1 + √17
;
4
𝑈𝑣2 =
𝑈𝑣2(1) =
𝑘2𝑢
= 0.3𝑈;
2
𝑢
(2 − 𝑘 2 ) = 0.7𝑈;
2
Ответ: 0.7𝑈; 0.3𝑈