Статья №2. Кинематика.

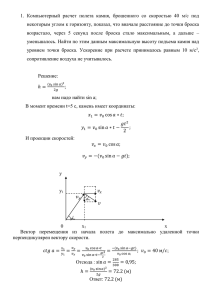
Дистанционная подготовка Abitu.ru
ФИЗИКА
Статья №2. Кинематика.
Теоретический материал.
В этой статье мы рассмотрим задачи на составление уравнений движения материальной точки в плоскости. Пусть
задана декартовая прямоугольная система координат.
Основные кинематические уравнения при равнопеременном прямолинейном движении точки:
Vx (t )  V0 x  ax  t
Vy (t )  V0 y  a y  t
a t2
x(t )  x0  V0 x  t  x
2
y (t )  y0  V0 y  t 
ay  t 2
2
(1)
x0 - начальная координата точки по оси абсцисс
y0 - начальная координата точки по оси ординат
V0 x - проекция начальной скорости точки на ось абсцисс
V0 y - проекция начальной скорости точки на ось ординат
Vx (t ) - проекция скорости точки на ось абсцисс в момент времени t
V y (t ) - проекция скорости точки на ось ординат в момент времени t
x(t ) - координата точки по оси абсцисс в момент времени t
y (t ) - координата точки по оси ординат в момент времени t
ax - проекция ускорения точки на ось абсцисс
a y - проекция ускорения точки на ось абсцисс
Основные кинематические уравнения при равномерном прямолинейном движении точки такие же как уравнения
(1), только слагаемые, содержащие проекции ускорения, отсутствуют.
Как применять уравнения (1) иллюстрируют примеры решения задач.
Примеры решения задач.
Пример 1.
Камень бросили с поверхности земли под углом β0 к горизонту. Начальная скорость камня равна V0.
Сопротивлением воздуха пренебречь.
1) Выбрать декартовую прямоугольную систему координат. Написать основные уравнения движения.
2) Вывести уравнение траектории камня. Убедится, что траекторией будет парабола, ветви которой направлены
вниз.
3) Определить время подъёма, время падения и время полёта камня.
4) Определить дальность полёта камня (двумя различными способами).
5) Определить максимальную высоту подъёма камня (двумя различными способами).
6) Найти зависимость скорости камня от времени.
Решение:
Поскольку сопротивлением воздуха пренебрегается, то на камень будет действовать только сила тяжести,
сообщающая камню ускорение (относительно земли), равное ускорению свободного падения g . Итак, полное
ускорение a камня равно g , направлено вертикально вниз, значит, по горизонтали движение камня будем
равномерным, а по вертикали – равнопеременным.
1) Выберем декартовую прямоугольную систему координат так, как показано на рисунке снизу. Пусть точка М –
камень, точка B – наивысшая точка траектории, точка А – точка падения камня на землю. Пусть H – максимальная
высота подъёма, L - дальность полёта. Движение проекции точки M по оси абсцисс является прямолинейным
равномерным. Движение проекции точки M на ось ординат является прямолинейным равнопеременным.
Основные кинематические уравнения движения:
x0  0, y0  0, V0 x  V0 cos  0 , V0 y  V0 sin  0 ;
ax (t )  0, a y (t )   g  const;
(1)
Vx (t )  V0 x  ax  t  V0 cos  0 ,
(2)
Vy (t )  V0 y  a y  t  V0 sin  0  gt ;
(3)
ax  t 2
 V0 cos  0  t ,
2
a t2
g  t2
y (t )  y0  V0 y  t  y
 V0 sin  0  t 
.
2
2
x(t )  x0  V0 x  t 
(4)
(5)
2) Из уравнения (4) выражаем t через x и подставляем в уравнение (5), получаем уравнение траектории камня:
y  x   x  tg 0 
g  x2
2V02 cos 2  0
(6)
Из (6) видим, что функция y ( x) является квадратичной, значит, графиком это функции является парабола.
Поскольку коэффициент при старшем члене квадратичной функции (6) отрицательный, то ветви этой параболы
L

;H  .
2

направлены вниз. Точка А имеет координаты  L;0  . Точка B имеет координаты 
3) Пусть t0 - время полёта камня, t1 - время подъёма камня, t2 - время падения камня.
Заметим, что y (t0 )  0 , значит, V0 sin  0  t0 
2V sin 0
g  t02
 0 , откуда t0  0
.
g
2
V0 sin 0
.
g
2V sin 0 V0 sin 0 V0 sin  0
V sin 0


Верно, что t0  t1  t2 , откуда t2  t0  t1  0
, т.е. t2  0
.
g
g
g
g
Отметим, что время подъёма камня равно времени падения камня ( t1  t2 ).
Заметим, что Vy (t1 )  0 (скорость горизонтальна), значит, V0 sin  0  gt1  0 , откуда t1 
4) Первый способ. Воспользуемся уравнением (4). Заметим, что x(t0 )  L , значит, L  V0 cos  0  t0 , , откуда
V02 sin 2 0
получаем L 
.
g
Второй способ. Воспользуемся уравнением (6). Заметим, что y  L   0 , значит, L  tg 0 
g  L2
 0 , откуда
2V02 cos 2  0
V02 sin 2 0
получаем L 
.
g
g  t12
5) Первый способ. Воспользуемся уравнением (5). Заметим, что y (t1 )  H , значит, H  V0 sin  0  t1 
, откуда
2
V 2 sin 2 0
g  t12
H  V0 sin 0  t1 
и H 0
.
2g
2
L
g  L2
L

H
,
значит,
,
H


tg



0
2
8V02 cos 2  0
2
Второй способ. Воспользуемся уравнением (6). Заметим, что y 
откуда H 
V02 sin 2 0
.
2g
2
6) Заметим, что V (t )  Vx2 (t )  V y2 (t ) , значит, V (t )  V02 cos 2  0  V0 sin 0  gt  .
Ответ:
см. решение.
Пример 2. [МФТИ 1981]
За последнюю секунду свободно падающее без начальной скорости тело пролетело 3/4 всего пути. Сколько
времени падало тело? Сопротивлением воздуха пренебречь.
Решение:
Выберем одномерную декартовую систему координат (см. рис. слева). Пусть y (t ) - координата
тела в момент времени t . Пусть t  0 - момент времени, когда отпустили тело без начальной
скорости. Тогда y (0)  H , где H – высота, с которой отпустили тело.
Обозначим за t0 - время, в течение которого тело падало с высоты H на землю. Тогда y (t0 )  0 .
По условию y (t0  t1 ) 
gt 2
3
H , где t1  1 c . Уравнение движения тела: y (t )  H 
.
4
2
3
g (t0  t1 )2
gt02
gt02
2
2
Итак, H  H 
, откуда H  2 g (t0  t1 ) . Т.к. y (t0 )  0 , то H 
, значит, 2 g (t0  t1 ) 
, откуда
4
2
2
2
t0  2t1  2 c .
Ответ:
2 секунды.
Пример 3. [МФТИ 1997]
Два камня брошены из одной точки над поверхностью земли с одинаковыми скоростями: один — вертикально
вверх, другой — вертикально вниз. Они упали на землю с интервалом времени t0. С какой скоростью были
брошены камни? Сопротивлением воздуха пренебречь.
Решение:
Выберем одномерную декартовую систему координат (см. рисунок). Пусть y1 (t ) - координата
первого тела в момент времени t . Пусть y2 (t ) - координата второго тела в момент времени t .
Пусть t  0 - момент времени, когда бросили тела. Тогда y1 (0)  y2 (0)  H , где H – высота, с
которой бросили тела. Пусть V0 - скорость, с которой были брошены тела. Обозначим за t1 время, через которого первое тело упало на землю. Обозначим за t2 - время, через которого
второе тело упало на землю. Тогда y1 (t1 )  0 и y2 (t2 )  0 . По условию t1  t2  t0 . Уравнение движения первого
gt 2
gt 2
тела: y1 (t )  H  V0t 
. Уравнение движения второго тела: y2 (t )  H  V0t 
.
2
2
gt 2
gt 2
gt 2
gt 2
Итак, H  V0t1  1  0 и H  V0t2  2  0 . Выражая H из обоих уравнений, получим 1  V0t1  V0t2  2 ,
2
2
2
2
значит,
Ответ:

g  t12  t2 2
2
  V  t
0
g  t0
.
2
2
 t1  , откуда
g   t1  t2 
2
 V0 , значит, V0 
g  t0
.
2
Пример 4. [Пенкин М.А.]
Шарик массой m=250 г бросают с поверхности земли под углом к горизонту так, что за t0=2 с он достигает
наибольшей высоты подъема, равной H=8 м . Во сколько раз и как изменится наибольшая высота подъема
шарика, если пренебречь сопротивлением воздуха? Силу сопротивления воздуха считать пропорциональной



скорости шарика: Fc=  kV , где V - скорость шарика, k=0,17 кг с – коэффициент пропорциональности.
Решение:
Пусть тело было брошено под углом  0 к горизонту с начальной
скоростью V0 . В отсутствие сопротивления воздуха максимальная
высота подъема тела равна nH=
V02 sin2 0
2g
, откуда n=
V02 sin2 0
2gH
.
Рассмотрим случай, когда есть сила сопротивления воздуха (см. рис.).
Второй закон Ньютона для тела в проекции на ось y:
may=m
Vy
t
=  Fc sin   mg (t  0) .
Т.к. Vy=V sin  , имеем m
Vy
t
=  kVy  mg ,
откуда mVy=  ky  mg  t . Суммируя почленно последнее уравнение
за время подъема t0 , получаем: m  (  V0sin0)=  kH  mgt0 , откуда V0sin 0= k H+gt0 .
m
2
Следовательно,
k

 m H+gt0 

 =4 раза .
n=
2gH
2
Ответ:
k

 m H+gt0 
 =4 раза .
увеличится в n= 
2gH
Домашнее задание.
Задача 1. Велосипедист, движущийся прямолинейно со скоростью 10 м/с, начинает равномерно уменьшать свою
скорость на 1 м/с каждую секунду и в итоге останавливается. Какой путь он пройдёт за последнюю секунду своего
движения?
Задача 2. Под каким углом к горизонту надо бросить тело, чтобы дальность его полёта была втрое больше
максимальной высоты его подъёма? Сопротивлением воздуха пренебречь.
Задача 3. Из миномёта ведут обстрел объекта, расположенного на плоском склоне горы
(рис.1). Угол наклона горы равен β, угол стрельбы по отношению к горизонту равен θ.
На каком расстоянии L=AB будут падать мины, если их начальная скорость равна V0?
Сопротивлением воздуха пренебречь. Решить задачу в двух различных декартовых
прямоугольных системах координат.
рис.1
Задача 4. Небольшой камень, брошенный с ровной горизонтальной поверхности земли под углом к горизонту,
упал обратно на землю в 19,6 м от места броска. Чему была равна скорость камня через 1 с после броска, если в
этот момент она была направлена горизонтально? Сопротивлением воздуха пренебречь.
Задача 5. [МФТИ 1989] С горизонтальной поверхности земли бросили мяч и он упал на землю со скоростью V0 под
углом β к горизонту. Модуль вертикальной составляющей скорости в точке бросания был на 20% больше, чем в
точке падения. Найти время полета мяча. Считать, что сила сопротивления движению мяча пропорциональна его
скорости.
16 сентября 2009 г.
Межвузовский центр воспитания и развития
талантливой молодежи в области
естественно-математических наук
"Физтех-центр"
Составители: Пенкин М.А., Шимко О.В., Шувалов Н.Д.
E-mail: [email protected], [email protected]
Сайт: www.abitu.ru